Public Member Functions | Static Public Member Functions | Public Attributes | Protected Types | Protected Member Functions | Protected Attributes | Static Protected Attributes | Private Member Functions | List of all members
libMesh::QMonomial Class Referencefinal

Implements quadrature rules for non-tensor polynomials. More...

#include <quadrature_monomial.h>

Inheritance diagram for libMesh::QMonomial:
Inheritance graph
[legend]

Public Member Functions

 QMonomial (unsigned int dim, Order order=INVALID_ORDER)
 
 QMonomial (const QMonomial &)=default
 
 QMonomial (QMonomial &&)=default
 
QMonomial & operator= (const QMonomial &)=default
 
QMonomial & operator= (QMonomial &&)=default
 
virtual ~QMonomial ()=default
 
virtual QuadratureType type () const override
 
ElemType get_elem_type () const
 
unsigned int get_p_level () const
 
unsigned int n_points () const
 
unsigned int get_dim () const
 
const std::vector< Point > & get_points () const
 
std::vector< Point > & get_points ()
 
const std::vector< Real > & get_weights () const
 
std::vector< Real > & get_weights ()
 
Point qp (const unsigned int i) const
 
Real w (const unsigned int i) const
 
virtual void init (const ElemType type=INVALID_ELEM, unsigned int p_level=0)
 
virtual void init (const Elem &elem, const std::vector< Real > &vertex_distance_func, unsigned int p_level=0)
 
Order get_order () const
 
void print_info (std::ostream &os=libMesh::out) const
 
void scale (std::pair< Real, Real > old_range, std::pair< Real, Real > new_range)
 
virtual bool shapes_need_reinit ()
 

Static Public Member Functions

static std::unique_ptr< QBase > build (const std::string &name, const unsigned int dim, const Order order=INVALID_ORDER)
 
static std::unique_ptr< QBase > build (const QuadratureType qt, const unsigned int dim, const Order order=INVALID_ORDER)
 
static void print_info (std::ostream &out=libMesh::out)
 
static std::string get_info ()
 
static unsigned int n_objects ()
 
static void enable_print_counter_info ()
 
static void disable_print_counter_info ()
 

Public Attributes

bool allow_rules_with_negative_weights
 

Protected Types

typedef std::map< std::string, std::pair< unsigned int, unsigned int > > Counts
 

Protected Member Functions

virtual void init_0D (const ElemType type=INVALID_ELEM, unsigned int p_level=0)
 
void tensor_product_quad (const QBase &q1D)
 
void tensor_product_hex (const QBase &q1D)
 
void tensor_product_prism (const QBase &q1D, const QBase &q2D)
 
void increment_constructor_count (const std::string &name)
 
void increment_destructor_count (const std::string &name)
 

Protected Attributes

unsigned int _dim
 
Order _order
 
ElemType _type
 
unsigned int _p_level
 
std::vector< Point > _points
 
std::vector< Real > _weights
 

Static Protected Attributes

static Counts _counts
 
static Threads::atomic< unsigned int > _n_objects
 
static Threads::spin_mutex _mutex
 
static bool _enable_print_counter = true
 

Private Member Functions

virtual void init_1D (const ElemType, unsigned int=0) override
 
virtual void init_2D (const ElemType _type=INVALID_ELEM, unsigned int p_level=0) override
 
virtual void init_3D (const ElemType _type=INVALID_ELEM, unsigned int p_level=0) override
 
void wissmann_rule (const Real rule_data[][3], const unsigned int n_pts)
 
void stroud_rule (const Real rule_data[][3], const unsigned int *rule_symmetry, const unsigned int n_pts)
 
void kim_rule (const Real rule_data[][4], const unsigned int *rule_id, const unsigned int n_pts)
 

Detailed Description

Implements quadrature rules for non-tensor polynomials.

This class defines alternate quadrature rules on "tensor-product" elements (quadrilaterals and hexahedra) which can be useful when integrating monomial finite element bases.

While tensor product rules are optimal for integrating bi/tri-linear, bi/tri-quadratic, etc. (i.e. tensor product) bases (which consist of incomplete polynomials up to degree=dim*p) they are not optimal for the MONOMIAL or FEXYZ bases, which consist of complete polynomials of degree=p.

This class provides quadrature rules which are more efficient than tensor product rules when they are available, and falls back on Gaussian quadrature rules otherwise.

A number of these rules have been helpfully collected in electronic form by: Prof. Ronald Cools Katholieke Universiteit Leuven, Dept. Computerwetenschappen http://www.cs.kuleuven.ac.be/~nines/research/ecf/ecf.html A username and password to access the tables is available by request.

We also provide the original reference for each rule when it is available.

Author
John W. Peterson
Date
2008

Definition at line 58 of file quadrature_monomial.h.

Member Typedef Documentation

◆ Counts

typedef std::map<std::string, std::pair<unsigned int, unsigned int> > libMesh::ReferenceCounter::Counts
protectedinherited

Data structure to log the information. The log is identified by the class name.

Definition at line 117 of file reference_counter.h.

Constructor & Destructor Documentation

◆ QMonomial() [1/3]

libMesh::QMonomial::QMonomial ( unsigned int  dim,
Order  order = INVALID_ORDER 
)
inline

Constructor. Declares the order of the quadrature rule.

Definition at line 65 of file quadrature_monomial.h.

66  :
67  QBase(dim,order)
68  {}
libMesh::QBase::QBase
QBase(unsigned int dim, Order order=INVALID_ORDER)
Definition: quadrature.h:364

◆ QMonomial() [2/3]

libMesh::QMonomial::QMonomial ( const QMonomial &  )
default

Copy/move ctor, copy/move assignment operator, and destructor are all explicitly defaulted for this simple class.

◆ QMonomial() [3/3]

libMesh::QMonomial::QMonomial ( QMonomial &&  )
default

◆ ~QMonomial()

virtual libMesh::QMonomial::~QMonomial ( )
virtualdefault

Member Function Documentation

◆ build() [1/2]

std::unique_ptr< QBase > libMesh::QBase::build ( const std::string &  name,
const unsigned int  dim,
const Order  order = INVALID_ORDER 
)
staticinherited

Builds a specific quadrature rule based on the name string. This enables selection of the quadrature rule at run-time. The input parameter name must be mappable through the Utility::string_to_enum<>() function.

This function allocates memory, therefore a std::unique_ptr<QBase> is returned so that the user does not accidentally leak it.

Definition at line 40 of file quadrature_build.C.

References libMesh::QBase::_dim, libMesh::QBase::_order, and libMesh::QBase::type().

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::attach_quadrature_rule().

43 {
44  return QBase::build (Utility::string_to_enum<QuadratureType> (type),
45  _dim,
46  _order);
47 }
libMesh::QBase::_dim
unsigned int _dim
Definition: quadrature.h:325
libMesh::QBase::type
virtual QuadratureType type() const =0
libMesh::QBase::build
static std::unique_ptr< QBase > build(const std::string &name, const unsigned int dim, const Order order=INVALID_ORDER)
Definition: quadrature_build.C:40

◆ build() [2/2]

std::unique_ptr< QBase > libMesh::QBase::build ( const QuadratureType  qt,
const unsigned int  dim,
const Order  order = INVALID_ORDER 
)
staticinherited

Builds a specific quadrature rule based on the QuadratureType. This enables selection of the quadrature rule at run-time.

This function allocates memory, therefore a std::unique_ptr<QBase> is returned so that the user does not accidentally leak it.

Definition at line 51 of file quadrature_build.C.

References libMesh::QBase::_dim, libMesh::QBase::_order, libMesh::FIRST, libMesh::FORTYTHIRD, libMesh::out, libMesh::QCLOUGH, libMesh::QCONICAL, libMesh::QGAUSS, libMesh::QGAUSS_LOBATTO, libMesh::QGRID, libMesh::QGRUNDMANN_MOLLER, libMesh::QJACOBI_1_0, libMesh::QJACOBI_2_0, libMesh::QMONOMIAL, libMesh::QSIMPSON, libMesh::QTRAP, libMesh::THIRD, and libMesh::TWENTYTHIRD.

54 {
55  switch (_qt)
56  {
57 
58  case QCLOUGH:
59  {
60 #ifdef DEBUG
61  if (_order > TWENTYTHIRD)
62  {
63  libMesh::out << "WARNING: Clough quadrature implemented" << std::endl
64  << " up to TWENTYTHIRD order." << std::endl;
65  }
66 #endif
67 
68  return libmesh_make_unique<QClough>(_dim, _order);
69  }
70 
71  case QGAUSS:
72  {
73 
74 #ifdef DEBUG
75  if (_order > FORTYTHIRD)
76  {
77  libMesh::out << "WARNING: Gauss quadrature implemented" << std::endl
78  << " up to FORTYTHIRD order." << std::endl;
79  }
80 #endif
81 
82  return libmesh_make_unique<QGauss>(_dim, _order);
83  }
84 
85  case QJACOBI_1_0:
86  {
87 
88 #ifdef DEBUG
89  if (_order > FORTYTHIRD)
90  {
91  libMesh::out << "WARNING: Jacobi(1,0) quadrature implemented" << std::endl
92  << " up to FORTYTHIRD order." << std::endl;
93  }
94 
95  if (_dim > 1)
96  {
97  libMesh::out << "WARNING: Jacobi(1,0) quadrature implemented" << std::endl
98  << " in 1D only." << std::endl;
99  }
100 #endif
101 
102  return libmesh_make_unique<QJacobi>(_dim, _order, 1, 0);
103  }
104 
105  case QJACOBI_2_0:
106  {
107 
108 #ifdef DEBUG
109  if (_order > FORTYTHIRD)
110  {
111  libMesh::out << "WARNING: Jacobi(2,0) quadrature implemented" << std::endl
112  << " up to FORTYTHIRD order." << std::endl;
113  }
114 
115  if (_dim > 1)
116  {
117  libMesh::out << "WARNING: Jacobi(2,0) quadrature implemented" << std::endl
118  << " in 1D only." << std::endl;
119  }
120 #endif
121 
122  return libmesh_make_unique<QJacobi>(_dim, _order, 2, 0);
123  }
124 
125  case QSIMPSON:
126  {
127 
128 #ifdef DEBUG
129  if (_order > THIRD)
130  {
131  libMesh::out << "WARNING: Simpson rule provides only" << std::endl
132  << " THIRD order!" << std::endl;
133  }
134 #endif
135 
136  return libmesh_make_unique<QSimpson>(_dim);
137  }
138 
139  case QTRAP:
140  {
141 
142 #ifdef DEBUG
143  if (_order > FIRST)
144  {
145  libMesh::out << "WARNING: Trapezoidal rule provides only" << std::endl
146  << " FIRST order!" << std::endl;
147  }
148 #endif
149 
150  return libmesh_make_unique<QTrap>(_dim);
151  }
152 
153  case QGRID:
154  return libmesh_make_unique<QGrid>(_dim, _order);
155 
156  case QGRUNDMANN_MOLLER:
157  return libmesh_make_unique<QGrundmann_Moller>(_dim, _order);
158 
159  case QMONOMIAL:
160  return libmesh_make_unique<QMonomial>(_dim, _order);
161 
162  case QGAUSS_LOBATTO:
163  return libmesh_make_unique<QGaussLobatto>(_dim, _order);
164 
165  case QCONICAL:
166  return libmesh_make_unique<QConical>(_dim, _order);
167 
168  default:
169  libmesh_error_msg("ERROR: Bad qt=" << _qt);
170  }
171 }
libMesh::QBase::_dim
unsigned int _dim
Definition: quadrature.h:325
libMesh::out
OStreamProxy out(std::cout)
Definition: libmesh_common.h:228

◆ disable_print_counter_info()

void libMesh::ReferenceCounter::disable_print_counter_info ( )
staticinherited

Definition at line 106 of file reference_counter.C.

References libMesh::ReferenceCounter::_enable_print_counter.

Referenced by libMesh::LibMeshInit::LibMeshInit().

107 {
108  _enable_print_counter = false;
109  return;
110 }

◆ enable_print_counter_info()

void libMesh::ReferenceCounter::enable_print_counter_info ( )
staticinherited

Methods to enable/disable the reference counter output from print_info()

Definition at line 100 of file reference_counter.C.

References libMesh::ReferenceCounter::_enable_print_counter.

101 {
102  _enable_print_counter = true;
103  return;
104 }

◆ get_dim()

unsigned int libMesh::QBase::get_dim ( ) const
inlineinherited
Returns
The spatial dimension of the quadrature rule.

Definition at line 136 of file quadrature.h.

References libMesh::QBase::_dim.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::attach_quadrature_rule(), libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), and libMesh::QConical::conical_product_tri().

136 { return _dim; }
libMesh::QBase::_dim
unsigned int _dim
Definition: quadrature.h:325

◆ get_elem_type()

ElemType libMesh::QBase::get_elem_type ( ) const
inlineinherited
Returns
The element type we're currently using.

Definition at line 117 of file quadrature.h.

References libMesh::QBase::_type.

117 { return _type; }
libMesh::QBase::_type
ElemType _type
Definition: quadrature.h:337

◆ get_info()

std::string libMesh::ReferenceCounter::get_info ( )
staticinherited

Gets a string containing the reference information.

Definition at line 47 of file reference_counter.C.

References libMesh::ReferenceCounter::_counts, and libMesh::Quality::name().

Referenced by libMesh::ReferenceCounter::print_info().

48 {
49 #if defined(LIBMESH_ENABLE_REFERENCE_COUNTING) && defined(DEBUG)
50 
51  std::ostringstream oss;
52 
53  oss << '\n'
54  << " ---------------------------------------------------------------------------- \n"
55  << "| Reference count information |\n"
56  << " ---------------------------------------------------------------------------- \n";
57 
58  for (const auto & pr : _counts)
59  {
60  const std::string name(pr.first);
61  const unsigned int creations = pr.second.first;
62  const unsigned int destructions = pr.second.second;
63 
64  oss << "| " << name << " reference count information:\n"
65  << "| Creations: " << creations << '\n'
66  << "| Destructions: " << destructions << '\n';
67  }
68 
69  oss << " ---------------------------------------------------------------------------- \n";
70 
71  return oss.str();
72 
73 #else
74 
75  return "";
76 
77 #endif
78 }
libMesh::Quality::name
std::string name(const ElemQuality q)
Definition: elem_quality.C:42

◆ get_order()

Order libMesh::QBase::get_order ( ) const
inlineinherited
Returns
The order of the quadrature rule.

Definition at line 203 of file quadrature.h.

References libMesh::QBase::_order, and libMesh::QBase::_p_level.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::attach_quadrature_rule().

203 { return static_cast<Order>(_order + _p_level); }
libMesh::QBase::_p_level
unsigned int _p_level
Definition: quadrature.h:343

◆ get_p_level()

unsigned int libMesh::QBase::get_p_level ( ) const
inlineinherited
Returns
The p-refinement level we're currently using.

Definition at line 122 of file quadrature.h.

References libMesh::QBase::_p_level.

122 { return _p_level; }
libMesh::QBase::_p_level
unsigned int _p_level
Definition: quadrature.h:343

◆ get_points() [1/2]

const std::vector<Point>& libMesh::QBase::get_points ( ) const
inlineinherited
Returns
A std::vector containing the quadrature point locations in reference element space.

Definition at line 142 of file quadrature.h.

References libMesh::QBase::_points.

Referenced by libMesh::QClough::init_1D(), libMesh::QConical::init_1D(), init_1D(), libMesh::QGrundmann_Moller::init_1D(), libMesh::QClough::init_2D(), libMesh::QGauss::init_2D(), init_2D(), libMesh::QGauss::init_3D(), and init_3D().

142 { return _points; }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349

◆ get_points() [2/2]

std::vector<Point>& libMesh::QBase::get_points ( )
inlineinherited
Returns
A std::vector containing the quadrature point locations in reference element space as a writable reference.

Definition at line 148 of file quadrature.h.

References libMesh::QBase::_points.

148 { return _points; }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349

◆ get_weights() [1/2]

const std::vector<Real>& libMesh::QBase::get_weights ( ) const
inlineinherited
Returns
A constant reference to a std::vector containing the quadrature weights.

Definition at line 154 of file quadrature.h.

References libMesh::QBase::_weights.

Referenced by libMesh::QClough::init_1D(), libMesh::QConical::init_1D(), init_1D(), libMesh::QGrundmann_Moller::init_1D(), libMesh::QClough::init_2D(), libMesh::QGauss::init_2D(), init_2D(), libMesh::QGauss::init_3D(), and init_3D().

154 { return _weights; }
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ get_weights() [2/2]

std::vector<Real>& libMesh::QBase::get_weights ( )
inlineinherited
Returns
A writable references to a std::vector containing the quadrature weights.

Definition at line 160 of file quadrature.h.

References libMesh::QBase::_weights.

160 { return _weights; }
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ increment_constructor_count()

void libMesh::ReferenceCounter::increment_constructor_count ( const std::string &  name)
inlineprotectedinherited

Increments the construction counter. Should be called in the constructor of any derived class that will be reference counted.

Definition at line 181 of file reference_counter.h.

References libMesh::ReferenceCounter::_counts, libMesh::Quality::name(), and libMesh::Threads::spin_mtx.

Referenced by libMesh::ReferenceCountedObject< RBParametrized >::ReferenceCountedObject().

182 {
183  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
184  std::pair<unsigned int, unsigned int> & p = _counts[name];
185 
186  p.first++;
187 }
libMesh::Quality::name
std::string name(const ElemQuality q)
Definition: elem_quality.C:42
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29

◆ increment_destructor_count()

void libMesh::ReferenceCounter::increment_destructor_count ( const std::string &  name)
inlineprotectedinherited

Increments the destruction counter. Should be called in the destructor of any derived class that will be reference counted.

Definition at line 194 of file reference_counter.h.

References libMesh::ReferenceCounter::_counts, libMesh::Quality::name(), and libMesh::Threads::spin_mtx.

Referenced by libMesh::ReferenceCountedObject< RBParametrized >::~ReferenceCountedObject().

195 {
196  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
197  std::pair<unsigned int, unsigned int> & p = _counts[name];
198 
199  p.second++;
200 }
libMesh::Quality::name
std::string name(const ElemQuality q)
Definition: elem_quality.C:42
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29

◆ init() [1/2]

void libMesh::QBase::init ( const ElemType  type = INVALID_ELEM,
unsigned int  p_level = 0 
)
virtualinherited

Initializes the data structures for a quadrature rule for an element of type type.

Definition at line 28 of file quadrature.C.

References libMesh::QBase::_dim, libMesh::QBase::_p_level, libMesh::QBase::_type, libMesh::QBase::init_0D(), libMesh::QBase::init_1D(), libMesh::QBase::init_2D(), and libMesh::QBase::init_3D().

Referenced by libMesh::QBase::init(), libMesh::QClough::init_1D(), init_1D(), libMesh::QClough::init_2D(), libMesh::QGaussLobatto::init_2D(), libMesh::QGrid::init_2D(), libMesh::QTrap::init_2D(), libMesh::QSimpson::init_2D(), libMesh::QGauss::init_2D(), init_2D(), libMesh::QGaussLobatto::init_3D(), libMesh::QTrap::init_3D(), libMesh::QGrid::init_3D(), libMesh::QSimpson::init_3D(), libMesh::QGauss::init_3D(), init_3D(), libMesh::QGauss::QGauss(), libMesh::QGaussLobatto::QGaussLobatto(), libMesh::QJacobi::QJacobi(), libMesh::QSimpson::QSimpson(), and libMesh::QTrap::QTrap().

30 {
31  // check to see if we have already
32  // done the work for this quadrature rule
33  if (t == _type && p == _p_level)
34  return;
35  else
36  {
37  _type = t;
38  _p_level = p;
39  }
40 
41 
42 
43  switch(_dim)
44  {
45  case 0:
46  this->init_0D(_type,_p_level);
47 
48  return;
49 
50  case 1:
51  this->init_1D(_type,_p_level);
52 
53  return;
54 
55  case 2:
56  this->init_2D(_type,_p_level);
57 
58  return;
59 
60  case 3:
61  this->init_3D(_type,_p_level);
62 
63  return;
64 
65  default:
66  libmesh_error_msg("Invalid dimension _dim = " << _dim);
67  }
68 }
libMesh::QBase::_type
ElemType _type
Definition: quadrature.h:337
libMesh::QBase::_dim
unsigned int _dim
Definition: quadrature.h:325
libMesh::QBase::_p_level
unsigned int _p_level
Definition: quadrature.h:343
libMesh::QBase::init_2D
virtual void init_2D(const ElemType, unsigned int=0)
Definition: quadrature.h:277
libMesh::QBase::init_1D
virtual void init_1D(const ElemType type=INVALID_ELEM, unsigned int p_level=0)=0
libMesh::QBase::init_0D
virtual void init_0D(const ElemType type=INVALID_ELEM, unsigned int p_level=0)
Definition: quadrature.C:82
libMesh::QBase::init_3D
virtual void init_3D(const ElemType, unsigned int=0)
Definition: quadrature.h:293

◆ init() [2/2]

void libMesh::QBase::init ( const Elem &  elem,
const std::vector< Real > &  vertex_distance_func,
unsigned int  p_level = 0 
)
virtualinherited

Initializes the data structures for an element potentially "cut" by a signed distance function. The array vertex_distance_func contains vertex values of the signed distance function. If the signed distance function changes sign on the vertices, then the element is considered to be cut.) This interface can be extended by derived classes in order to subdivide the element and construct a composite quadrature rule.

Definition at line 72 of file quadrature.C.

References libMesh::QBase::init(), and libMesh::Elem::type().

75 {
76  // dispatch generic implementation
77  this->init(elem.type(), p_level);
78 }
libMesh::QBase::init
virtual void init(const ElemType type=INVALID_ELEM, unsigned int p_level=0)
Definition: quadrature.C:28

◆ init_0D()

void libMesh::QBase::init_0D ( const ElemType  type = INVALID_ELEM,
unsigned int  p_level = 0 
)
protectedvirtualinherited

Initializes the 0D quadrature rule by filling the points and weights vectors with the appropriate values. Generally this is just one point with weight 1.

Definition at line 82 of file quadrature.C.

References libMesh::QBase::_points, and libMesh::QBase::_weights.

Referenced by libMesh::QBase::init().

84 {
85  _points.resize(1);
86  _weights.resize(1);
87  _points[0] = Point(0.);
88  _weights[0] = 1.0;
89 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ init_1D()

void libMesh::QMonomial::init_1D ( const ElemType  _elemtype,
unsigned int  p = 0 
)
overrideprivatevirtual

Just uses a Gauss rule in 1D.

Implements libMesh::QBase.

Definition at line 29 of file quadrature_monomial_1D.C.

References libMesh::QBase::_order, libMesh::QBase::_points, libMesh::QBase::_weights, libMesh::QBase::get_points(), libMesh::QBase::get_weights(), and libMesh::QBase::init().

31 {
32  QGauss gauss_rule(1, _order);
33  gauss_rule.init(_elemtype, p);
34 
35  _points.swap(gauss_rule.get_points());
36  _weights.swap(gauss_rule.get_weights());
37 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ init_2D()

void libMesh::QMonomial::init_2D ( const ElemType  _type = INVALID_ELEM,
unsigned int  p_level = 0 
)
overrideprivatevirtual

More efficient rules for quadrilaterals.

Reimplemented from libMesh::QBase.

Definition at line 28 of file quadrature_monomial_2D.C.

References libMesh::QBase::_order, libMesh::QBase::_points, libMesh::QBase::_weights, data, libMesh::EIGHTH, libMesh::ELEVENTH, libMesh::FIFTEENTH, libMesh::FIFTH, libMesh::FOURTEENTH, libMesh::FOURTH, libMesh::QBase::get_points(), libMesh::QBase::get_weights(), libMesh::QBase::init(), libMesh::NINTH, libMesh::QUAD4, libMesh::QUAD8, libMesh::QUAD9, libMesh::QUADSHELL4, libMesh::QUADSHELL8, libMesh::Real, libMesh::SECOND, libMesh::SEVENTEENTH, libMesh::SEVENTH, libMesh::SIXTEENTH, libMesh::SIXTH, stroud_rule(), libMesh::TENTH, libMesh::THIRTEENTH, libMesh::TWELFTH, and wissmann_rule().

30 {
31 
32  switch (type_in)
33  {
34  //---------------------------------------------
35  // Quadrilateral quadrature rules
36  case QUAD4:
37  case QUADSHELL4:
38  case QUAD8:
39  case QUADSHELL8:
40  case QUAD9:
41  {
42  switch(_order + 2*p)
43  {
44  case SECOND:
45  {
46  // A degree=2 rule for the QUAD with 3 points.
47  // A tensor product degree-2 Gauss would have 4 points.
48  // This rule (or a variation on it) is probably available in
49  //
50  // A.H. Stroud, Approximate calculation of multiple integrals,
51  // Prentice-Hall, Englewood Cliffs, N.J., 1971.
52  //
53  // though I have never actually seen a reference for it.
54  // Luckily it's fairly easy to derive, which is what I've done
55  // here [JWP].
56  const Real
57  s=std::sqrt(Real(1)/3),
58  t=std::sqrt(Real(2)/3);
59 
60  const Real data[2][3] =
61  {
62  {0.0, s, 2.0},
63  { t, -s, 1.0}
64  };
65 
66  _points.resize(3);
67  _weights.resize(3);
68 
69  wissmann_rule(data, 2);
70 
71  return;
72  } // end case SECOND
73 
74 
75 
76  // For third-order, fall through to default case, use 2x2 Gauss product rule.
77  // case THIRD:
78  // {
79  // } // end case THIRD
80 
81  // Tabulated-in-double-precision rules aren't accurate enough for
82  // higher precision, so fall back on Gauss
83 #if !defined(LIBMESH_DEFAULT_TRIPLE_PRECISION) && !defined(LIBMESH_DEFAULT_QUADRUPLE_PRECISION)
84  case FOURTH:
85  {
86  // A pair of degree=4 rules for the QUAD "C2" due to
87  // Wissmann and Becker. These rules both have six points.
88  // A tensor product degree-4 Gauss would have 9 points.
89  //
90  // J. W. Wissmann and T. Becker, Partially symmetric cubature
91  // formulas for even degrees of exactness, SIAM J. Numer. Anal. 23
92  // (1986), 676--685.
93  const Real data[4][3] =
94  {
95  // First of 2 degree-4 rules given by Wissmann
96  {Real(0.0000000000000000e+00), Real(0.0000000000000000e+00), Real(1.1428571428571428e+00)},
97  {Real(0.0000000000000000e+00), Real(9.6609178307929590e-01), Real(4.3956043956043956e-01)},
98  {Real(8.5191465330460049e-01), Real(4.5560372783619284e-01), Real(5.6607220700753210e-01)},
99  {Real(6.3091278897675402e-01), Real(-7.3162995157313452e-01), Real(6.4271900178367668e-01)}
100  //
101  // Second of 2 degree-4 rules given by Wissmann. These both
102  // yield 4th-order accurate rules, I just chose the one that
103  // happened to contain the origin.
104  // {0.000000000000000, -0.356822089773090, 1.286412084888852},
105  // {0.000000000000000, 0.934172358962716, 0.491365692888926},
106  // {0.774596669241483, 0.390885162530071, 0.761883709085613},
107  // {0.774596669241483, -0.852765377881771, 0.349227402025498}
108  };
109 
110  _points.resize(6);
111  _weights.resize(6);
112 
113  wissmann_rule(data, 4);
114 
115  return;
116  } // end case FOURTH
117 #endif
118 
119 
120 
121 
122  case FIFTH:
123  {
124  // A degree 5, 7-point rule due to Stroud.
125  //
126  // A.H. Stroud, Approximate calculation of multiple integrals,
127  // Prentice-Hall, Englewood Cliffs, N.J., 1971.
128  //
129  // This rule is provably minimal in the number of points.
130  // A tensor-product rule accurate for "bi-quintic" polynomials would have 9 points.
131  const Real data[3][3] =
132  {
133  { 0.L, 0.L, Real(8)/7 }, // 1
134  { 0.L, std::sqrt(Real(14)/15), Real(20)/63}, // 2
135  {std::sqrt(Real(3)/5), std::sqrt(Real(1)/3), Real(20)/36} // 4
136  };
137 
138  const unsigned int symmetry[3] = {
139  0, // Origin
140  7, // Central Symmetry
141  6 // Rectangular
142  };
143 
144  _points.resize (7);
145  _weights.resize(7);
146 
147  stroud_rule(data, symmetry, 3);
148 
149  return;
150  } // end case FIFTH
151 
152 
153 
154 
155  // Tabulated-in-double-precision rules aren't accurate enough for
156  // higher precision, so fall back on Gauss
157 #if !defined(LIBMESH_DEFAULT_TRIPLE_PRECISION) && !defined(LIBMESH_DEFAULT_QUADRUPLE_PRECISION)
158  case SIXTH:
159  {
160  // A pair of degree=6 rules for the QUAD "C2" due to
161  // Wissmann and Becker. These rules both have 10 points.
162  // A tensor product degree-6 Gauss would have 16 points.
163  //
164  // J. W. Wissmann and T. Becker, Partially symmetric cubature
165  // formulas for even degrees of exactness, SIAM J. Numer. Anal. 23
166  // (1986), 676--685.
167  const Real data[6][3] =
168  {
169  // First of 2 degree-6, 10 point rules given by Wissmann
170  // {0.000000000000000, 0.836405633697626, 0.455343245714174},
171  // {0.000000000000000, -0.357460165391307, 0.827395973202966},
172  // {0.888764014654765, 0.872101531193131, 0.144000884599645},
173  // {0.604857639464685, 0.305985162155427, 0.668259104262665},
174  // {0.955447506641064, -0.410270899466658, 0.225474004890679},
175  // {0.565459993438754, -0.872869311156879, 0.320896396788441}
176  //
177  // Second of 2 degree-6, 10 point rules given by Wissmann.
178  // Either of these will work, I just chose the one with points
179  // slightly further into the element interior.
180  {Real(0.0000000000000000e+00), Real(8.6983337525005900e-01), Real(3.9275059096434794e-01)},
181  {Real(0.0000000000000000e+00), Real(-4.7940635161211124e-01), Real(7.5476288124261053e-01)},
182  {Real(8.6374282634615388e-01), Real(8.0283751620765670e-01), Real(2.0616605058827902e-01)},
183  {Real(5.1869052139258234e-01), Real(2.6214366550805818e-01), Real(6.8999213848986375e-01)},
184  {Real(9.3397254497284950e-01), Real(-3.6309658314806653e-01), Real(2.6051748873231697e-01)},
185  {Real(6.0897753601635630e-01), Real(-8.9660863276245265e-01), Real(2.6956758608606100e-01)}
186  };
187 
188  _points.resize(10);
189  _weights.resize(10);
190 
191  wissmann_rule(data, 6);
192 
193  return;
194  } // end case SIXTH
195 #endif
196 
197 
198 
199 
200  case SEVENTH:
201  {
202  // A degree 7, 12-point rule due to Tyler, can be found in Stroud's book
203  //
204  // A.H. Stroud, Approximate calculation of multiple integrals,
205  // Prentice-Hall, Englewood Cliffs, N.J., 1971.
206  //
207  // This rule is fully-symmetric and provably minimal in the number of points.
208  // A tensor-product rule accurate for "bi-septic" polynomials would have 16 points.
209  const Real
210  r = std::sqrt(Real(6)/7),
211  s = std::sqrt( (114 - 3*std::sqrt(Real(583))) / 287 ),
212  t = std::sqrt( (114 + 3*std::sqrt(Real(583))) / 287 ),
213  B1 = Real(196)/810,
214  B2 = 4 * (178981 + 2769*std::sqrt(Real(583))) / 1888920,
215  B3 = 4 * (178981 - 2769*std::sqrt(Real(583))) / 1888920;
216 
217  const Real data[3][3] =
218  {
219  {r, 0.0, B1}, // 4
220  {s, 0.0, B2}, // 4
221  {t, 0.0, B3} // 4
222  };
223 
224  const unsigned int symmetry[3] = {
225  3, // Full Symmetry, (x,0)
226  2, // Full Symmetry, (x,x)
227  2 // Full Symmetry, (x,x)
228  };
229 
230  _points.resize (12);
231  _weights.resize(12);
232 
233  stroud_rule(data, symmetry, 3);
234 
235  return;
236  } // end case SEVENTH
237 
238 
239 
240 
241  // Tabulated-in-double-precision rules aren't accurate enough for
242  // higher precision, so fall back on Gauss
243 #if !defined(LIBMESH_DEFAULT_TRIPLE_PRECISION) && !defined(LIBMESH_DEFAULT_QUADRUPLE_PRECISION)
244  case EIGHTH:
245  {
246  // A pair of degree=8 rules for the QUAD "C2" due to
247  // Wissmann and Becker. These rules both have 16 points.
248  // A tensor product degree-6 Gauss would have 25 points.
249  //
250  // J. W. Wissmann and T. Becker, Partially symmetric cubature
251  // formulas for even degrees of exactness, SIAM J. Numer. Anal. 23
252  // (1986), 676--685.
253  const Real data[10][3] =
254  {
255  // First of 2 degree-8, 16 point rules given by Wissmann
256  // {0.000000000000000, 0.000000000000000, 0.055364705621440},
257  // {0.000000000000000, 0.757629177660505, 0.404389368726076},
258  // {0.000000000000000, -0.236871842255702, 0.533546604952635},
259  // {0.000000000000000, -0.989717929044527, 0.117054188786739},
260  // {0.639091304900370, 0.950520955645667, 0.125614417613747},
261  // {0.937069076924990, 0.663882736885633, 0.136544584733588},
262  // {0.537083530541494, 0.304210681724104, 0.483408479211257},
263  // {0.887188506449625, -0.236496718536120, 0.252528506429544},
264  // {0.494698820670197, -0.698953476086564, 0.361262323882172},
265  // {0.897495818279768, -0.900390774211580, 0.085464254086247}
266  //
267  // Second of 2 degree-8, 16 point rules given by Wissmann.
268  // Either of these will work, I just chose the one with points
269  // further into the element interior.
270  {Real(0.0000000000000000e+00), Real(6.5956013196034176e-01), Real(4.5027677630559029e-01)},
271  {Real(0.0000000000000000e+00), Real(-9.4914292304312538e-01), Real(1.6657042677781274e-01)},
272  {Real(9.5250946607156228e-01), Real(7.6505181955768362e-01), Real(9.8869459933431422e-02)},
273  {Real(5.3232745407420624e-01), Real(9.3697598108841598e-01), Real(1.5369674714081197e-01)},
274  {Real(6.8473629795173504e-01), Real(3.3365671773574759e-01), Real(3.9668697607290278e-01)},
275  {Real(2.3314324080140552e-01), Real(-7.9583272377396852e-02), Real(3.5201436794569501e-01)},
276  {Real(9.2768331930611748e-01), Real(-2.7224008061253425e-01), Real(1.8958905457779799e-01)},
277  {Real(4.5312068740374942e-01), Real(-6.1373535339802760e-01), Real(3.7510100114758727e-01)},
278  {Real(8.3750364042281223e-01), Real(-8.8847765053597136e-01), Real(1.2561879164007201e-01)}
279  };
280 
281  _points.resize(16);
282  _weights.resize(16);
283 
284  wissmann_rule(data, /*10*/ 9);
285 
286  return;
287  } // end case EIGHTH
288 
289 
290 
291 
292  case NINTH:
293  {
294  // A degree 9, 17-point rule due to Moller.
295  //
296  // H.M. Moller, Kubaturformeln mit minimaler Knotenzahl,
297  // Numer. Math. 25 (1976), 185--200.
298  //
299  // This rule is provably minimal in the number of points.
300  // A tensor-product rule accurate for "bi-ninth" degree polynomials would have 25 points.
301  const Real data[5][3] =
302  {
303  {Real(0.0000000000000000e+00), Real(0.0000000000000000e+00), Real(5.2674897119341563e-01)}, // 1
304  {Real(6.3068011973166885e-01), Real(9.6884996636197772e-01), Real(8.8879378170198706e-02)}, // 4
305  {Real(9.2796164595956966e-01), Real(7.5027709997890053e-01), Real(1.1209960212959648e-01)}, // 4
306  {Real(4.5333982113564719e-01), Real(5.2373582021442933e-01), Real(3.9828243926207009e-01)}, // 4
307  {Real(8.5261572933366230e-01), Real(7.6208328192617173e-02), Real(2.6905133763978080e-01)} // 4
308  };
309 
310  const unsigned int symmetry[5] = {
311  0, // Single point
312  4, // Rotational Invariant
313  4, // Rotational Invariant
314  4, // Rotational Invariant
315  4 // Rotational Invariant
316  };
317 
318  _points.resize (17);
319  _weights.resize(17);
320 
321  stroud_rule(data, symmetry, 5);
322 
323  return;
324  } // end case NINTH
325 
326 
327 
328 
329  case TENTH:
330  case ELEVENTH:
331  {
332  // A degree 11, 24-point rule due to Cools and Haegemans.
333  //
334  // R. Cools and A. Haegemans, Another step forward in searching for
335  // cubature formulae with a minimal number of knots for the square,
336  // Computing 40 (1988), 139--146.
337  //
338  // P. Verlinden and R. Cools, The algebraic construction of a minimal
339  // cubature formula of degree 11 for the square, Cubature Formulas
340  // and their Applications (Russian) (Krasnoyarsk) (M.V. Noskov, ed.),
341  // 1994, pp. 13--23.
342  //
343  // This rule is provably minimal in the number of points.
344  // A tensor-product rule accurate for "bi-tenth" or "bi-eleventh" degree polynomials would have 36 points.
345  const Real data[6][3] =
346  {
347  {Real(6.9807610454956756e-01), Real(9.8263922354085547e-01), Real(4.8020763350723814e-02)}, // 4
348  {Real(9.3948638281673690e-01), Real(8.2577583590296393e-01), Real(6.6071329164550595e-02)}, // 4
349  {Real(9.5353952820153201e-01), Real(1.8858613871864195e-01), Real(9.7386777358668164e-02)}, // 4
350  {Real(3.1562343291525419e-01), Real(8.1252054830481310e-01), Real(2.1173634999894860e-01)}, // 4
351  {Real(7.1200191307533630e-01), Real(5.2532025036454776e-01), Real(2.2562606172886338e-01)}, // 4
352  {Real(4.2484724884866925e-01), Real(4.1658071912022368e-02), Real(3.5115871839824543e-01)} // 4
353  };
354 
355  const unsigned int symmetry[6] = {
356  4, // Rotational Invariant
357  4, // Rotational Invariant
358  4, // Rotational Invariant
359  4, // Rotational Invariant
360  4, // Rotational Invariant
361  4 // Rotational Invariant
362  };
363 
364  _points.resize (24);
365  _weights.resize(24);
366 
367  stroud_rule(data, symmetry, 6);
368 
369  return;
370  } // end case TENTH,ELEVENTH
371 
372 
373 
374 
375  case TWELFTH:
376  case THIRTEENTH:
377  {
378  // A degree 13, 33-point rule due to Cools and Haegemans.
379  //
380  // R. Cools and A. Haegemans, Another step forward in searching for
381  // cubature formulae with a minimal number of knots for the square,
382  // Computing 40 (1988), 139--146.
383  //
384  // A tensor-product rule accurate for "bi-12" or "bi-13" degree polynomials would have 49 points.
385  const Real data[9][3] =
386  {
387  {Real(0.0000000000000000e+00), Real(0.0000000000000000e+00), Real(3.0038211543122536e-01)}, // 1
388  {Real(9.8348668243987226e-01), Real(7.7880971155441942e-01), Real(2.9991838864499131e-02)}, // 4
389  {Real(8.5955600564163892e-01), Real(9.5729769978630736e-01), Real(3.8174421317083669e-02)}, // 4
390  {Real(9.5892517028753485e-01), Real(1.3818345986246535e-01), Real(6.0424923817749980e-02)}, // 4
391  {Real(3.9073621612946100e-01), Real(9.4132722587292523e-01), Real(7.7492738533105339e-02)}, // 4
392  {Real(8.5007667369974857e-01), Real(4.7580862521827590e-01), Real(1.1884466730059560e-01)}, // 4
393  {Real(6.4782163718701073e-01), Real(7.5580535657208143e-01), Real(1.2976355037000271e-01)}, // 4
394  {Real(7.0741508996444936e-02), Real(6.9625007849174941e-01), Real(2.1334158145718938e-01)}, // 4
395  {Real(4.0930456169403884e-01), Real(3.4271655604040678e-01), Real(2.5687074948196783e-01)} // 4
396  };
397 
398  const unsigned int symmetry[9] = {
399  0, // Single point
400  4, // Rotational Invariant
401  4, // Rotational Invariant
402  4, // Rotational Invariant
403  4, // Rotational Invariant
404  4, // Rotational Invariant
405  4, // Rotational Invariant
406  4, // Rotational Invariant
407  4 // Rotational Invariant
408  };
409 
410  _points.resize (33);
411  _weights.resize(33);
412 
413  stroud_rule(data, symmetry, 9);
414 
415  return;
416  } // end case TWELFTH,THIRTEENTH
417 
418 
419 
420 
421  case FOURTEENTH:
422  case FIFTEENTH:
423  {
424  // A degree-15, 48 point rule originally due to Rabinowitz and Richter,
425  // can be found in Cools' 1971 book.
426  //
427  // A.H. Stroud, Approximate calculation of multiple integrals,
428  // Prentice-Hall, Englewood Cliffs, N.J., 1971.
429  //
430  // The product Gauss rule for this order has 8^2=64 points.
431  const Real data[9][3] =
432  {
433  {Real(9.915377816777667e-01L), Real(0.0000000000000000e+00), Real(3.01245207981210e-02L)}, // 4
434  {Real(8.020163879230440e-01L), Real(0.0000000000000000e+00), Real(8.71146840209092e-02L)}, // 4
435  {Real(5.648674875232742e-01L), Real(0.0000000000000000e+00), Real(1.250080294351494e-01L)}, // 4
436  {Real(9.354392392539896e-01L), Real(0.0000000000000000e+00), Real(2.67651407861666e-02L)}, // 4
437  {Real(7.624563338825799e-01L), Real(0.0000000000000000e+00), Real(9.59651863624437e-02L)}, // 4
438  {Real(2.156164241427213e-01L), Real(0.0000000000000000e+00), Real(1.750832998343375e-01L)}, // 4
439  {Real(9.769662659711761e-01L), Real(6.684480048977932e-01L), Real(2.83136372033274e-02L)}, // 4
440  {Real(8.937128379503403e-01L), Real(3.735205277617582e-01L), Real(8.66414716025093e-02L)}, // 4
441  {Real(6.122485619312083e-01L), Real(4.078983303613935e-01L), Real(1.150144605755996e-01L)} // 4
442  };
443 
444  const unsigned int symmetry[9] = {
445  3, // Full Symmetry, (x,0)
446  3, // Full Symmetry, (x,0)
447  3, // Full Symmetry, (x,0)
448  2, // Full Symmetry, (x,x)
449  2, // Full Symmetry, (x,x)
450  2, // Full Symmetry, (x,x)
451  1, // Full Symmetry, (x,y)
452  1, // Full Symmetry, (x,y)
453  1, // Full Symmetry, (x,y)
454  };
455 
456  _points.resize (48);
457  _weights.resize(48);
458 
459  stroud_rule(data, symmetry, 9);
460 
461  return;
462  } // case FOURTEENTH, FIFTEENTH:
463 
464 
465 
466 
467  case SIXTEENTH:
468  case SEVENTEENTH:
469  {
470  // A degree 17, 60-point rule due to Cools and Haegemans.
471  //
472  // R. Cools and A. Haegemans, Another step forward in searching for
473  // cubature formulae with a minimal number of knots for the square,
474  // Computing 40 (1988), 139--146.
475  //
476  // A tensor-product rule accurate for "bi-14" or "bi-15" degree polynomials would have 64 points.
477  // A tensor-product rule accurate for "bi-16" or "bi-17" degree polynomials would have 81 points.
478  const Real data[10][3] =
479  {
480  {Real(9.8935307451260049e-01), Real(0.0000000000000000e+00), Real(2.0614915919990959e-02)}, // 4
481  {Real(3.7628520715797329e-01), Real(0.0000000000000000e+00), Real(1.2802571617990983e-01)}, // 4
482  {Real(9.7884827926223311e-01), Real(0.0000000000000000e+00), Real(5.5117395340318905e-03)}, // 4
483  {Real(8.8579472916411612e-01), Real(0.0000000000000000e+00), Real(3.9207712457141880e-02)}, // 4
484  {Real(1.7175612383834817e-01), Real(0.0000000000000000e+00), Real(7.6396945079863302e-02)}, // 4
485  {Real(5.9049927380600241e-01), Real(3.1950503663457394e-01), Real(1.4151372994997245e-01)}, // 8
486  {Real(7.9907913191686325e-01), Real(5.9797245192945738e-01), Real(8.3903279363797602e-02)}, // 8
487  {Real(8.0374396295874471e-01), Real(5.8344481776550529e-02), Real(6.0394163649684546e-02)}, // 8
488  {Real(9.3650627612749478e-01), Real(3.4738631616620267e-01), Real(5.7387752969212695e-02)}, // 8
489  {Real(9.8132117980545229e-01), Real(7.0600028779864611e-01), Real(2.1922559481863763e-02)}, // 8
490  };
491 
492  const unsigned int symmetry[10] = {
493  3, // Fully symmetric (x,0)
494  3, // Fully symmetric (x,0)
495  2, // Fully symmetric (x,x)
496  2, // Fully symmetric (x,x)
497  2, // Fully symmetric (x,x)
498  1, // Fully symmetric (x,y)
499  1, // Fully symmetric (x,y)
500  1, // Fully symmetric (x,y)
501  1, // Fully symmetric (x,y)
502  1 // Fully symmetric (x,y)
503  };
504 
505  _points.resize (60);
506  _weights.resize(60);
507 
508  stroud_rule(data, symmetry, 10);
509 
510  return;
511  } // end case FOURTEENTH through SEVENTEENTH
512 #endif
513 
514 
515 
516  // By default: construct and use a Gauss quadrature rule
517  default:
518  {
519  // Break out and fall down into the default: case for the
520  // outer switch statement.
521  break;
522  }
523 
524  } // end switch(_order + 2*p)
525  } // end case QUAD4/8/9
526 
527  libmesh_fallthrough();
528 
529  // By default: construct and use a Gauss quadrature rule
530  default:
531  {
532  QGauss gauss_rule(2, _order);
533  gauss_rule.init(type_in, p);
534 
535  // Swap points and weights with the about-to-be destroyed rule.
536  _points.swap (gauss_rule.get_points() );
537  _weights.swap(gauss_rule.get_weights());
538 
539  return;
540  }
541  } // end switch (type_in)
542 }
libMesh::QMonomial::wissmann_rule
void wissmann_rule(const Real rule_data[][3], const unsigned int n_pts)
Definition: quadrature_monomial.C:37
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355
libMesh::QMonomial::stroud_rule
void stroud_rule(const Real rule_data[][3], const unsigned int *rule_symmetry, const unsigned int n_pts)
Definition: quadrature_monomial.C:57
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
data
IterBase * data
Definition: variant_filter_iterator.h:337

◆ init_3D()

void libMesh::QMonomial::init_3D ( const ElemType  _type = INVALID_ELEM,
unsigned int  p_level = 0 
)
overrideprivatevirtual

More efficient rules for hexahedra.

Reimplemented from libMesh::QBase.

Definition at line 28 of file quadrature_monomial_3D.C.

References libMesh::QBase::_order, libMesh::QBase::_points, libMesh::QBase::_weights, A, libMesh::QBase::allow_rules_with_negative_weights, data, libMesh::EIGHTH, libMesh::FIFTH, libMesh::FOURTH, libMesh::QBase::get_points(), libMesh::QBase::get_weights(), libMesh::HEX20, libMesh::HEX27, libMesh::HEX8, libMesh::QBase::init(), kim_rule(), libMesh::Real, libMesh::SECOND, libMesh::SEVENTH, libMesh::SIXTH, and libMesh::THIRD.

30 {
31 
32  switch (type_in)
33  {
34  //---------------------------------------------
35  // Hex quadrature rules
36  case HEX8:
37  case HEX20:
38  case HEX27:
39  {
40  switch(_order + 2*p)
41  {
42 
43  // The CONSTANT/FIRST rule is the 1-point Gauss "product" rule...we fall
44  // through to the default case for this rule.
45 
46  case SECOND:
47  case THIRD:
48  {
49  // A degree 3, 6-point, "rotationally-symmetric" rule by
50  // Kim and Song, Comm. Korean Math. Soc vol. 13, no. 4, 1998, pp. 913-931.
51  //
52  // Warning: this rule contains points on the boundary of the reference
53  // element, and therefore may be unsuitable for some problems. The alternative
54  // would be a 2x2x2 Gauss product rule.
55  const Real data[1][4] =
56  {
57  {1.0L, 0.0L, 0.0L, Real(4)/3}
58  };
59 
60  const unsigned int rule_id[1] = {
61  1 // (x,0,0) -> 6 permutations
62  };
63 
64  _points.resize(6);
65  _weights.resize(6);
66 
67  kim_rule(data, rule_id, 1);
68  return;
69  } // end case SECOND,THIRD
70 
71  case FOURTH:
72  case FIFTH:
73  {
74  // A degree 5, 13-point rule by Stroud,
75  // AH Stroud, "Some Fifth Degree Integration Formulas for Symmetric Regions II.",
76  // Numerische Mathematik 9, pp. 460-468 (1967).
77  //
78  // This rule is provably minimal in the number of points. The equations given for
79  // the n-cube on pg. 466 of the paper for mu/gamma and gamma are wrong, at least for
80  // the n=3 case. The analytical values given here were computed by me [JWP] in Maple.
81 
82  // Convenient intermediate values.
83  const Real sqrt19 = Real(std::sqrt(19.L));
84  const Real tp = Real(std::sqrt(71440 + 6802*sqrt19));
85 
86  // Point data for permutations.
87  const Real eta = 0;
88 
89  const Real lambda = Real(std::sqrt(1919.L/3285.L - 148.L*sqrt19/3285.L + 4.L*tp/3285.L));
90  // 8.8030440669930978047737818209860e-01L;
91 
92  const Real xi = Real(-std::sqrt(1121.L/3285.L + 74.L*sqrt19/3285.L - 2.L*tp/3285.L));
93  // -4.9584817142571115281421242364290e-01L;
94 
95  const Real mu = Real(std::sqrt(1121.L/3285.L + 74.L*sqrt19/3285.L + 2.L*tp/3285.L));
96  // 7.9562142216409541542982482567580e-01L;
97 
98  const Real gamma = Real(std::sqrt(1919.L/3285.L - 148.L*sqrt19/3285.L - 4.L*tp/3285.L));
99  // 2.5293711744842581347389255929324e-02L;
100 
101  // Weights: the centroid weight is given analytically. Weight B (resp C) goes
102  // with the {lambda,xi} (resp {gamma,mu}) permutation. The single-precision
103  // results reported by Stroud are given for reference.
104 
105  const Real A = Real(32)/19;
106  // Stroud: 0.21052632 * 8.0 = 1.684210560;
107 
108  const Real B = Real(1) / (Real(260072)/133225 - 1520*sqrt19/133225 + (133 - 37*sqrt19)*tp/133225);
109  // 5.4498735127757671684690782180890e-01L; // Stroud: 0.068123420 * 8.0 = 0.544987360;
110 
111  const Real C = Real(1) / (Real(260072)/133225 - 1520*sqrt19/133225 - (133 - 37*sqrt19)*tp/133225);
112  // 5.0764422766979170420572375713840e-01L; // Stroud: 0.063455527 * 8.0 = 0.507644216;
113 
114  _points.resize(13);
115  _weights.resize(13);
116 
117  unsigned int c=0;
118 
119  // Point with weight A (origin)
120  _points[c] = Point(eta, eta, eta);
121  _weights[c++] = A;
122 
123  // Points with weight B
124  _points[c] = Point(lambda, xi, xi);
125  _weights[c++] = B;
126  _points[c] = -_points[c-1];
127  _weights[c++] = B;
128 
129  _points[c] = Point(xi, lambda, xi);
130  _weights[c++] = B;
131  _points[c] = -_points[c-1];
132  _weights[c++] = B;
133 
134  _points[c] = Point(xi, xi, lambda);
135  _weights[c++] = B;
136  _points[c] = -_points[c-1];
137  _weights[c++] = B;
138 
139  // Points with weight C
140  _points[c] = Point(mu, mu, gamma);
141  _weights[c++] = C;
142  _points[c] = -_points[c-1];
143  _weights[c++] = C;
144 
145  _points[c] = Point(mu, gamma, mu);
146  _weights[c++] = C;
147  _points[c] = -_points[c-1];
148  _weights[c++] = C;
149 
150  _points[c] = Point(gamma, mu, mu);
151  _weights[c++] = C;
152  _points[c] = -_points[c-1];
153  _weights[c++] = C;
154 
155  return;
156 
157 
158  // // A degree 5, 14-point, "rotationally-symmetric" rule by
159  // // Kim and Song, Comm. Korean Math. Soc vol. 13, no. 4, 1998, pp. 913-931.
160  // // Was also reported in Stroud's 1971 book.
161  // const Real data[2][4] =
162  // {
163  // {7.95822425754221463264548820476135e-01L, 0.00000000000000000000000000000000e+00L, 0.00000000000000000000000000000000e+00L, 8.86426592797783933518005540166204e-01L},
164  // {7.58786910639328146269034278112267e-01L, 7.58786910639328146269034278112267e-01L, 7.58786910639328146269034278112267e-01L, 3.35180055401662049861495844875346e-01L}
165  // };
166 
167  // const unsigned int rule_id[2] = {
168  // 1, // (x,0,0) -> 6 permutations
169  // 4 // (x,x,x) -> 8 permutations
170  // };
171 
172  // _points.resize(14);
173  // _weights.resize(14);
174 
175  // kim_rule(data, rule_id, 2);
176  // return;
177  } // end case FOURTH,FIFTH
178 
179 
180  case SIXTH:
181  case SEVENTH:
182  {
183  if (allow_rules_with_negative_weights)
184  {
185  // A degree 7, 31-point, "rotationally-symmetric" rule by
186  // Kim and Song, Comm. Korean Math. Soc vol. 13, no. 4, 1998, pp. 913-931.
187  // This rule contains a negative weight, so only use it if such type of
188  // rules are allowed.
189  const Real data[3][4] =
190  {
191  {Real(0.00000000000000000000000000000000e+00L), Real(0.00000000000000000000000000000000e+00L), Real(0.00000000000000000000000000000000e+00L), Real(-1.27536231884057971014492753623188e+00L)},
192  {Real(5.85540043769119907612630781744060e-01L), Real(0.00000000000000000000000000000000e+00L), Real(0.00000000000000000000000000000000e+00L), Real(8.71111111111111111111111111111111e-01L)},
193  {Real(6.94470135991704766602025803883310e-01L), Real(9.37161638568208038511047377665396e-01L), Real(4.15659267604065126239606672567031e-01L), Real(1.68695652173913043478260869565217e-01L)}
194  };
195 
196  const unsigned int rule_id[3] = {
197  0, // (0,0,0) -> 1 permutation
198  1, // (x,0,0) -> 6 permutations
199  6 // (x,y,z) -> 24 permutations
200  };
201 
202  _points.resize(31);
203  _weights.resize(31);
204 
205  kim_rule(data, rule_id, 3);
206  return;
207  } // end if (allow_rules_with_negative_weights)
208 
209 
210  // A degree 7, 34-point, "fully-symmetric" rule, first published in
211  // P.C. Hammer and A.H. Stroud, "Numerical Evaluation of Multiple Integrals II",
212  // Mathematical Tables and Other Aids to Computation, vol 12., no 64, 1958, pp. 272-280
213  //
214  // This rule happens to fall under the same general
215  // construction as the Kim rules, so we've re-used
216  // that code here. Stroud gives 16 digits for his rule,
217  // and this is the most accurate version I've found.
218  //
219  // For comparison, a SEVENTH-order Gauss product rule
220  // (which integrates tri-7th order polynomials) would
221  // have 4^3=64 points.
222  const Real
223  r = Real(std::sqrt(6.L/7.L)),
224  s = Real(std::sqrt((960.L - 3.L*std::sqrt(28798.L)) / 2726.L)),
225  t = Real(std::sqrt((960.L + 3.L*std::sqrt(28798.L)) / 2726.L)),
226  B1 = Real(8624)/29160,
227  B2 = Real(2744)/29160,
228  B3 = 8*(774*t*t - 230)/(9720*(t*t-s*s)),
229  B4 = 8*(230 - 774*s*s)/(9720*(t*t-s*s));
230 
231  const Real data[4][4] =
232  {
233  {r, 0, 0, B1},
234  {r, r, 0, B2},
235  {s, s, s, B3},
236  {t, t, t, B4}
237  };
238 
239  const unsigned int rule_id[4] = {
240  1, // (x,0,0) -> 6 permutations
241  2, // (x,x,0) -> 12 permutations
242  4, // (x,x,x) -> 8 permutations
243  4 // (x,x,x) -> 8 permutations
244  };
245 
246  _points.resize(34);
247  _weights.resize(34);
248 
249  kim_rule(data, rule_id, 4);
250  return;
251 
252 
253  // // A degree 7, 38-point, "rotationally-symmetric" rule by
254  // // Kim and Song, Comm. Korean Math. Soc vol. 13, no. 4, 1998, pp. 913-931.
255  // //
256  // // This rule is obviously inferior to the 34-point rule above...
257  // const Real data[3][4] =
258  //{
259  // {9.01687807821291289082811566285950e-01L, 0.00000000000000000000000000000000e+00L, 0.00000000000000000000000000000000e+00L, 2.95189738262622903181631100062774e-01L},
260  // {4.08372221499474674069588900002128e-01L, 4.08372221499474674069588900002128e-01L, 4.08372221499474674069588900002128e-01L, 4.04055417266200582425904380777126e-01L},
261  // {8.59523090201054193116477875786220e-01L, 8.59523090201054193116477875786220e-01L, 4.14735913727987720499709244748633e-01L, 1.24850759678944080062624098058597e-01L}
262  //};
263  //
264  // const unsigned int rule_id[3] = {
265  //1, // (x,0,0) -> 6 permutations
266  //4, // (x,x,x) -> 8 permutations
267  //5 // (x,x,z) -> 24 permutations
268  // };
269  //
270  // _points.resize(38);
271  // _weights.resize(38);
272  //
273  // kim_rule(data, rule_id, 3);
274  // return;
275  } // end case SIXTH,SEVENTH
276 
277  case EIGHTH:
278  {
279  // A degree 8, 47-point, "rotationally-symmetric" rule by
280  // Kim and Song, Comm. Korean Math. Soc vol. 13, no. 4, 1998, pp. 913-931.
281  //
282  // A EIGHTH-order Gauss product rule (which integrates tri-8th order polynomials)
283  // would have 5^3=125 points.
284  const Real data[5][4] =
285  {
286  {Real(0.00000000000000000000000000000000e+00L), Real(0.00000000000000000000000000000000e+00L), Real(0.00000000000000000000000000000000e+00L), Real(4.51903714875199690490763818699555e-01L)},
287  {Real(7.82460796435951590652813975429717e-01L), Real(0.00000000000000000000000000000000e+00L), Real(0.00000000000000000000000000000000e+00L), Real(2.99379177352338919703385618576171e-01L)},
288  {Real(4.88094669706366480526729301468686e-01L), Real(4.88094669706366480526729301468686e-01L), Real(4.88094669706366480526729301468686e-01L), Real(3.00876159371240019939698689791164e-01L)},
289  {Real(8.62218927661481188856422891110042e-01L), Real(8.62218927661481188856422891110042e-01L), Real(8.62218927661481188856422891110042e-01L), Real(4.94843255877038125738173175714853e-02L)},
290  {Real(2.81113909408341856058098281846420e-01L), Real(9.44196578292008195318687494773744e-01L), Real(6.97574833707236996779391729948984e-01L), Real(1.22872389222467338799199767122592e-01L)}
291  };
292 
293  const unsigned int rule_id[5] = {
294  0, // (0,0,0) -> 1 permutation
295  1, // (x,0,0) -> 6 permutations
296  4, // (x,x,x) -> 8 permutations
297  4, // (x,x,x) -> 8 permutations
298  6 // (x,y,z) -> 24 permutations
299  };
300 
301  _points.resize(47);
302  _weights.resize(47);
303 
304  kim_rule(data, rule_id, 5);
305  return;
306  } // end case EIGHTH
307 
308 
309  // By default: construct and use a Gauss quadrature rule
310  default:
311  {
312  // Break out and fall down into the default: case for the
313  // outer switch statement.
314  break;
315  }
316 
317  } // end switch(_order + 2*p)
318  } // end case HEX8/20/27
319 
320  libmesh_fallthrough();
321 
322  // By default: construct and use a Gauss quadrature rule
323  default:
324  {
325  QGauss gauss_rule(3, _order);
326  gauss_rule.init(type_in, p);
327 
328  // Swap points and weights with the about-to-be destroyed rule.
329  _points.swap (gauss_rule.get_points() );
330  _weights.swap(gauss_rule.get_weights());
331 
332  return;
333  }
334  } // end switch (type_in)
335 }
libMesh::QBase::allow_rules_with_negative_weights
bool allow_rules_with_negative_weights
Definition: quadrature.h:246
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355
libMesh::QMonomial::kim_rule
void kim_rule(const Real rule_data[][4], const unsigned int *rule_id, const unsigned int n_pts)
Definition: quadrature_monomial.C:205
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
A
static PetscErrorCode Mat * A
Definition: petscdmlibmeshimpl.C:1020
data
IterBase * data
Definition: variant_filter_iterator.h:337

◆ kim_rule()

void libMesh::QMonomial::kim_rule ( const Real  rule_data[][4],
const unsigned int *  rule_id,
const unsigned int  n_pts 
)
private

Rules from Kim and Song, Comm. Korean Math. Soc vol. 13, no. 4, 1998, pp. 913-931. The rules are obtained by considering the group G^{rot} of rotations of the reference hex, and the invariant polynomials of this group.

In Kim and Song's rules, quadrature points are described by the following points and their unique permutations under the G^{rot} group:

0.) (0,0,0) ( 1 perm ) -> [0, 0, 0] 1.) (x,0,0) ( 6 perms) -> [x, 0, 0], [0, -x, 0], [-x, 0, 0], [0, x, 0], [0, 0, -x], [0, 0, x] 2.) (x,x,0) (12 perms) -> [x, x, 0], [x, -x, 0], [-x, -x, 0], [-x, x, 0], [x, 0, -x], [x, 0, x], [0, x, -x], [0, x, x], [0, -x, -x], [-x, 0, -x], [0, -x, x], [-x, 0, x] 3.) (x,y,0) (24 perms) -> [x, y, 0], [y, -x, 0], [-x, -y, 0], [-y, x, 0], [x, 0, -y], [x, -y, 0], [x, 0, y], [0, y, -x], [-x, y, 0], [0, y, x], [y, 0, -x], [0, -y, -x], [-y, 0, -x], [y, x, 0], [-y, -x, 0], [y, 0, x], [0, -y, x], [-y, 0, x], [-x, 0, y], [0, -x, -y], [0, -x, y], [-x, 0, -y], [0, x, y], [0, x, -y] 4.) (x,x,x) ( 8 perms) -> [x, x, x], [x, -x, x], [-x, -x, x], [-x, x, x], [x, x, -x], [x, -x, -x], [-x, x, -x], [-x, -x, -x] 5.) (x,x,z) (24 perms) -> [x, x, z], [x, -x, z], [-x, -x, z], [-x, x, z], [x, z, -x], [x, -x, -z], [x, -z, x], [z, x, -x], [-x, x, -z], [-z, x, x], [x, -z, -x], [-z, -x, -x], [-x, z, -x], [x, x, -z], [-x, -x, -z], [x, z, x], [z, -x, x], [-x, -z, x], [-x, z, x], [z, -x, -x], [-z, -x, x], [-x, -z, -x], [z, x, x], [-z, x, -x] 6.) (x,y,z) (24 perms) -> [x, y, z], [y, -x, z], [-x, -y, z], [-y, x, z], [x, z, -y], [x, -y, -z], [x, -z, y], [z, y, -x], [-x, y, -z], [-z, y, x], [y, -z, -x], [-z, -y, -x], [-y, z, -x], [y, x, -z], [-y, -x, -z], [y, z, x], [z, -y, x], [-y, -z, x], [-x, z, y], [z, -x, -y], [-z, -x, y], [-x, -z, -y], [z, x, y], [-z, x, -y]

Only two of Kim and Song's rules are particularly useful for FEM calculations: the degree 7, 38-point rule and their degree 8, 47-point rule. The others either contain negative weights or points outside the reference interval. The points and weights, to 32 digits, were obtained from: Ronald Cools' website (http://www.cs.kuleuven.ac.be/~nines/research/ecf/ecf.html) and the unique permutations of G^{rot} were computed by me [JWP] using Maple.

Definition at line 205 of file quadrature_monomial.C.

References libMesh::QBase::_points, libMesh::QBase::_weights, and libMesh::Real.

Referenced by init_3D().

208 {
209  for (unsigned int i=0, c=0; i<n_pts; ++i)
210  {
211  const Real
212  x=rule_data[i][0],
213  y=rule_data[i][1],
214  z=rule_data[i][2],
215  wt=rule_data[i][3];
216 
217  switch(rule_id[i])
218  {
219  case 0: // (0,0,0) 1 permutation
220  {
221  _points[c] = Point( x, y, z); _weights[c++] = wt;
222 
223  break;
224  }
225  case 1: // (x,0,0) 6 permutations
226  {
227  _points[c] = Point( x, 0., 0.); _weights[c++] = wt;
228  _points[c] = Point(0., -x, 0.); _weights[c++] = wt;
229  _points[c] = Point(-x, 0., 0.); _weights[c++] = wt;
230  _points[c] = Point(0., x, 0.); _weights[c++] = wt;
231  _points[c] = Point(0., 0., -x); _weights[c++] = wt;
232  _points[c] = Point(0., 0., x); _weights[c++] = wt;
233 
234  break;
235  }
236  case 2: // (x,x,0) 12 permutations
237  {
238  _points[c] = Point( x, x, 0.); _weights[c++] = wt;
239  _points[c] = Point( x, -x, 0.); _weights[c++] = wt;
240  _points[c] = Point(-x, -x, 0.); _weights[c++] = wt;
241  _points[c] = Point(-x, x, 0.); _weights[c++] = wt;
242  _points[c] = Point( x, 0., -x); _weights[c++] = wt;
243  _points[c] = Point( x, 0., x); _weights[c++] = wt;
244  _points[c] = Point(0., x, -x); _weights[c++] = wt;
245  _points[c] = Point(0., x, x); _weights[c++] = wt;
246  _points[c] = Point(0., -x, -x); _weights[c++] = wt;
247  _points[c] = Point(-x, 0., -x); _weights[c++] = wt;
248  _points[c] = Point(0., -x, x); _weights[c++] = wt;
249  _points[c] = Point(-x, 0., x); _weights[c++] = wt;
250 
251  break;
252  }
253  case 3: // (x,y,0) 24 permutations
254  {
255  _points[c] = Point( x, y, 0.); _weights[c++] = wt;
256  _points[c] = Point( y, -x, 0.); _weights[c++] = wt;
257  _points[c] = Point(-x, -y, 0.); _weights[c++] = wt;
258  _points[c] = Point(-y, x, 0.); _weights[c++] = wt;
259  _points[c] = Point( x, 0., -y); _weights[c++] = wt;
260  _points[c] = Point( x, -y, 0.); _weights[c++] = wt;
261  _points[c] = Point( x, 0., y); _weights[c++] = wt;
262  _points[c] = Point(0., y, -x); _weights[c++] = wt;
263  _points[c] = Point(-x, y, 0.); _weights[c++] = wt;
264  _points[c] = Point(0., y, x); _weights[c++] = wt;
265  _points[c] = Point( y, 0., -x); _weights[c++] = wt;
266  _points[c] = Point(0., -y, -x); _weights[c++] = wt;
267  _points[c] = Point(-y, 0., -x); _weights[c++] = wt;
268  _points[c] = Point( y, x, 0.); _weights[c++] = wt;
269  _points[c] = Point(-y, -x, 0.); _weights[c++] = wt;
270  _points[c] = Point( y, 0., x); _weights[c++] = wt;
271  _points[c] = Point(0., -y, x); _weights[c++] = wt;
272  _points[c] = Point(-y, 0., x); _weights[c++] = wt;
273  _points[c] = Point(-x, 0., y); _weights[c++] = wt;
274  _points[c] = Point(0., -x, -y); _weights[c++] = wt;
275  _points[c] = Point(0., -x, y); _weights[c++] = wt;
276  _points[c] = Point(-x, 0., -y); _weights[c++] = wt;
277  _points[c] = Point(0., x, y); _weights[c++] = wt;
278  _points[c] = Point(0., x, -y); _weights[c++] = wt;
279 
280  break;
281  }
282  case 4: // (x,x,x) 8 permutations
283  {
284  _points[c] = Point( x, x, x); _weights[c++] = wt;
285  _points[c] = Point( x, -x, x); _weights[c++] = wt;
286  _points[c] = Point(-x, -x, x); _weights[c++] = wt;
287  _points[c] = Point(-x, x, x); _weights[c++] = wt;
288  _points[c] = Point( x, x, -x); _weights[c++] = wt;
289  _points[c] = Point( x, -x, -x); _weights[c++] = wt;
290  _points[c] = Point(-x, x, -x); _weights[c++] = wt;
291  _points[c] = Point(-x, -x, -x); _weights[c++] = wt;
292 
293  break;
294  }
295  case 5: // (x,x,z) 24 permutations
296  {
297  _points[c] = Point( x, x, z); _weights[c++] = wt;
298  _points[c] = Point( x, -x, z); _weights[c++] = wt;
299  _points[c] = Point(-x, -x, z); _weights[c++] = wt;
300  _points[c] = Point(-x, x, z); _weights[c++] = wt;
301  _points[c] = Point( x, z, -x); _weights[c++] = wt;
302  _points[c] = Point( x, -x, -z); _weights[c++] = wt;
303  _points[c] = Point( x, -z, x); _weights[c++] = wt;
304  _points[c] = Point( z, x, -x); _weights[c++] = wt;
305  _points[c] = Point(-x, x, -z); _weights[c++] = wt;
306  _points[c] = Point(-z, x, x); _weights[c++] = wt;
307  _points[c] = Point( x, -z, -x); _weights[c++] = wt;
308  _points[c] = Point(-z, -x, -x); _weights[c++] = wt;
309  _points[c] = Point(-x, z, -x); _weights[c++] = wt;
310  _points[c] = Point( x, x, -z); _weights[c++] = wt;
311  _points[c] = Point(-x, -x, -z); _weights[c++] = wt;
312  _points[c] = Point( x, z, x); _weights[c++] = wt;
313  _points[c] = Point( z, -x, x); _weights[c++] = wt;
314  _points[c] = Point(-x, -z, x); _weights[c++] = wt;
315  _points[c] = Point(-x, z, x); _weights[c++] = wt;
316  _points[c] = Point( z, -x, -x); _weights[c++] = wt;
317  _points[c] = Point(-z, -x, x); _weights[c++] = wt;
318  _points[c] = Point(-x, -z, -x); _weights[c++] = wt;
319  _points[c] = Point( z, x, x); _weights[c++] = wt;
320  _points[c] = Point(-z, x, -x); _weights[c++] = wt;
321 
322  break;
323  }
324  case 6: // (x,y,z) 24 permutations
325  {
326  _points[c] = Point( x, y, z); _weights[c++] = wt;
327  _points[c] = Point( y, -x, z); _weights[c++] = wt;
328  _points[c] = Point(-x, -y, z); _weights[c++] = wt;
329  _points[c] = Point(-y, x, z); _weights[c++] = wt;
330  _points[c] = Point( x, z, -y); _weights[c++] = wt;
331  _points[c] = Point( x, -y, -z); _weights[c++] = wt;
332  _points[c] = Point( x, -z, y); _weights[c++] = wt;
333  _points[c] = Point( z, y, -x); _weights[c++] = wt;
334  _points[c] = Point(-x, y, -z); _weights[c++] = wt;
335  _points[c] = Point(-z, y, x); _weights[c++] = wt;
336  _points[c] = Point( y, -z, -x); _weights[c++] = wt;
337  _points[c] = Point(-z, -y, -x); _weights[c++] = wt;
338  _points[c] = Point(-y, z, -x); _weights[c++] = wt;
339  _points[c] = Point( y, x, -z); _weights[c++] = wt;
340  _points[c] = Point(-y, -x, -z); _weights[c++] = wt;
341  _points[c] = Point( y, z, x); _weights[c++] = wt;
342  _points[c] = Point( z, -y, x); _weights[c++] = wt;
343  _points[c] = Point(-y, -z, x); _weights[c++] = wt;
344  _points[c] = Point(-x, z, y); _weights[c++] = wt;
345  _points[c] = Point( z, -x, -y); _weights[c++] = wt;
346  _points[c] = Point(-z, -x, y); _weights[c++] = wt;
347  _points[c] = Point(-x, -z, -y); _weights[c++] = wt;
348  _points[c] = Point( z, x, y); _weights[c++] = wt;
349  _points[c] = Point(-z, x, -y); _weights[c++] = wt;
350 
351  break;
352  }
353  default:
354  libmesh_error_msg("Unknown rule ID: " << rule_id[i] << "!");
355  } // end switch(rule_id[i])
356  }
357 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131

◆ n_objects()

static unsigned int libMesh::ReferenceCounter::n_objects ( )
inlinestaticinherited

Prints the number of outstanding (created, but not yet destroyed) objects.

Definition at line 83 of file reference_counter.h.

References libMesh::ReferenceCounter::_n_objects.

84  { return _n_objects; }
libMesh::ReferenceCounter::_n_objects
static Threads::atomic< unsigned int > _n_objects
Definition: reference_counter.h:130

◆ n_points()

unsigned int libMesh::QBase::n_points ( ) const
inlineinherited
Returns
The number of points associated with the quadrature rule.

Definition at line 127 of file quadrature.h.

References libMesh::QBase::_points.

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::System::calculate_norm(), libMesh::FirstOrderUnsteadySolver::compute_second_order_eqns(), libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), libMesh::QConical::conical_product_tri(), libMesh::QBase::print_info(), libMesh::QBase::tensor_product_hex(), libMesh::QBase::tensor_product_prism(), and libMesh::QBase::tensor_product_quad().

128  {
129  libmesh_assert (!_points.empty());
130  return cast_int<unsigned int>(_points.size());
131  }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349

◆ operator=() [1/2]

QMonomial& libMesh::QMonomial::operator= ( const QMonomial &  )
default

◆ operator=() [2/2]

QMonomial& libMesh::QMonomial::operator= ( QMonomial &&  )
default

◆ print_info() [1/2]

void libMesh::ReferenceCounter::print_info ( std::ostream &  out = libMesh::out)
staticinherited

Prints the reference information, by default to libMesh::out.

Definition at line 87 of file reference_counter.C.

References libMesh::ReferenceCounter::_enable_print_counter, and libMesh::ReferenceCounter::get_info().

88 {
89  if (_enable_print_counter)
90  out_stream << ReferenceCounter::get_info();
91 }
libMesh::ReferenceCounter::get_info
static std::string get_info()
Definition: reference_counter.C:47

◆ print_info() [2/2]

void libMesh::QBase::print_info ( std::ostream &  os = libMesh::out) const
inlineinherited

Prints information relevant to the quadrature rule, by default to libMesh::out.

Definition at line 378 of file quadrature.h.

References libMesh::QBase::_points, libMesh::QBase::_weights, libMesh::QBase::n_points(), and libMesh::Real.

Referenced by libMesh::operator<<().

379 {
380  libmesh_assert(!_points.empty());
381  libmesh_assert(!_weights.empty());
382 
383  Real summed_weights=0;
384  os << "N_Q_Points=" << this->n_points() << std::endl << std::endl;
385  for (unsigned int qpoint=0; qpoint<this->n_points(); qpoint++)
386  {
387  os << " Point " << qpoint << ":\n"
388  << " "
389  << _points[qpoint]
390  << "\n Weight:\n "
391  << " w=" << _weights[qpoint] << "\n" << std::endl;
392 
393  summed_weights += _weights[qpoint];
394  }
395  os << "Summed Weights: " << summed_weights << std::endl;
396 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355
libMesh::QBase::n_points
unsigned int n_points() const
Definition: quadrature.h:127
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131

◆ qp()

Point libMesh::QBase::qp ( const unsigned int  i) const
inlineinherited
Returns
The 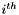$ i^{th} $ quadrature point in reference element space.

Definition at line 165 of file quadrature.h.

References libMesh::QBase::_points.

Referenced by libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), libMesh::QConical::conical_product_tri(), libMesh::QBase::tensor_product_hex(), libMesh::QBase::tensor_product_prism(), and libMesh::QBase::tensor_product_quad().

166  {
167  libmesh_assert_less (i, _points.size());
168  return _points[i];
169  }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349

◆ scale()

void libMesh::QBase::scale ( std::pair< Real, Real >  old_range,
std::pair< Real, Real >  new_range 
)
inherited

Maps the points of a 1D quadrature rule defined by "old_range" to another 1D interval defined by "new_range" and scales the weights accordingly.

Definition at line 93 of file quadrature.C.

References libMesh::QBase::_dim, libMesh::QBase::_points, libMesh::QBase::_weights, and libMesh::Real.

Referenced by libMesh::QConical::conical_product_tet(), and libMesh::QConical::conical_product_tri().

95 {
96  // Make sure we are in 1D
97  libmesh_assert_equal_to (_dim, 1);
98 
99  Real
100  h_new = new_range.second - new_range.first,
101  h_old = old_range.second - old_range.first;
102 
103  // Make sure that we have sane ranges
104  libmesh_assert_greater (h_new, 0.);
105  libmesh_assert_greater (h_old, 0.);
106 
107  // Make sure there are some points
108  libmesh_assert_greater (_points.size(), 0);
109 
110  // Compute the scale factor
111  Real scfact = h_new/h_old;
112 
113  // We're mapping from old_range -> new_range
114  for (std::size_t i=0; i<_points.size(); i++)
115  {
116  _points[i](0) = new_range.first +
117  (_points[i](0) - old_range.first) * scfact;
118 
119  // Scale the weights
120  _weights[i] *= scfact;
121  }
122 }
libMesh::QBase::_dim
unsigned int _dim
Definition: quadrature.h:325
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131

◆ shapes_need_reinit()

virtual bool libMesh::QBase::shapes_need_reinit ( )
inlinevirtualinherited
Returns
true if the shape functions need to be recalculated, false otherwise.

This may be required if the number of quadrature points or their position changes.

Definition at line 231 of file quadrature.h.

231 { return false; }

◆ stroud_rule()

void libMesh::QMonomial::stroud_rule ( const Real  rule_data[][3],
const unsigned int *  rule_symmetry,
const unsigned int  n_pts 
)
private

Stroud's rules for quads and hexes can have one of several different types of symmetry. The rule_symmetry array describes how the different lines of the rule_data array are to be applied. The different rule_symmetry possibilities are: 0) Origin or single-point: (x,y) Fully-symmetric, 3 cases: 1) (x,y) -> (x,y), (-x,y), (x,-y), (-x,-y) (y,x), (-y,x), (y,-x), (-y,-x) 2) (x,x) -> (x,x), (-x,x), (x,-x), (-x,-x) 3) (x,0) -> (x,0), (-x,0), (0, x), ( 0,-x) 4) Rotational Invariant, (x,y) -> (x,y), (-x,-y), (-y, x), (y,-x) 5) Partial Symmetry, (x,y) -> (x,y), (-x, y) [x!=0] 6) Rectangular Symmetry, (x,y) -> (x,y), (-x, y), (-x,-y), (x,-y) 7) Central Symmetry, (0,y) -> (0,y), ( 0,-y)

Not all rules with these symmetries are due to Stroud, however, his book is probably the most frequently-cited compendium of quadrature rules and later authors certainly built upon his work.

Definition at line 57 of file quadrature_monomial.C.

References libMesh::QBase::_points, libMesh::QBase::_weights, and libMesh::Real.

Referenced by init_2D().

60 {
61  for (unsigned int i=0, c=0; i<n_pts; ++i)
62  {
63  const Real
64  x=rule_data[i][0],
65  y=rule_data[i][1],
66  wt=rule_data[i][2];
67 
68  switch(rule_symmetry[i])
69  {
70  case 0: // Single point (no symmetry)
71  {
72  _points[c] = Point( x, y);
73  _weights[c++] = wt;
74 
75  break;
76  }
77  case 1: // Fully-symmetric (x,y)
78  {
79  _points[c] = Point( x, y);
80  _weights[c++] = wt;
81 
82  _points[c] = Point(-x, y);
83  _weights[c++] = wt;
84 
85  _points[c] = Point( x,-y);
86  _weights[c++] = wt;
87 
88  _points[c] = Point(-x,-y);
89  _weights[c++] = wt;
90 
91  _points[c] = Point( y, x);
92  _weights[c++] = wt;
93 
94  _points[c] = Point(-y, x);
95  _weights[c++] = wt;
96 
97  _points[c] = Point( y,-x);
98  _weights[c++] = wt;
99 
100  _points[c] = Point(-y,-x);
101  _weights[c++] = wt;
102 
103  break;
104  }
105  case 2: // Fully-symmetric (x,x)
106  {
107  _points[c] = Point( x, x);
108  _weights[c++] = wt;
109 
110  _points[c] = Point(-x, x);
111  _weights[c++] = wt;
112 
113  _points[c] = Point( x,-x);
114  _weights[c++] = wt;
115 
116  _points[c] = Point(-x,-x);
117  _weights[c++] = wt;
118 
119  break;
120  }
121  case 3: // Fully-symmetric (x,0)
122  {
123  libmesh_assert_equal_to (y, 0.0);
124 
125  _points[c] = Point( x,0.);
126  _weights[c++] = wt;
127 
128  _points[c] = Point(-x,0.);
129  _weights[c++] = wt;
130 
131  _points[c] = Point(0., x);
132  _weights[c++] = wt;
133 
134  _points[c] = Point(0.,-x);
135  _weights[c++] = wt;
136 
137  break;
138  }
139  case 4: // Rotational invariant
140  {
141  _points[c] = Point( x, y);
142  _weights[c++] = wt;
143 
144  _points[c] = Point(-x,-y);
145  _weights[c++] = wt;
146 
147  _points[c] = Point(-y, x);
148  _weights[c++] = wt;
149 
150  _points[c] = Point( y,-x);
151  _weights[c++] = wt;
152 
153  break;
154  }
155  case 5: // Partial symmetry (Wissman's rules)
156  {
157  libmesh_assert_not_equal_to (x, 0.0);
158 
159  _points[c] = Point( x, y);
160  _weights[c++] = wt;
161 
162  _points[c] = Point(-x, y);
163  _weights[c++] = wt;
164 
165  break;
166  }
167  case 6: // Rectangular symmetry
168  {
169  _points[c] = Point( x, y);
170  _weights[c++] = wt;
171 
172  _points[c] = Point(-x, y);
173  _weights[c++] = wt;
174 
175  _points[c] = Point(-x,-y);
176  _weights[c++] = wt;
177 
178  _points[c] = Point( x,-y);
179  _weights[c++] = wt;
180 
181  break;
182  }
183  case 7: // Central symmetry
184  {
185  libmesh_assert_equal_to (x, 0.0);
186  libmesh_assert_not_equal_to (y, 0.0);
187 
188  _points[c] = Point(0., y);
189  _weights[c++] = wt;
190 
191  _points[c] = Point(0.,-y);
192  _weights[c++] = wt;
193 
194  break;
195  }
196  default:
197  libmesh_error_msg("Unknown symmetry!");
198  } // end switch(rule_symmetry[i])
199  }
200 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131

◆ tensor_product_hex()

void libMesh::QBase::tensor_product_hex ( const QBase &  q1D)
protectedinherited

Computes the tensor product quadrature rule [q1D x q1D x q1D] from the 1D rule q1D. Used in the init_3D routines for hexahedral element types.

Definition at line 154 of file quadrature.C.

References libMesh::QBase::_points, libMesh::QBase::_weights, libMesh::QBase::n_points(), libMesh::QBase::qp(), and libMesh::QBase::w().

Referenced by libMesh::QGaussLobatto::init_3D(), libMesh::QTrap::init_3D(), libMesh::QGrid::init_3D(), libMesh::QSimpson::init_3D(), and libMesh::QGauss::init_3D().

155 {
156  const unsigned int np = q1D.n_points();
157 
158  _points.resize(np * np * np);
159 
160  _weights.resize(np * np * np);
161 
162  unsigned int q=0;
163 
164  for (unsigned int k=0; k<np; k++)
165  for (unsigned int j=0; j<np; j++)
166  for (unsigned int i=0; i<np; i++)
167  {
168  _points[q](0) = q1D.qp(i)(0);
169  _points[q](1) = q1D.qp(j)(0);
170  _points[q](2) = q1D.qp(k)(0);
171 
172  _weights[q] = q1D.w(i) * q1D.w(j) * q1D.w(k);
173 
174  q++;
175  }
176 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ tensor_product_prism()

void libMesh::QBase::tensor_product_prism ( const QBase &  q1D,
const QBase &  q2D 
)
protectedinherited

Computes the tensor product of a 1D quadrature rule and a 2D quadrature rule. Used in the init_3D routines for prismatic element types.

Definition at line 181 of file quadrature.C.

References libMesh::QBase::_points, libMesh::QBase::_weights, libMesh::QBase::n_points(), libMesh::QBase::qp(), and libMesh::QBase::w().

Referenced by libMesh::QGrid::init_3D(), libMesh::QTrap::init_3D(), libMesh::QSimpson::init_3D(), and libMesh::QGauss::init_3D().

182 {
183  const unsigned int n_points1D = q1D.n_points();
184  const unsigned int n_points2D = q2D.n_points();
185 
186  _points.resize (n_points1D * n_points2D);
187  _weights.resize (n_points1D * n_points2D);
188 
189  unsigned int q=0;
190 
191  for (unsigned int j=0; j<n_points1D; j++)
192  for (unsigned int i=0; i<n_points2D; i++)
193  {
194  _points[q](0) = q2D.qp(i)(0);
195  _points[q](1) = q2D.qp(i)(1);
196  _points[q](2) = q1D.qp(j)(0);
197 
198  _weights[q] = q2D.w(i) * q1D.w(j);
199 
200  q++;
201  }
202 
203 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ tensor_product_quad()

void libMesh::QBase::tensor_product_quad ( const QBase &  q1D)
protectedinherited

Constructs a 2D rule from the tensor product of q1D with itself. Used in the init_2D() routines for quadrilateral element types.

Definition at line 127 of file quadrature.C.

References libMesh::QBase::_points, libMesh::QBase::_weights, libMesh::QBase::n_points(), libMesh::QBase::qp(), and libMesh::QBase::w().

Referenced by libMesh::QGaussLobatto::init_2D(), libMesh::QTrap::init_2D(), libMesh::QGrid::init_2D(), libMesh::QSimpson::init_2D(), and libMesh::QGauss::init_2D().

128 {
129 
130  const unsigned int np = q1D.n_points();
131 
132  _points.resize(np * np);
133 
134  _weights.resize(np * np);
135 
136  unsigned int q=0;
137 
138  for (unsigned int j=0; j<np; j++)
139  for (unsigned int i=0; i<np; i++)
140  {
141  _points[q](0) = q1D.qp(i)(0);
142  _points[q](1) = q1D.qp(j)(0);
143 
144  _weights[q] = q1D.w(i)*q1D.w(j);
145 
146  q++;
147  }
148 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ type()

QuadratureType libMesh::QMonomial::type ( ) const
overridevirtual
Returns
QMONOMIAL.

Implements libMesh::QBase.

Definition at line 32 of file quadrature_monomial.C.

References libMesh::QMONOMIAL.

33 {
34  return QMONOMIAL;
35 }

◆ w()

Real libMesh::QBase::w ( const unsigned int  i) const
inlineinherited
Returns
The 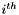$ i^{th} $ quadrature weight.

Definition at line 174 of file quadrature.h.

References libMesh::QBase::_weights.

Referenced by libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), libMesh::QConical::conical_product_tri(), libMesh::QBase::tensor_product_hex(), libMesh::QBase::tensor_product_prism(), and libMesh::QBase::tensor_product_quad().

175  {
176  libmesh_assert_less (i, _weights.size());
177  return _weights[i];
178  }
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

◆ wissmann_rule()

void libMesh::QMonomial::wissmann_rule ( const Real  rule_data[][3],
const unsigned int  n_pts 
)
private

Wissmann published three interesting "partially symmetric" rules for integrating degree 4, 6, and 8 polynomials exactly on QUADs. These rules have all positive weights, all points inside the reference element, and have fewer points than tensor-product rules of equivalent order, making them superior to those rules for monomial bases.

J. W. Wissman and T. Becker, Partially symmetric cubature formulas for even degrees of exactness, SIAM J. Numer. Anal. 23 (1986), 676–685.

Definition at line 37 of file quadrature_monomial.C.

References libMesh::QBase::_points, and libMesh::QBase::_weights.

Referenced by init_2D().

39 {
40  for (unsigned int i=0, c=0; i<n_pts; ++i)
41  {
42  _points[c] = Point( rule_data[i][0], rule_data[i][1] );
43  _weights[c++] = rule_data[i][2];
44 
45  // This may be an (x1,x2) -> (-x1,x2) point, in which case
46  // we will also generate the mirror point using the same weight.
47  if (rule_data[i][0] != static_cast<Real>(0.0))
48  {
49  _points[c] = Point( -rule_data[i][0], rule_data[i][1] );
50  _weights[c++] = rule_data[i][2];
51  }
52  }
53 }
libMesh::QBase::_points
std::vector< Point > _points
Definition: quadrature.h:349
libMesh::QBase::_weights
std::vector< Real > _weights
Definition: quadrature.h:355

Member Data Documentation

◆ _counts

ReferenceCounter::Counts libMesh::ReferenceCounter::_counts
staticprotectedinherited

Actually holds the data.

Definition at line 122 of file reference_counter.h.

Referenced by libMesh::ReferenceCounter::get_info(), libMesh::ReferenceCounter::increment_constructor_count(), and libMesh::ReferenceCounter::increment_destructor_count().

◆ _dim

unsigned int libMesh::QBase::_dim
protectedinherited

The spatial dimension of the quadrature rule.

Definition at line 325 of file quadrature.h.

Referenced by libMesh::QBase::build(), libMesh::QBase::get_dim(), libMesh::QBase::init(), libMesh::QGaussLobatto::QGaussLobatto(), libMesh::QJacobi::QJacobi(), libMesh::QSimpson::QSimpson(), libMesh::QTrap::QTrap(), and libMesh::QBase::scale().

◆ _enable_print_counter

bool libMesh::ReferenceCounter::_enable_print_counter = true
staticprotectedinherited

Flag to control whether reference count information is printed when print_info is called.

Definition at line 141 of file reference_counter.h.

Referenced by libMesh::ReferenceCounter::disable_print_counter_info(), libMesh::ReferenceCounter::enable_print_counter_info(), and libMesh::ReferenceCounter::print_info().

◆ _mutex

Threads::spin_mutex libMesh::ReferenceCounter::_mutex
staticprotectedinherited

Mutual exclusion object to enable thread-safe reference counting.

Definition at line 135 of file reference_counter.h.

◆ _n_objects

Threads::atomic< unsigned int > libMesh::ReferenceCounter::_n_objects
staticprotectedinherited

The number of objects. Print the reference count information when the number returns to 0.

Definition at line 130 of file reference_counter.h.

Referenced by libMesh::ReferenceCounter::n_objects(), libMesh::ReferenceCounter::ReferenceCounter(), and libMesh::ReferenceCounter::~ReferenceCounter().

◆ _order

Order libMesh::QBase::_order
protectedinherited

The polynomial order which the quadrature rule is capable of integrating exactly.

Definition at line 331 of file quadrature.h.

Referenced by libMesh::QBase::build(), libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), libMesh::QConical::conical_product_tri(), libMesh::QBase::get_order(), libMesh::QClough::init_1D(), libMesh::QGaussLobatto::init_1D(), libMesh::QConical::init_1D(), libMesh::QGrid::init_1D(), libMesh::QGauss::init_1D(), libMesh::QJacobi::init_1D(), init_1D(), libMesh::QGrundmann_Moller::init_1D(), libMesh::QClough::init_2D(), libMesh::QGaussLobatto::init_2D(), libMesh::QGrid::init_2D(), libMesh::QGauss::init_2D(), init_2D(), libMesh::QGrundmann_Moller::init_2D(), libMesh::QGaussLobatto::init_3D(), libMesh::QGrid::init_3D(), libMesh::QGauss::init_3D(), init_3D(), and libMesh::QGrundmann_Moller::init_3D().

◆ _p_level

unsigned int libMesh::QBase::_p_level
protectedinherited

The p-level of the element for which the current values have been computed.

Definition at line 343 of file quadrature.h.

Referenced by libMesh::QBase::get_order(), libMesh::QBase::get_p_level(), and libMesh::QBase::init().

◆ _points

std::vector<Point> libMesh::QBase::_points
protectedinherited

The locations of the quadrature points in reference element space.

Definition at line 349 of file quadrature.h.

Referenced by libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), libMesh::QConical::conical_product_tri(), libMesh::QGauss::dunavant_rule(), libMesh::QGauss::dunavant_rule2(), libMesh::QBase::get_points(), libMesh::QGrundmann_Moller::gm_rule(), libMesh::QBase::init_0D(), libMesh::QClough::init_1D(), libMesh::QGaussLobatto::init_1D(), libMesh::QConical::init_1D(), libMesh::QTrap::init_1D(), libMesh::QGrid::init_1D(), libMesh::QSimpson::init_1D(), libMesh::QGauss::init_1D(), libMesh::QJacobi::init_1D(), init_1D(), libMesh::QGrundmann_Moller::init_1D(), libMesh::QClough::init_2D(), libMesh::QTrap::init_2D(), libMesh::QGrid::init_2D(), libMesh::QSimpson::init_2D(), libMesh::QGauss::init_2D(), init_2D(), libMesh::QGrid::init_3D(), libMesh::QTrap::init_3D(), libMesh::QGauss::init_3D(), libMesh::QSimpson::init_3D(), init_3D(), libMesh::QGrundmann_Moller::init_3D(), libMesh::QGauss::keast_rule(), kim_rule(), libMesh::QBase::n_points(), libMesh::QBase::print_info(), libMesh::QBase::qp(), libMesh::QBase::scale(), stroud_rule(), libMesh::QBase::tensor_product_hex(), libMesh::QBase::tensor_product_prism(), libMesh::QBase::tensor_product_quad(), and wissmann_rule().

◆ _type

ElemType libMesh::QBase::_type
protectedinherited

The type of element for which the current values have been computed.

Definition at line 337 of file quadrature.h.

Referenced by libMesh::QBase::get_elem_type(), and libMesh::QBase::init().

◆ _weights

std::vector<Real> libMesh::QBase::_weights
protectedinherited

The quadrature weights. The order of the weights matches the ordering of the _points vector.

Definition at line 355 of file quadrature.h.

Referenced by libMesh::QConical::conical_product_pyramid(), libMesh::QConical::conical_product_tet(), libMesh::QConical::conical_product_tri(), libMesh::QGauss::dunavant_rule(), libMesh::QGauss::dunavant_rule2(), libMesh::QBase::get_weights(), libMesh::QGrundmann_Moller::gm_rule(), libMesh::QBase::init_0D(), libMesh::QClough::init_1D(), libMesh::QGaussLobatto::init_1D(), libMesh::QConical::init_1D(), libMesh::QTrap::init_1D(), libMesh::QGrid::init_1D(), libMesh::QSimpson::init_1D(), libMesh::QGauss::init_1D(), libMesh::QJacobi::init_1D(), init_1D(), libMesh::QGrundmann_Moller::init_1D(), libMesh::QClough::init_2D(), libMesh::QTrap::init_2D(), libMesh::QGrid::init_2D(), libMesh::QGauss::init_2D(), libMesh::QSimpson::init_2D(), init_2D(), libMesh::QGrid::init_3D(), libMesh::QTrap::init_3D(), libMesh::QSimpson::init_3D(), libMesh::QGauss::init_3D(), init_3D(), libMesh::QGrundmann_Moller::init_3D(), libMesh::QGauss::keast_rule(), kim_rule(), libMesh::QBase::print_info(), libMesh::QBase::scale(), stroud_rule(), libMesh::QBase::tensor_product_hex(), libMesh::QBase::tensor_product_prism(), libMesh::QBase::tensor_product_quad(), libMesh::QBase::w(), and wissmann_rule().

◆ allow_rules_with_negative_weights

bool libMesh::QBase::allow_rules_with_negative_weights
inherited

Flag (default true) controlling the use of quadrature rules with negative weights. Set this to false to require rules with all positive weights.

Rules with negative weights can be unsuitable for some problems. For example, it is possible for a rule with negative weights to obtain a negative result when integrating a positive function.

A particular example: if rules with negative weights are not allowed, a request for TET,THIRD (5 points) will return the TET,FIFTH (14 points) rule instead, nearly tripling the computational effort required!

Definition at line 246 of file quadrature.h.

Referenced by libMesh::QGrundmann_Moller::init_2D(), libMesh::QGauss::init_3D(), init_3D(), and libMesh::QGrundmann_Moller::init_3D().

The documentation for this class was generated from the following files:
generated by doxygen