Classes | Public Types | Public Member Functions | Static Public Member Functions | Protected Types | Protected Member Functions | Static Protected Member Functions | Protected Attributes | Static Protected Attributes | Private Member Functions | Static Private Attributes | Friends | List of all members
libMesh::InfFE< Dim, T_radial, T_map > Class Template Reference

Base class for all the infinite geometric element types. More...

#include <fe.h>

Inheritance diagram for libMesh::InfFE< Dim, T_radial, T_map >:
Inheritance graph
[legend]

Classes

class  Base
 
class  Radial
 

Public Types

typedef OutputType OutputShape
 
typedef TensorTools::IncrementRank< OutputShape >::type OutputGradient
 
typedef TensorTools::IncrementRank< OutputGradient >::type OutputTensor
 
typedef TensorTools::DecrementRank< OutputShape >::type OutputDivergence
 
typedef TensorTools::MakeNumber< OutputShape >::type OutputNumber
 
typedef TensorTools::IncrementRank< OutputNumber >::type OutputNumberGradient
 
typedef TensorTools::IncrementRank< OutputNumberGradient >::type OutputNumberTensor
 
typedef TensorTools::DecrementRank< OutputNumber >::type OutputNumberDivergence
 

Public Member Functions

 InfFE (const FEType &fet)
 
 ~InfFE ()
 
virtual FEContinuity get_continuity () const override
 
virtual bool is_hierarchic () const override
 
virtual void reinit (const Elem *elem, const std::vector< Point > *const pts=nullptr, const std::vector< Real > *const weights=nullptr) override
 
virtual void reinit (const Elem *elem, const unsigned int side, const Real tolerance=TOLERANCE, const std::vector< Point > *const pts=nullptr, const std::vector< Real > *const weights=nullptr) override
 
virtual void edge_reinit (const Elem *elem, const unsigned int edge, const Real tolerance=TOLERANCE, const std::vector< Point > *const pts=nullptr, const std::vector< Real > *const weights=nullptr) override
 
virtual void side_map (const Elem *, const Elem *, const unsigned int, const std::vector< Point > &, std::vector< Point > &) override
 
virtual void attach_quadrature_rule (QBase *q) override
 
virtual unsigned int n_shape_functions () const override
 
virtual unsigned int n_quadrature_points () const override
 
template<>
std::unique_ptr< FEGenericBase< Real > > build (const unsigned int dim, const FEType &fet)
 
template<>
std::unique_ptr< FEGenericBase< RealGradient > > build (const unsigned int dim, const FEType &fet)
 
template<>
std::unique_ptr< FEGenericBase< Real > > build_InfFE (const unsigned int dim, const FEType &fet)
 
template<>
std::unique_ptr< FEGenericBase< RealGradient > > build_InfFE (const unsigned int, const FEType &)
 
const std::vector< std::vector< OutputShape > > & get_phi () const
 
const std::vector< std::vector< OutputGradient > > & get_dphi () const
 
const std::vector< std::vector< OutputShape > > & get_curl_phi () const
 
const std::vector< std::vector< OutputDivergence > > & get_div_phi () const
 
const std::vector< std::vector< OutputShape > > & get_dphidx () const
 
const std::vector< std::vector< OutputShape > > & get_dphidy () const
 
const std::vector< std::vector< OutputShape > > & get_dphidz () const
 
const std::vector< std::vector< OutputShape > > & get_dphidxi () const
 
const std::vector< std::vector< OutputShape > > & get_dphideta () const
 
const std::vector< std::vector< OutputShape > > & get_dphidzeta () const
 
const std::vector< std::vector< OutputTensor > > & get_d2phi () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidx2 () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidxdy () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidxdz () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidy2 () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidydz () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidz2 () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidxi2 () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidxideta () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidxidzeta () const
 
const std::vector< std::vector< OutputShape > > & get_d2phideta2 () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidetadzeta () const
 
const std::vector< std::vector< OutputShape > > & get_d2phidzeta2 () const
 
const std::vector< OutputGradient > & get_dphase () const
 
const std::vector< Real > & get_Sobolev_weight () const
 
const std::vector< RealGradient > & get_Sobolev_dweight () const
 
void print_phi (std::ostream &os) const
 
void print_dphi (std::ostream &os) const
 
void print_d2phi (std::ostream &os) const
 
unsigned int get_dim () const
 
const std::vector< Point > & get_xyz () const
 
const std::vector< Real > & get_JxW () const
 
const std::vector< RealGradient > & get_dxyzdxi () const
 
const std::vector< RealGradient > & get_dxyzdeta () const
 
const std::vector< RealGradient > & get_dxyzdzeta () const
 
const std::vector< RealGradient > & get_d2xyzdxi2 () const
 
const std::vector< RealGradient > & get_d2xyzdeta2 () const
 
const std::vector< RealGradient > & get_d2xyzdzeta2 () const
 
const std::vector< RealGradient > & get_d2xyzdxideta () const
 
const std::vector< RealGradient > & get_d2xyzdxidzeta () const
 
const std::vector< RealGradient > & get_d2xyzdetadzeta () const
 
const std::vector< Real > & get_dxidx () const
 
const std::vector< Real > & get_dxidy () const
 
const std::vector< Real > & get_dxidz () const
 
const std::vector< Real > & get_detadx () const
 
const std::vector< Real > & get_detady () const
 
const std::vector< Real > & get_detadz () const
 
const std::vector< Real > & get_dzetadx () const
 
const std::vector< Real > & get_dzetady () const
 
const std::vector< Real > & get_dzetadz () const
 
const std::vector< std::vector< Point > > & get_tangents () const
 
const std::vector< Point > & get_normals () const
 
const std::vector< Real > & get_curvatures () const
 
ElemType get_type () const
 
unsigned int get_p_level () const
 
FEType get_fe_type () const
 
Order get_order () const
 
void set_fe_order (int new_order)
 
FEFamily get_family () const
 
const FEMap & get_fe_map () const
 
void print_JxW (std::ostream &os) const
 
void print_xyz (std::ostream &os) const
 
void print_info (std::ostream &os) const
 

Static Public Member Functions

static Real shape (const FEType &fet, const ElemType t, const unsigned int i, const Point &p)
 
static Real shape (const FEType &fet, const Elem *elem, const unsigned int i, const Point &p)
 
static void compute_data (const FEType &fe_t, const Elem *inf_elem, FEComputeData &data)
 
static unsigned int n_shape_functions (const FEType &fet, const ElemType t)
 
static unsigned int n_dofs (const FEType &fet, const ElemType inf_elem_type)
 
static unsigned int n_dofs_at_node (const FEType &fet, const ElemType inf_elem_type, const unsigned int n)
 
static unsigned int n_dofs_per_elem (const FEType &fet, const ElemType inf_elem_type)
 
static void nodal_soln (const FEType &fet, const Elem *elem, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln)
 
static Point map (const Elem *inf_elem, const Point &reference_point)
 
static Point inverse_map (const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
 
static void inverse_map (const Elem *elem, const std::vector< Point > &physical_points, std::vector< Point > &reference_points, const Real tolerance=TOLERANCE, const bool secure=true)
 
static std::unique_ptr< FEGenericBase > build (const unsigned int dim, const FEType &type)
 
static std::unique_ptr< FEGenericBase > build_InfFE (const unsigned int dim, const FEType &type)
 
static void compute_proj_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem)
 
static void coarsened_dof_values (const NumericVector< Number > &global_vector, const DofMap &dof_map, const Elem *coarse_elem, DenseVector< Number > &coarse_dofs, const unsigned int var, const bool use_old_dof_indices=false)
 
static void coarsened_dof_values (const NumericVector< Number > &global_vector, const DofMap &dof_map, const Elem *coarse_elem, DenseVector< Number > &coarse_dofs, const bool use_old_dof_indices=false)
 
static void compute_periodic_constraints (DofConstraints &constraints, DofMap &dof_map, const PeriodicBoundaries &boundaries, const MeshBase &mesh, const PointLocatorBase *point_locator, const unsigned int variable_number, const Elem *elem)
 
static bool on_reference_element (const Point &p, const ElemType t, const Real eps=TOLERANCE)
 
static void get_refspace_nodes (const ElemType t, std::vector< Point > &nodes)
 
static void compute_node_constraints (NodeConstraints &constraints, const Elem *elem)
 
static void compute_periodic_node_constraints (NodeConstraints &constraints, const PeriodicBoundaries &boundaries, const MeshBase &mesh, const PointLocatorBase *point_locator, const Elem *elem)
 
static void print_info (std::ostream &out=libMesh::out)
 
static std::string get_info ()
 
static unsigned int n_objects ()
 
static void enable_print_counter_info ()
 
static void disable_print_counter_info ()
 

Protected Types

typedef std::map< std::string, std::pair< unsigned int, unsigned int > > Counts
 

Protected Member Functions

void update_base_elem (const Elem *inf_elem)
 
virtual void init_base_shape_functions (const std::vector< Point > &, const Elem *) override
 
void init_radial_shape_functions (const Elem *inf_elem, const std::vector< Point > *radial_pts=nullptr)
 
void init_shape_functions (const std::vector< Point > &radial_qp, const std::vector< Point > &base_qp, const Elem *inf_elem)
 
void init_face_shape_functions (const std::vector< Point > &qp, const Elem *side)
 
void combine_base_radial (const Elem *inf_elem)
 
virtual void compute_shape_functions (const Elem *, const std::vector< Point > &) override
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order o, unsigned i)
 
template<>
Real eval (Real v, Order o, unsigned i)
 
template<>
Real eval (Real v, Order o, unsigned i)
 
template<>
Real eval_deriv (Real v, Order o, unsigned i)
 
template<>
Real eval_deriv (Real v, Order o, unsigned i)
 
template<>
Real eval_deriv (Real v, Order o, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
template<>
Real eval_deriv (Real v, Order, unsigned i)
 
void determine_calculations ()
 
void increment_constructor_count (const std::string &name)
 
void increment_destructor_count (const std::string &name)
 

Static Protected Member Functions

static Real eval (Real v, Order o_radial, unsigned int i)
 
static Real eval_deriv (Real v, Order o_radial, unsigned int i)
 
static void compute_node_indices (const ElemType inf_elem_type, const unsigned int outer_node_index, unsigned int &base_node, unsigned int &radial_node)
 
static void compute_node_indices_fast (const ElemType inf_elem_type, const unsigned int outer_node_index, unsigned int &base_node, unsigned int &radial_node)
 
static void compute_shape_indices (const FEType &fet, const ElemType inf_elem_type, const unsigned int i, unsigned int &base_shape, unsigned int &radial_shape)
 

Protected Attributes

std::vector< Real > dist
 
std::vector< Real > dweightdv
 
std::vector< Real > som
 
std::vector< Real > dsomdv
 
std::vector< std::vector< Real > > mode
 
std::vector< std::vector< Real > > dmodedv
 
std::vector< std::vector< Real > > radial_map
 
std::vector< std::vector< Real > > dradialdv_map
 
std::vector< Real > dphasedxi
 
std::vector< Real > dphasedeta
 
std::vector< Real > dphasedzeta
 
std::vector< unsigned int > _radial_node_index
 
std::vector< unsigned int > _base_node_index
 
std::vector< unsigned int > _radial_shape_index
 
std::vector< unsigned int > _base_shape_index
 
unsigned int _n_total_approx_sf
 
unsigned int _n_total_qp
 
std::vector< Real > _total_qrule_weights
 
std::unique_ptr< QBase > base_qrule
 
std::unique_ptr< QBase > radial_qrule
 
std::unique_ptr< Elem > base_elem
 
std::unique_ptr< FEBase > base_fe
 
FEType current_fe_type
 
std::unique_ptr< FETransformationBase< OutputType > > _fe_trans
 
std::vector< std::vector< OutputShape > > phi
 
std::vector< std::vector< OutputGradient > > dphi
 
std::vector< std::vector< OutputShape > > curl_phi
 
std::vector< std::vector< OutputDivergence > > div_phi
 
std::vector< std::vector< OutputShape > > dphidxi
 
std::vector< std::vector< OutputShape > > dphideta
 
std::vector< std::vector< OutputShape > > dphidzeta
 
std::vector< std::vector< OutputShape > > dphidx
 
std::vector< std::vector< OutputShape > > dphidy
 
std::vector< std::vector< OutputShape > > dphidz
 
std::vector< std::vector< OutputTensor > > d2phi
 
std::vector< std::vector< OutputShape > > d2phidxi2
 
std::vector< std::vector< OutputShape > > d2phidxideta
 
std::vector< std::vector< OutputShape > > d2phidxidzeta
 
std::vector< std::vector< OutputShape > > d2phideta2
 
std::vector< std::vector< OutputShape > > d2phidetadzeta
 
std::vector< std::vector< OutputShape > > d2phidzeta2
 
std::vector< std::vector< OutputShape > > d2phidx2
 
std::vector< std::vector< OutputShape > > d2phidxdy
 
std::vector< std::vector< OutputShape > > d2phidxdz
 
std::vector< std::vector< OutputShape > > d2phidy2
 
std::vector< std::vector< OutputShape > > d2phidydz
 
std::vector< std::vector< OutputShape > > d2phidz2
 
std::vector< OutputGradient > dphase
 
std::vector< RealGradient > dweight
 
std::vector< Real > weight
 
std::unique_ptr< FEMap > _fe_map
 
const unsigned int dim
 
bool calculations_started
 
bool calculate_phi
 
bool calculate_dphi
 
bool calculate_d2phi
 
bool calculate_curl_phi
 
bool calculate_div_phi
 
bool calculate_dphiref
 
FEType fe_type
 
ElemType elem_type
 
unsigned int _p_level
 
QBase * qrule
 
bool shapes_on_quadrature
 

Static Protected Attributes

static Counts _counts
 
static Threads::atomic< unsigned int > _n_objects
 
static Threads::spin_mutex _mutex
 
static bool _enable_print_counter = true
 

Private Member Functions

virtual bool shapes_need_reinit () const override
 

Static Private Attributes

static ElemType _compute_node_indices_fast_current_elem_type = INVALID_ELEM
 
static bool _warned_for_nodal_soln = false
 
static bool _warned_for_shape = false
 

Friends

template<unsigned int friend_Dim, FEFamily friend_T_radial, InfMapType friend_T_map>
class InfFE
 

Detailed Description

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
class libMesh::InfFE< Dim, T_radial, T_map >

Base class for all the infinite geometric element types.

A specific instantiation of the FEBase class. This class is templated, and specific template instantiations will result in different Infinite Element families, similar to the FE class. InfFE builds a FE<Dim-1,T_base>, and most of the requests related to the base are handed over to this object. All methods related to the radial part are collected in the nested class Radial. Similarly, most of the static methods concerning base approximation are contained in Base.

Having different shape approximation families in radial direction introduces the requirement for an additional Order in this class. Therefore, the FEType internals change when infinite elements are enabled. When the specific infinite element type is not known at compile time, use the FEBase::build() member to create abstract (but still optimized) infinite elements at run time.

The node numbering scheme is the one from the current infinite element. Each node in the base holds exactly the same number of dofs as an adjacent conventional FE would contain. The nodes further out hold the additional dof necessary for radial approximation. The order of the outer nodes' components is such that the radial shapes have highest priority, followed by the base shapes.

Author
Daniel Dreyer
Date
2003

Definition at line 40 of file fe.h.

Member Typedef Documentation

◆ Counts

typedef std::map<std::string, std::pair<unsigned int, unsigned int> > libMesh::ReferenceCounter::Counts
protectedinherited

Data structure to log the information. The log is identified by the class name.

Definition at line 117 of file reference_counter.h.

◆ OutputDivergence

template<typename OutputType>
typedef TensorTools::DecrementRank<OutputShape>::type libMesh::FEGenericBase< OutputType >::OutputDivergence
inherited

Definition at line 122 of file fe_base.h.

◆ OutputGradient

template<typename OutputType>
typedef TensorTools::IncrementRank<OutputShape>::type libMesh::FEGenericBase< OutputType >::OutputGradient
inherited

Definition at line 120 of file fe_base.h.

◆ OutputNumber

template<typename OutputType>
typedef TensorTools::MakeNumber<OutputShape>::type libMesh::FEGenericBase< OutputType >::OutputNumber
inherited

Definition at line 123 of file fe_base.h.

◆ OutputNumberDivergence

template<typename OutputType>
typedef TensorTools::DecrementRank<OutputNumber>::type libMesh::FEGenericBase< OutputType >::OutputNumberDivergence
inherited

Definition at line 126 of file fe_base.h.

◆ OutputNumberGradient

template<typename OutputType>
typedef TensorTools::IncrementRank<OutputNumber>::type libMesh::FEGenericBase< OutputType >::OutputNumberGradient
inherited

Definition at line 124 of file fe_base.h.

◆ OutputNumberTensor

template<typename OutputType>
typedef TensorTools::IncrementRank<OutputNumberGradient>::type libMesh::FEGenericBase< OutputType >::OutputNumberTensor
inherited

Definition at line 125 of file fe_base.h.

◆ OutputShape

template<typename OutputType>
typedef OutputType libMesh::FEGenericBase< OutputType >::OutputShape
inherited

Convenient typedefs for gradients of output, hessians of output, and potentially-complex-valued versions of same.

Definition at line 119 of file fe_base.h.

◆ OutputTensor

template<typename OutputType>
typedef TensorTools::IncrementRank<OutputGradient>::type libMesh::FEGenericBase< OutputType >::OutputTensor
inherited

Definition at line 121 of file fe_base.h.

Constructor & Destructor Documentation

◆ InfFE()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
libMesh::InfFE< Dim, T_radial, T_map >::InfFE ( const FEType &  fet)
explicit

Constructor and empty destructor. Initializes some data structures. Builds a FE<Dim-1,T_base> object to handle approximation in the base, so that there is no need to template InfFE<Dim,T_radial,T_map> also with respect to the base approximation T_base.

The same remarks concerning compile-time optimization for FE also hold for InfFE. Use the FEBase::build_InfFE(const unsigned int, const FEType &) method to build specific instantiations of InfFE at run time.

Definition at line 37 of file inf_fe.C.

References libMesh::InfFE< Dim, T_radial, T_map >::base_fe, libMesh::FEGenericBase< OutputType >::build(), libMesh::FEAbstract::fe_type, libMesh::FEType::inf_map, and libMesh::FEType::radial_family.

37  :
38  FEBase (Dim, fet),
39 
40  _n_total_approx_sf (0),
41  _n_total_qp (0),
42 
43  // initialize the current_fe_type to all the same
44  // values as \p fet (since the FE families and coordinate
45  // map type should not change), but use an invalid order
46  // for the radial part (since this is the only order
47  // that may change!).
48  // the data structures like \p phi etc are not initialized
49  // through the constructor, but through reinit()
50  current_fe_type (FEType(fet.order,
51  fet.family,
52  INVALID_ORDER,
53  fet.radial_family,
54  fet.inf_map))
55 
56 {
57  // Sanity checks
58  libmesh_assert_equal_to (T_radial, fe_type.radial_family);
59  libmesh_assert_equal_to (T_map, fe_type.inf_map);
60 
61  // build the base_fe object
62  if (Dim != 1)
63  base_fe = FEBase::build(Dim-1, fet);
64 }
libMesh::InfFE::_n_total_qp
unsigned int _n_total_qp
Definition: inf_fe.h:740
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::FEGenericBase::build
static std::unique_ptr< FEGenericBase > build(const unsigned int dim, const FEType &type)
libMesh::FEType::inf_map
InfMapType inf_map
Definition: fe_type.h:258
libMesh::InfFE::current_fe_type
FEType current_fe_type
Definition: inf_fe.h:782
libMesh::FEBase
FEGenericBase< Real > FEBase
Definition: exact_error_estimator.h:39
libMesh::InfFE::_n_total_approx_sf
unsigned int _n_total_approx_sf
Definition: inf_fe.h:734
libMesh::FEType::radial_family
FEFamily radial_family
Definition: fe_type.h:250

◆ ~InfFE()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
libMesh::InfFE< Dim, T_radial, T_map >::~InfFE ( )
inline

Definition at line 245 of file inf_fe.h.

245 {}

Member Function Documentation

◆ attach_quadrature_rule()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::attach_quadrature_rule ( QBase *  q)
overridevirtual

The use of quadrature rules with the InfFE class is somewhat different from the approach of the FE class. While the FE class requires an appropriately initialized quadrature rule object, and simply uses it, the InfFE class requires only the quadrature rule object of the current FE class. From this QBase *, it determines the necessary data, and builds two appropriate quadrature classes, one for radial, and another for base integration, using the convenient QBase::build() method.

Implements libMesh::FEAbstract.

Definition at line 69 of file inf_fe.C.

References libMesh::QBase::build(), libMesh::QBase::get_dim(), libMesh::QBase::get_order(), and libMesh::QBase::type().

70 {
71  libmesh_assert(q);
72  libmesh_assert(base_fe);
73 
74  const Order base_int_order = q->get_order();
75  const Order radial_int_order = static_cast<Order>(2 * (static_cast<unsigned int>(fe_type.radial_order.get_order()) + 1) +2);
76  const unsigned int qrule_dim = q->get_dim();
77 
78  if (Dim != 1)
79  {
80  // build a Dim-1 quadrature rule of the type that we received
81  base_qrule = QBase::build(q->type(), qrule_dim-1, base_int_order);
82  base_fe->attach_quadrature_rule(base_qrule.get());
83  }
84 
85  // in radial direction, always use Gauss quadrature
86  radial_qrule.reset(new QGauss(1, radial_int_order));
87 
88  // currently not used. But maybe helpful to store the QBase *
89  // with which we initialized our own quadrature rules
90  qrule = q;
91 }
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::FEType::radial_order
OrderWrapper radial_order
Definition: fe_type.h:237
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::QBase::build
static std::unique_ptr< QBase > build(const std::string &name, const unsigned int dim, const Order order=INVALID_ORDER)
Definition: quadrature_build.C:40
libMesh::OrderWrapper::get_order
int get_order() const
Definition: fe_type.h:78
libMesh::InfFE::base_qrule
std::unique_ptr< QBase > base_qrule
Definition: inf_fe.h:752

◆ build() [1/3]

template<typename OutputType>
static std::unique_ptr<FEGenericBase> libMesh::FEGenericBase< OutputType >::build ( const unsigned int  dim,
const FEType &  type 
)
staticinherited

Builds a specific finite element type. A std::unique_ptr<FEGenericBase> is returned to prevent a memory leak. This way the user need not remember to delete the object.

The build call will fail if the OutputType of this class is not compatible with the output required for the requested type

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::UniformRefinementEstimator::_estimate_error(), libMesh::FEMContext::cached_fe(), libMesh::System::calculate_norm(), libMesh::MeshFunction::discontinuous_gradient(), libMesh::ExactErrorEstimator::estimate_error(), libMesh::MeshFunction::gradient(), libMesh::MeshFunction::hessian(), libMesh::InfFE< Dim, T_radial, T_map >::InfFE(), libMesh::InfFE< Dim, T_radial, T_map >::init_face_shape_functions(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), libMesh::WeightedPatchRecoveryErrorEstimator::EstimateError::operator()(), libMesh::PatchRecoveryErrorEstimator::EstimateError::operator()(), libMesh::System::point_gradient(), libMesh::System::point_hessian(), libMesh::InfFE< Dim, T_radial, T_map >::reinit(), libMesh::HPCoarsenTest::select_refinement(), and libMesh::Elem::volume().

◆ build() [2/3]

template<>
std::unique_ptr< FEGenericBase< Real > > libMesh::FEGenericBase< Real >::build ( const unsigned int  dim,
const FEType &  fet 
)
inherited

Definition at line 182 of file fe_base.C.

184 {
185  switch (dim)
186  {
187  // 0D
188  case 0:
189  {
190  switch (fet.family)
191  {
192  case CLOUGH:
193  return libmesh_make_unique<FE<0,CLOUGH>>(fet);
194 
195  case HERMITE:
196  return libmesh_make_unique<FE<0,HERMITE>>(fet);
197 
198  case LAGRANGE:
199  return libmesh_make_unique<FE<0,LAGRANGE>>(fet);
200 
201  case L2_LAGRANGE:
202  return libmesh_make_unique<FE<0,L2_LAGRANGE>>(fet);
203 
204  case HIERARCHIC:
205  return libmesh_make_unique<FE<0,HIERARCHIC>>(fet);
206 
207  case L2_HIERARCHIC:
208  return libmesh_make_unique<FE<0,L2_HIERARCHIC>>(fet);
209 
210  case MONOMIAL:
211  return libmesh_make_unique<FE<0,MONOMIAL>>(fet);
212 
213 #ifdef LIBMESH_ENABLE_HIGHER_ORDER_SHAPES
214  case SZABAB:
215  return libmesh_make_unique<FE<0,SZABAB>>(fet);
216 
217  case BERNSTEIN:
218  return libmesh_make_unique<FE<0,BERNSTEIN>>(fet);
219 #endif
220 
221  case XYZ:
222  return libmesh_make_unique<FEXYZ<0>>(fet);
223 
224  case SCALAR:
225  return libmesh_make_unique<FEScalar<0>>(fet);
226 
227  default:
228  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
229  }
230  }
231  // 1D
232  case 1:
233  {
234  switch (fet.family)
235  {
236  case CLOUGH:
237  return libmesh_make_unique<FE<1,CLOUGH>>(fet);
238 
239  case HERMITE:
240  return libmesh_make_unique<FE<1,HERMITE>>(fet);
241 
242  case LAGRANGE:
243  return libmesh_make_unique<FE<1,LAGRANGE>>(fet);
244 
245  case L2_LAGRANGE:
246  return libmesh_make_unique<FE<1,L2_LAGRANGE>>(fet);
247 
248  case HIERARCHIC:
249  return libmesh_make_unique<FE<1,HIERARCHIC>>(fet);
250 
251  case L2_HIERARCHIC:
252  return libmesh_make_unique<FE<1,L2_HIERARCHIC>>(fet);
253 
254  case MONOMIAL:
255  return libmesh_make_unique<FE<1,MONOMIAL>>(fet);
256 
257 #ifdef LIBMESH_ENABLE_HIGHER_ORDER_SHAPES
258  case SZABAB:
259  return libmesh_make_unique<FE<1,SZABAB>>(fet);
260 
261  case BERNSTEIN:
262  return libmesh_make_unique<FE<1,BERNSTEIN>>(fet);
263 #endif
264 
265  case XYZ:
266  return libmesh_make_unique<FEXYZ<1>>(fet);
267 
268  case SCALAR:
269  return libmesh_make_unique<FEScalar<1>>(fet);
270 
271  default:
272  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
273  }
274  }
275 
276 
277  // 2D
278  case 2:
279  {
280  switch (fet.family)
281  {
282  case CLOUGH:
283  return libmesh_make_unique<FE<2,CLOUGH>>(fet);
284 
285  case HERMITE:
286  return libmesh_make_unique<FE<2,HERMITE>>(fet);
287 
288  case LAGRANGE:
289  return libmesh_make_unique<FE<2,LAGRANGE>>(fet);
290 
291  case L2_LAGRANGE:
292  return libmesh_make_unique<FE<2,L2_LAGRANGE>>(fet);
293 
294  case HIERARCHIC:
295  return libmesh_make_unique<FE<2,HIERARCHIC>>(fet);
296 
297  case L2_HIERARCHIC:
298  return libmesh_make_unique<FE<2,L2_HIERARCHIC>>(fet);
299 
300  case MONOMIAL:
301  return libmesh_make_unique<FE<2,MONOMIAL>>(fet);
302 
303 #ifdef LIBMESH_ENABLE_HIGHER_ORDER_SHAPES
304  case SZABAB:
305  return libmesh_make_unique<FE<2,SZABAB>>(fet);
306 
307  case BERNSTEIN:
308  return libmesh_make_unique<FE<2,BERNSTEIN>>(fet);
309 #endif
310 
311  case XYZ:
312  return libmesh_make_unique<FEXYZ<2>>(fet);
313 
314  case SCALAR:
315  return libmesh_make_unique<FEScalar<2>>(fet);
316 
317  case SUBDIVISION:
318  return libmesh_make_unique<FESubdivision>(fet);
319 
320  default:
321  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
322  }
323  }
324 
325 
326  // 3D
327  case 3:
328  {
329  switch (fet.family)
330  {
331  case CLOUGH:
332  libmesh_error_msg("ERROR: Clough-Tocher elements currently only support 1D and 2D");
333 
334  case HERMITE:
335  return libmesh_make_unique<FE<3,HERMITE>>(fet);
336 
337  case LAGRANGE:
338  return libmesh_make_unique<FE<3,LAGRANGE>>(fet);
339 
340  case L2_LAGRANGE:
341  return libmesh_make_unique<FE<3,L2_LAGRANGE>>(fet);
342 
343  case HIERARCHIC:
344  return libmesh_make_unique<FE<3,HIERARCHIC>>(fet);
345 
346  case L2_HIERARCHIC:
347  return libmesh_make_unique<FE<3,L2_HIERARCHIC>>(fet);
348 
349  case MONOMIAL:
350  return libmesh_make_unique<FE<3,MONOMIAL>>(fet);
351 
352 #ifdef LIBMESH_ENABLE_HIGHER_ORDER_SHAPES
353  case SZABAB:
354  return libmesh_make_unique<FE<3,SZABAB>>(fet);
355 
356  case BERNSTEIN:
357  return libmesh_make_unique<FE<3,BERNSTEIN>>(fet);
358 #endif
359 
360  case XYZ:
361  return libmesh_make_unique<FEXYZ<3>>(fet);
362 
363  case SCALAR:
364  return libmesh_make_unique<FEScalar<3>>(fet);
365 
366  default:
367  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
368  }
369  }
370 
371  default:
372  libmesh_error_msg("Invalid dimension dim = " << dim);
373  }
374 }
libMesh::FEType::family
FEFamily family
Definition: fe_type.h:204
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531

◆ build() [3/3]

template<>
std::unique_ptr< FEGenericBase< RealGradient > > libMesh::FEGenericBase< RealGradient >::build ( const unsigned int  dim,
const FEType &  fet 
)
inherited

Definition at line 380 of file fe_base.C.

382 {
383  switch (dim)
384  {
385  // 0D
386  case 0:
387  {
388  switch (fet.family)
389  {
390  case LAGRANGE_VEC:
391  return libmesh_make_unique<FELagrangeVec<0>>(fet);
392 
393  default:
394  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
395  }
396  }
397  case 1:
398  {
399  switch (fet.family)
400  {
401  case LAGRANGE_VEC:
402  return libmesh_make_unique<FELagrangeVec<1>>(fet);
403 
404  default:
405  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
406  }
407  }
408  case 2:
409  {
410  switch (fet.family)
411  {
412  case LAGRANGE_VEC:
413  return libmesh_make_unique<FELagrangeVec<2>>(fet);
414 
415  case NEDELEC_ONE:
416  return libmesh_make_unique<FENedelecOne<2>>(fet);
417 
418  default:
419  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
420  }
421  }
422  case 3:
423  {
424  switch (fet.family)
425  {
426  case LAGRANGE_VEC:
427  return libmesh_make_unique<FELagrangeVec<3>>(fet);
428 
429  case NEDELEC_ONE:
430  return libmesh_make_unique<FENedelecOne<3>>(fet);
431 
432  default:
433  libmesh_error_msg("ERROR: Bad FEType.family= " << fet.family);
434  }
435  }
436 
437  default:
438  libmesh_error_msg("Invalid dimension dim = " << dim);
439  } // switch(dim)
440 }
libMesh::FEType::family
FEFamily family
Definition: fe_type.h:204
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531

◆ build_InfFE() [1/3]

template<typename OutputType>
static std::unique_ptr<FEGenericBase> libMesh::FEGenericBase< OutputType >::build_InfFE ( const unsigned int  dim,
const FEType &  type 
)
staticinherited

Builds a specific infinite element type. A std::unique_ptr<FEGenericBase> is returned to prevent a memory leak. This way the user need not remember to delete the object.

The build call will fail if the OutputShape of this class is not compatible with the output required for the requested type

Referenced by libMesh::FEMContext::cached_fe().

◆ build_InfFE() [2/3]

template<>
std::unique_ptr< FEGenericBase< Real > > libMesh::FEGenericBase< Real >::build_InfFE ( const unsigned int  dim,
const FEType &  fet 
)
inherited

Definition at line 453 of file fe_base.C.

455 {
456  switch (dim)
457  {
458 
459  // 1D
460  case 1:
461  {
462  switch (fet.radial_family)
463  {
464  case INFINITE_MAP:
465  libmesh_error_msg("ERROR: Can't build an infinite element with FEFamily = " << fet.radial_family);
466 
467  case JACOBI_20_00:
468  {
469  switch (fet.inf_map)
470  {
471  case CARTESIAN:
472  return libmesh_make_unique<InfFE<1,JACOBI_20_00,CARTESIAN>>(fet);
473 
474  default:
475  libmesh_error_msg("ERROR: Can't build an infinite element with InfMapType = " << fet.inf_map);
476  }
477  }
478 
479  case JACOBI_30_00:
480  {
481  switch (fet.inf_map)
482  {
483  case CARTESIAN:
484  return libmesh_make_unique<InfFE<1,JACOBI_30_00,CARTESIAN>>(fet);
485 
486  default:
487  libmesh_error_msg("ERROR: Can't build an infinite element with InfMapType = " << fet.inf_map);
488  }
489  }
490 
491  case LEGENDRE:
492  {
493  switch (fet.inf_map)
494  {
495  case CARTESIAN:
496  return libmesh_make_unique<InfFE<1,LEGENDRE,CARTESIAN>>(fet);
497 
498  default:
499  libmesh_error_msg("ERROR: Can't build an infinite element with InfMapType = " << fet.inf_map);
500  }
501  }
502 
503  case LAGRANGE:
504  {
505  switch (fet.inf_map)
506  {
507  case CARTESIAN:
508  return libmesh_make_unique<InfFE<1,LAGRANGE,CARTESIAN>>(fet);
509 
510  default:
511  libmesh_error_msg("ERROR: Can't build an infinite element with InfMapType = " << fet.inf_map);
512  }
513  }
514 
515  default:
516  libmesh_error_msg("ERROR: Bad FEType.radial_family= " << fet.radial_family);
517  }
518  }
519 
520 
521 
522 
523  // 2D
524  case 2:
525  {
526  switch (fet.radial_family)
527  {
528  case INFINITE_MAP:
529  libmesh_error_msg("ERROR: Can't build an infinite element with FEFamily = " << fet.radial_family);
530 
531  case JACOBI_20_00:
532  {
533  switch (fet.inf_map)
534  {
535  case CARTESIAN:
536  return libmesh_make_unique<InfFE<2,JACOBI_20_00,CARTESIAN>>(fet);
537 
538  default:
539  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
540  }
541  }
542 
543  case JACOBI_30_00:
544  {
545  switch (fet.inf_map)
546  {
547  case CARTESIAN:
548  return libmesh_make_unique<InfFE<2,JACOBI_30_00,CARTESIAN>>(fet);
549 
550  default:
551  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
552  }
553  }
554 
555  case LEGENDRE:
556  {
557  switch (fet.inf_map)
558  {
559  case CARTESIAN:
560  return libmesh_make_unique<InfFE<2,LEGENDRE,CARTESIAN>>(fet);
561 
562  default:
563  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
564  }
565  }
566 
567  case LAGRANGE:
568  {
569  switch (fet.inf_map)
570  {
571  case CARTESIAN:
572  return libmesh_make_unique<InfFE<2,LAGRANGE,CARTESIAN>>(fet);
573 
574  default:
575  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
576  }
577  }
578 
579  default:
580  libmesh_error_msg("ERROR: Bad FEType.radial_family= " << fet.radial_family);
581  }
582  }
583 
584 
585 
586 
587  // 3D
588  case 3:
589  {
590  switch (fet.radial_family)
591  {
592  case INFINITE_MAP:
593  libmesh_error_msg("ERROR: Don't build an infinite element with FEFamily = " << fet.radial_family);
594 
595  case JACOBI_20_00:
596  {
597  switch (fet.inf_map)
598  {
599  case CARTESIAN:
600  return libmesh_make_unique<InfFE<3,JACOBI_20_00,CARTESIAN>>(fet);
601 
602  default:
603  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
604  }
605  }
606 
607  case JACOBI_30_00:
608  {
609  switch (fet.inf_map)
610  {
611  case CARTESIAN:
612  return libmesh_make_unique<InfFE<3,JACOBI_30_00,CARTESIAN>>(fet);
613 
614  default:
615  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
616  }
617  }
618 
619  case LEGENDRE:
620  {
621  switch (fet.inf_map)
622  {
623  case CARTESIAN:
624  return libmesh_make_unique<InfFE<3,LEGENDRE,CARTESIAN>>(fet);
625 
626  default:
627  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
628  }
629  }
630 
631  case LAGRANGE:
632  {
633  switch (fet.inf_map)
634  {
635  case CARTESIAN:
636  return libmesh_make_unique<InfFE<3,LAGRANGE,CARTESIAN>>(fet);
637 
638  default:
639  libmesh_error_msg("ERROR: Don't build an infinite element with InfMapType = " << fet.inf_map);
640  }
641  }
642 
643  default:
644  libmesh_error_msg("ERROR: Bad FEType.radial_family= " << fet.radial_family);
645  }
646  }
647 
648  default:
649  libmesh_error_msg("Invalid dimension dim = " << dim);
650  }
651 }
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531
libMesh::FEType::inf_map
InfMapType inf_map
Definition: fe_type.h:258
libMesh::FEType::radial_family
FEFamily radial_family
Definition: fe_type.h:250

◆ build_InfFE() [3/3]

template<>
std::unique_ptr< FEGenericBase< RealGradient > > libMesh::FEGenericBase< RealGradient >::build_InfFE ( const unsigned int  ,
const FEType &   
)
inherited

Definition at line 657 of file fe_base.C.

659 {
660  // No vector types defined... YET.
661  libmesh_not_implemented();
662  return std::unique_ptr<FEVectorBase>();
663 }

◆ coarsened_dof_values() [1/2]

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::coarsened_dof_values ( const NumericVector< Number > &  global_vector,
const DofMap &  dof_map,
const Elem *  coarse_elem,
DenseVector< Number > &  coarse_dofs,
const unsigned int  var,
const bool  use_old_dof_indices = false 
)
staticinherited

Creates a local projection on coarse_elem, based on the DoF values in global_vector for it's children. Computes a vector of coefficients corresponding to dof_indices for only the single given var

Definition at line 791 of file fe_base.C.

Referenced by libMesh::JumpErrorEstimator::estimate_error(), and libMesh::ExactErrorEstimator::estimate_error().

797 {
798  // Side/edge local DOF indices
799  std::vector<unsigned int> new_side_dofs, old_side_dofs;
800 
801  // FIXME: what about 2D shells in 3D space?
802  unsigned int dim = elem->dim();
803 
804  // Cache n_children(); it's a virtual call but it's const.
805  const unsigned int n_children = elem->n_children();
806 
807  // We use local FE objects for now
808  // FIXME: we should use more, external objects instead for efficiency
809  const FEType & base_fe_type = dof_map.variable_type(var);
810  std::unique_ptr<FEGenericBase<OutputShape>> fe
811  (FEGenericBase<OutputShape>::build(dim, base_fe_type));
812  std::unique_ptr<FEGenericBase<OutputShape>> fe_coarse
813  (FEGenericBase<OutputShape>::build(dim, base_fe_type));
814 
815  std::unique_ptr<QBase> qrule (base_fe_type.default_quadrature_rule(dim));
816  std::unique_ptr<QBase> qedgerule (base_fe_type.default_quadrature_rule(1));
817  std::unique_ptr<QBase> qsiderule (base_fe_type.default_quadrature_rule(dim-1));
818  std::vector<Point> coarse_qpoints;
819 
820  // The values of the shape functions at the quadrature
821  // points
822  const std::vector<std::vector<OutputShape>> & phi_values =
823  fe->get_phi();
824  const std::vector<std::vector<OutputShape>> & phi_coarse =
825  fe_coarse->get_phi();
826 
827  // The gradients of the shape functions at the quadrature
828  // points on the child element.
829  const std::vector<std::vector<OutputGradient>> * dphi_values =
830  nullptr;
831  const std::vector<std::vector<OutputGradient>> * dphi_coarse =
832  nullptr;
833 
834  const FEContinuity cont = fe->get_continuity();
835 
836  if (cont == C_ONE)
837  {
838  const std::vector<std::vector<OutputGradient>> &
839  ref_dphi_values = fe->get_dphi();
840  dphi_values = &ref_dphi_values;
841  const std::vector<std::vector<OutputGradient>> &
842  ref_dphi_coarse = fe_coarse->get_dphi();
843  dphi_coarse = &ref_dphi_coarse;
844  }
845 
846  // The Jacobian * quadrature weight at the quadrature points
847  const std::vector<Real> & JxW =
848  fe->get_JxW();
849 
850  // The XYZ locations of the quadrature points on the
851  // child element
852  const std::vector<Point> & xyz_values =
853  fe->get_xyz();
854 
855 
856 
857  FEType fe_type = base_fe_type, temp_fe_type;
858  const ElemType elem_type = elem->type();
859  fe_type.order = static_cast<Order>(fe_type.order +
860  elem->max_descendant_p_level());
861 
862  // Number of nodes on parent element
863  const unsigned int n_nodes = elem->n_nodes();
864 
865  // Number of dofs on parent element
866  const unsigned int new_n_dofs =
867  FEInterface::n_dofs(dim, fe_type, elem_type);
868 
869  // Fixed vs. free DoFs on edge/face projections
870  std::vector<char> dof_is_fixed(new_n_dofs, false); // bools
871  std::vector<int> free_dof(new_n_dofs, 0);
872 
873  DenseMatrix<Real> Ke;
874  DenseVector<Number> Fe;
875  Ue.resize(new_n_dofs); Ue.zero();
876 
877 
878  // When coarsening, in general, we need a series of
879  // projections to ensure a unique and continuous
880  // solution. We start by interpolating nodes, then
881  // hold those fixed and project edges, then
882  // hold those fixed and project faces, then
883  // hold those fixed and project interiors
884 
885  // Copy node values first
886  {
887  std::vector<dof_id_type> node_dof_indices;
888  if (use_old_dof_indices)
889  dof_map.old_dof_indices (elem, node_dof_indices, var);
890  else
891  dof_map.dof_indices (elem, node_dof_indices, var);
892 
893  unsigned int current_dof = 0;
894  for (unsigned int n=0; n!= n_nodes; ++n)
895  {
896  // FIXME: this should go through the DofMap,
897  // not duplicate dof_indices code badly!
898  const unsigned int my_nc =
899  FEInterface::n_dofs_at_node (dim, fe_type,
900  elem_type, n);
901  if (!elem->is_vertex(n))
902  {
903  current_dof += my_nc;
904  continue;
905  }
906 
907  temp_fe_type = base_fe_type;
908  // We're assuming here that child n shares vertex n,
909  // which is wrong on non-simplices right now
910  // ... but this code isn't necessary except on elements
911  // where p refinement creates more vertex dofs; we have
912  // no such elements yet.
913  /*
914  if (elem->child_ptr(n)->p_level() < elem->p_level())
915  {
916  temp_fe_type.order =
917  static_cast<Order>(temp_fe_type.order +
918  elem->child_ptr(n)->p_level());
919  }
920  */
921  const unsigned int nc =
922  FEInterface::n_dofs_at_node (dim, temp_fe_type,
923  elem_type, n);
924  for (unsigned int i=0; i!= nc; ++i)
925  {
926  Ue(current_dof) =
927  old_vector(node_dof_indices[current_dof]);
928  dof_is_fixed[current_dof] = true;
929  current_dof++;
930  }
931  }
932  }
933 
934  // In 3D, project any edge values next
935  if (dim > 2 && cont != DISCONTINUOUS)
936  for (auto e : elem->edge_index_range())
937  {
938  FEInterface::dofs_on_edge(elem, dim, fe_type,
939  e, new_side_dofs);
940 
941  const unsigned int n_new_side_dofs =
942  cast_int<unsigned int>(new_side_dofs.size());
943 
944  // Some edge dofs are on nodes and already
945  // fixed, others are free to calculate
946  unsigned int free_dofs = 0;
947  for (unsigned int i=0; i != n_new_side_dofs; ++i)
948  if (!dof_is_fixed[new_side_dofs[i]])
949  free_dof[free_dofs++] = i;
950  Ke.resize (free_dofs, free_dofs); Ke.zero();
951  Fe.resize (free_dofs); Fe.zero();
952  // The new edge coefficients
953  DenseVector<Number> Uedge(free_dofs);
954 
955  // Add projection terms from each child sharing
956  // this edge
957  for (unsigned int c=0; c != n_children; ++c)
958  {
959  if (!elem->is_child_on_edge(c,e))
960  continue;
961  const Elem * child = elem->child_ptr(c);
962 
963  std::vector<dof_id_type> child_dof_indices;
964  if (use_old_dof_indices)
965  dof_map.old_dof_indices (child,
966  child_dof_indices, var);
967  else
968  dof_map.dof_indices (child,
969  child_dof_indices, var);
970  const unsigned int child_n_dofs =
971  cast_int<unsigned int>
972  (child_dof_indices.size());
973 
974  temp_fe_type = base_fe_type;
975  temp_fe_type.order =
976  static_cast<Order>(temp_fe_type.order +
977  child->p_level());
978 
979  FEInterface::dofs_on_edge(child, dim,
980  temp_fe_type, e, old_side_dofs);
981 
982  // Initialize both child and parent FE data
983  // on the child's edge
984  fe->attach_quadrature_rule (qedgerule.get());
985  fe->edge_reinit (child, e);
986  const unsigned int n_qp = qedgerule->n_points();
987 
988  FEInterface::inverse_map (dim, fe_type, elem,
989  xyz_values, coarse_qpoints);
990 
991  fe_coarse->reinit(elem, &coarse_qpoints);
992 
993  // Loop over the quadrature points
994  for (unsigned int qp=0; qp<n_qp; qp++)
995  {
996  // solution value at the quadrature point
997  OutputNumber fineval = libMesh::zero;
998  // solution grad at the quadrature point
999  OutputNumberGradient finegrad;
1000 
1001  // Sum the solution values * the DOF
1002  // values at the quadrature point to
1003  // get the solution value and gradient.
1004  for (unsigned int i=0; i<child_n_dofs;
1005  i++)
1006  {
1007  fineval +=
1008  (old_vector(child_dof_indices[i])*
1009  phi_values[i][qp]);
1010  if (cont == C_ONE)
1011  finegrad += (*dphi_values)[i][qp] *
1012  old_vector(child_dof_indices[i]);
1013  }
1014 
1015  // Form edge projection matrix
1016  for (unsigned int sidei=0, freei=0; sidei != n_new_side_dofs; ++sidei)
1017  {
1018  unsigned int i = new_side_dofs[sidei];
1019  // fixed DoFs aren't test functions
1020  if (dof_is_fixed[i])
1021  continue;
1022  for (unsigned int sidej=0, freej=0; sidej != n_new_side_dofs; ++sidej)
1023  {
1024  unsigned int j =
1025  new_side_dofs[sidej];
1026  if (dof_is_fixed[j])
1027  Fe(freei) -=
1028  TensorTools::inner_product(phi_coarse[i][qp],
1029  phi_coarse[j][qp]) *
1030  JxW[qp] * Ue(j);
1031  else
1032  Ke(freei,freej) +=
1033  TensorTools::inner_product(phi_coarse[i][qp],
1034  phi_coarse[j][qp]) *
1035  JxW[qp];
1036  if (cont == C_ONE)
1037  {
1038  if (dof_is_fixed[j])
1039  Fe(freei) -=
1040  TensorTools::inner_product((*dphi_coarse)[i][qp],
1041  (*dphi_coarse)[j][qp]) *
1042  JxW[qp] * Ue(j);
1043  else
1044  Ke(freei,freej) +=
1045  TensorTools::inner_product((*dphi_coarse)[i][qp],
1046  (*dphi_coarse)[j][qp]) *
1047  JxW[qp];
1048  }
1049  if (!dof_is_fixed[j])
1050  freej++;
1051  }
1052  Fe(freei) += TensorTools::inner_product(phi_coarse[i][qp],
1053  fineval) * JxW[qp];
1054  if (cont == C_ONE)
1055  Fe(freei) +=
1056  TensorTools::inner_product(finegrad, (*dphi_coarse)[i][qp]) * JxW[qp];
1057  freei++;
1058  }
1059  }
1060  }
1061  Ke.cholesky_solve(Fe, Uedge);
1062 
1063  // Transfer new edge solutions to element
1064  for (unsigned int i=0; i != free_dofs; ++i)
1065  {
1066  Number & ui = Ue(new_side_dofs[free_dof[i]]);
1067  libmesh_assert(std::abs(ui) < TOLERANCE ||
1068  std::abs(ui - Uedge(i)) < TOLERANCE);
1069  ui = Uedge(i);
1070  dof_is_fixed[new_side_dofs[free_dof[i]]] = true;
1071  }
1072  }
1073 
1074  // Project any side values (edges in 2D, faces in 3D)
1075  if (dim > 1 && cont != DISCONTINUOUS)
1076  for (auto s : elem->side_index_range())
1077  {
1078  FEInterface::dofs_on_side(elem, dim, fe_type,
1079  s, new_side_dofs);
1080 
1081  const unsigned int n_new_side_dofs =
1082  cast_int<unsigned int>(new_side_dofs.size());
1083 
1084  // Some side dofs are on nodes/edges and already
1085  // fixed, others are free to calculate
1086  unsigned int free_dofs = 0;
1087  for (unsigned int i=0; i != n_new_side_dofs; ++i)
1088  if (!dof_is_fixed[new_side_dofs[i]])
1089  free_dof[free_dofs++] = i;
1090  Ke.resize (free_dofs, free_dofs); Ke.zero();
1091  Fe.resize (free_dofs); Fe.zero();
1092  // The new side coefficients
1093  DenseVector<Number> Uside(free_dofs);
1094 
1095  // Add projection terms from each child sharing
1096  // this side
1097  for (unsigned int c=0; c != n_children; ++c)
1098  {
1099  if (!elem->is_child_on_side(c,s))
1100  continue;
1101  const Elem * child = elem->child_ptr(c);
1102 
1103  std::vector<dof_id_type> child_dof_indices;
1104  if (use_old_dof_indices)
1105  dof_map.old_dof_indices (child,
1106  child_dof_indices, var);
1107  else
1108  dof_map.dof_indices (child,
1109  child_dof_indices, var);
1110  const unsigned int child_n_dofs =
1111  cast_int<unsigned int>
1112  (child_dof_indices.size());
1113 
1114  temp_fe_type = base_fe_type;
1115  temp_fe_type.order =
1116  static_cast<Order>(temp_fe_type.order +
1117  child->p_level());
1118 
1119  FEInterface::dofs_on_side(child, dim,
1120  temp_fe_type, s, old_side_dofs);
1121 
1122  // Initialize both child and parent FE data
1123  // on the child's side
1124  fe->attach_quadrature_rule (qsiderule.get());
1125  fe->reinit (child, s);
1126  const unsigned int n_qp = qsiderule->n_points();
1127 
1128  FEInterface::inverse_map (dim, fe_type, elem,
1129  xyz_values, coarse_qpoints);
1130 
1131  fe_coarse->reinit(elem, &coarse_qpoints);
1132 
1133  // Loop over the quadrature points
1134  for (unsigned int qp=0; qp<n_qp; qp++)
1135  {
1136  // solution value at the quadrature point
1137  OutputNumber fineval = libMesh::zero;
1138  // solution grad at the quadrature point
1139  OutputNumberGradient finegrad;
1140 
1141  // Sum the solution values * the DOF
1142  // values at the quadrature point to
1143  // get the solution value and gradient.
1144  for (unsigned int i=0; i<child_n_dofs;
1145  i++)
1146  {
1147  fineval +=
1148  old_vector(child_dof_indices[i]) *
1149  phi_values[i][qp];
1150  if (cont == C_ONE)
1151  finegrad += (*dphi_values)[i][qp] *
1152  old_vector(child_dof_indices[i]);
1153  }
1154 
1155  // Form side projection matrix
1156  for (unsigned int sidei=0, freei=0; sidei != n_new_side_dofs; ++sidei)
1157  {
1158  unsigned int i = new_side_dofs[sidei];
1159  // fixed DoFs aren't test functions
1160  if (dof_is_fixed[i])
1161  continue;
1162  for (unsigned int sidej=0, freej=0; sidej != n_new_side_dofs; ++sidej)
1163  {
1164  unsigned int j =
1165  new_side_dofs[sidej];
1166  if (dof_is_fixed[j])
1167  Fe(freei) -=
1168  TensorTools::inner_product(phi_coarse[i][qp],
1169  phi_coarse[j][qp]) *
1170  JxW[qp] * Ue(j);
1171  else
1172  Ke(freei,freej) +=
1173  TensorTools::inner_product(phi_coarse[i][qp],
1174  phi_coarse[j][qp]) *
1175  JxW[qp];
1176  if (cont == C_ONE)
1177  {
1178  if (dof_is_fixed[j])
1179  Fe(freei) -=
1180  TensorTools::inner_product((*dphi_coarse)[i][qp],
1181  (*dphi_coarse)[j][qp]) *
1182  JxW[qp] * Ue(j);
1183  else
1184  Ke(freei,freej) +=
1185  TensorTools::inner_product((*dphi_coarse)[i][qp],
1186  (*dphi_coarse)[j][qp]) *
1187  JxW[qp];
1188  }
1189  if (!dof_is_fixed[j])
1190  freej++;
1191  }
1192  Fe(freei) += TensorTools::inner_product(fineval, phi_coarse[i][qp]) * JxW[qp];
1193  if (cont == C_ONE)
1194  Fe(freei) +=
1195  TensorTools::inner_product(finegrad, (*dphi_coarse)[i][qp]) * JxW[qp];
1196  freei++;
1197  }
1198  }
1199  }
1200  Ke.cholesky_solve(Fe, Uside);
1201 
1202  // Transfer new side solutions to element
1203  for (unsigned int i=0; i != free_dofs; ++i)
1204  {
1205  Number & ui = Ue(new_side_dofs[free_dof[i]]);
1206  libmesh_assert(std::abs(ui) < TOLERANCE ||
1207  std::abs(ui - Uside(i)) < TOLERANCE);
1208  ui = Uside(i);
1209  dof_is_fixed[new_side_dofs[free_dof[i]]] = true;
1210  }
1211  }
1212 
1213  // Project the interior values, finally
1214 
1215  // Some interior dofs are on nodes/edges/sides and
1216  // already fixed, others are free to calculate
1217  unsigned int free_dofs = 0;
1218  for (unsigned int i=0; i != new_n_dofs; ++i)
1219  if (!dof_is_fixed[i])
1220  free_dof[free_dofs++] = i;
1221  Ke.resize (free_dofs, free_dofs); Ke.zero();
1222  Fe.resize (free_dofs); Fe.zero();
1223  // The new interior coefficients
1224  DenseVector<Number> Uint(free_dofs);
1225 
1226  // Add projection terms from each child
1227  for (auto & child : elem->child_ref_range())
1228  {
1229  std::vector<dof_id_type> child_dof_indices;
1230  if (use_old_dof_indices)
1231  dof_map.old_dof_indices (&child,
1232  child_dof_indices, var);
1233  else
1234  dof_map.dof_indices (&child,
1235  child_dof_indices, var);
1236  const unsigned int child_n_dofs =
1237  cast_int<unsigned int>
1238  (child_dof_indices.size());
1239 
1240  // Initialize both child and parent FE data
1241  // on the child's quadrature points
1242  fe->attach_quadrature_rule (qrule.get());
1243  fe->reinit (&child);
1244  const unsigned int n_qp = qrule->n_points();
1245 
1246  FEInterface::inverse_map (dim, fe_type, elem,
1247  xyz_values, coarse_qpoints);
1248 
1249  fe_coarse->reinit(elem, &coarse_qpoints);
1250 
1251  // Loop over the quadrature points
1252  for (unsigned int qp=0; qp<n_qp; qp++)
1253  {
1254  // solution value at the quadrature point
1255  OutputNumber fineval = libMesh::zero;
1256  // solution grad at the quadrature point
1257  OutputNumberGradient finegrad;
1258 
1259  // Sum the solution values * the DOF
1260  // values at the quadrature point to
1261  // get the solution value and gradient.
1262  for (unsigned int i=0; i<child_n_dofs; i++)
1263  {
1264  fineval +=
1265  (old_vector(child_dof_indices[i]) *
1266  phi_values[i][qp]);
1267  if (cont == C_ONE)
1268  finegrad += (*dphi_values)[i][qp] *
1269  old_vector(child_dof_indices[i]);
1270  }
1271 
1272  // Form interior projection matrix
1273  for (unsigned int i=0, freei=0;
1274  i != new_n_dofs; ++i)
1275  {
1276  // fixed DoFs aren't test functions
1277  if (dof_is_fixed[i])
1278  continue;
1279  for (unsigned int j=0, freej=0; j !=
1280  new_n_dofs; ++j)
1281  {
1282  if (dof_is_fixed[j])
1283  Fe(freei) -=
1284  TensorTools::inner_product(phi_coarse[i][qp],
1285  phi_coarse[j][qp]) *
1286  JxW[qp] * Ue(j);
1287  else
1288  Ke(freei,freej) +=
1289  TensorTools::inner_product(phi_coarse[i][qp],
1290  phi_coarse[j][qp]) *
1291  JxW[qp];
1292  if (cont == C_ONE)
1293  {
1294  if (dof_is_fixed[j])
1295  Fe(freei) -=
1296  TensorTools::inner_product((*dphi_coarse)[i][qp],
1297  (*dphi_coarse)[j][qp]) *
1298  JxW[qp] * Ue(j);
1299  else
1300  Ke(freei,freej) +=
1301  TensorTools::inner_product((*dphi_coarse)[i][qp],
1302  (*dphi_coarse)[j][qp]) *
1303  JxW[qp];
1304  }
1305  if (!dof_is_fixed[j])
1306  freej++;
1307  }
1308  Fe(freei) += TensorTools::inner_product(phi_coarse[i][qp], fineval) *
1309  JxW[qp];
1310  if (cont == C_ONE)
1311  Fe(freei) += TensorTools::inner_product(finegrad, (*dphi_coarse)[i][qp]) * JxW[qp];
1312  freei++;
1313  }
1314  }
1315  }
1316  Ke.cholesky_solve(Fe, Uint);
1317 
1318  // Transfer new interior solutions to element
1319  for (unsigned int i=0; i != free_dofs; ++i)
1320  {
1321  Number & ui = Ue(free_dof[i]);
1322  libmesh_assert(std::abs(ui) < TOLERANCE ||
1323  std::abs(ui - Uint(i)) < TOLERANCE);
1324  ui = Uint(i);
1325  // We should be fixing all dofs by now; no need to keep track of
1326  // that unless we're debugging
1327 #ifndef NDEBUG
1328  dof_is_fixed[free_dof[i]] = true;
1329 #endif
1330  }
1331 
1332 #ifndef NDEBUG
1333  // Make sure every DoF got reached!
1334  for (unsigned int i=0; i != new_n_dofs; ++i)
1335  libmesh_assert(dof_is_fixed[i]);
1336 #endif
1337 }
libMesh::FEInterface::dofs_on_edge
static void dofs_on_edge(const Elem *const elem, const unsigned int dim, const FEType &fe_t, unsigned int e, std::vector< unsigned int > &di)
Definition: fe_interface.C:536
libMesh::FEType
Manages the family, order, etc. parameters for a given FE.
Definition: fe_type.h:179
std::abs
double abs(double a)
Definition: libmesh_augment_std_namespace.h:59
libMesh::FEInterface::n_dofs
static unsigned int n_dofs(const unsigned int dim, const FEType &fe_t, const ElemType t)
Definition: fe_interface.C:454
libMesh::DofMap::dof_indices
void dof_indices(const Elem *const elem, std::vector< dof_id_type > &di) const
Definition: dof_map.C:1930
libMesh::FEInterface::dofs_on_side
static void dofs_on_side(const Elem *const elem, const unsigned int dim, const FEType &fe_t, unsigned int s, std::vector< unsigned int > &di)
Definition: fe_interface.C:523
libMesh::DenseVector::resize
void resize(const unsigned int n)
Definition: dense_vector.h:355
libMesh::DofMap::variable_type
const FEType & variable_type(const unsigned int c) const
Definition: dof_map.h:1792
libMesh::Elem
The base class for all geometric element types.
Definition: elem.h:100
libMesh::FEGenericBase::OutputNumberGradient
TensorTools::IncrementRank< OutputNumber >::type OutputNumberGradient
Definition: fe_base.h:124
libMesh::Elem::p_level
unsigned int p_level() const
Definition: elem.h:2555
libMesh::FEType::order
OrderWrapper order
Definition: fe_type.h:198
libMesh::TOLERANCE
static const Real TOLERANCE
Definition: libmesh_common.h:139
libMesh::zero
const Number zero
Definition: libmesh.h:239
libMesh::DofMap::old_dof_indices
void old_dof_indices(const Elem *const elem, std::vector< dof_id_type > &di, const unsigned int vn=libMesh::invalid_uint) const
Definition: dof_map.C:2434
libMesh::FEType::default_quadrature_rule
std::unique_ptr< QBase > default_quadrature_rule(const unsigned int dim, const int extraorder=0) const
Definition: fe_type.C:31
n_nodes
const dof_id_type n_nodes
Definition: tecplot_io.C:68
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531
libMesh::FEInterface::inverse_map
static Point inverse_map(const unsigned int dim, const FEType &fe_t, const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: fe_interface.C:590
libMesh::QBase::n_points
unsigned int n_points() const
Definition: quadrature.h:127
libMesh::FEGenericBase::OutputNumber
TensorTools::MakeNumber< OutputShape >::type OutputNumber
Definition: fe_base.h:123
libMesh::FEInterface::n_dofs_at_node
static unsigned int n_dofs_at_node(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int n)
Definition: fe_interface.C:473
libMesh::DenseMatrix::zero
virtual void zero() override
Definition: dense_matrix.h:808
libMesh::DenseMatrix::resize
void resize(const unsigned int new_m, const unsigned int new_n)
Definition: dense_matrix.h:792
libMesh::DenseMatrix::cholesky_solve
void cholesky_solve(const DenseVector< T2 > &b, DenseVector< T2 > &x)
Definition: dense_matrix_impl.h:929
libMesh::DenseMatrix
A matrix object used for finite element assembly and numerics.
Definition: dense_matrix.h:54
libMesh::TensorTools::inner_product
boostcopy::enable_if_c< ScalarTraits< T >::value &&ScalarTraits< T2 >::value, typename CompareTypes< T, T2 >::supertype >::type inner_product(const T &a, const T2 &b)
Definition: tensor_tools.h:47
libMesh::Elem::child_ptr
const Elem * child_ptr(unsigned int i) const
Definition: elem.h:2578
libMesh::DenseVector::zero
virtual void zero() override
Definition: dense_vector.h:379

◆ coarsened_dof_values() [2/2]

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::coarsened_dof_values ( const NumericVector< Number > &  global_vector,
const DofMap &  dof_map,
const Elem *  coarse_elem,
DenseVector< Number > &  coarse_dofs,
const bool  use_old_dof_indices = false 
)
staticinherited

Creates a local projection on coarse_elem, based on the DoF values in global_vector for it's children. Computes a vector of coefficients corresponding to all dof_indices.

Definition at line 1343 of file fe_base.C.

1348 {
1349  Ue.resize(0);
1350 
1351  for (unsigned int v=0; v != dof_map.n_variables(); ++v)
1352  {
1353  DenseVector<Number> Usub;
1354 
1355  coarsened_dof_values(old_vector, dof_map, elem, Usub,
1356  use_old_dof_indices);
1357 
1358  Ue.append (Usub);
1359  }
1360 }
libMesh::DofMap::n_variables
unsigned int n_variables() const
Definition: dof_map.h:541
libMesh::FEGenericBase::coarsened_dof_values
static void coarsened_dof_values(const NumericVector< Number > &global_vector, const DofMap &dof_map, const Elem *coarse_elem, DenseVector< Number > &coarse_dofs, const unsigned int var, const bool use_old_dof_indices=false)
Definition: fe_base.C:791

◆ combine_base_radial()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::combine_base_radial ( const Elem *  inf_elem)
protected

Combines the shape functions, which were formed in init_shape_functions(Elem *), with geometric data. Has to be called every time the geometric configuration changes. Afterward, the fields are ready to be used to compute global derivatives, the jacobian etc, see FEAbstract::compute_map().

Definition at line 733 of file inf_fe.C.

References libMesh::Elem::origin(), and libMesh::Elem::type().

734 {
735  libmesh_assert(inf_elem);
736  // at least check whether the base element type is correct.
737  // otherwise this version of computing dist would give problems
738  libmesh_assert_equal_to (base_elem->type(), Base::get_elem_type(inf_elem->type()));
739 
740  // Start logging the combination of radial and base parts
741  LOG_SCOPE("combine_base_radial()", "InfFE");
742 
743  // zero the phase, since it is to be summed up
744  std::fill (dphasedxi.begin(), dphasedxi.end(), 0.);
745  std::fill (dphasedeta.begin(), dphasedeta.end(), 0.);
746  std::fill (dphasedzeta.begin(), dphasedzeta.end(), 0.);
747 
748 
749  const unsigned int n_base_mapping_sf = cast_int<unsigned int>(dist.size());
750  const Point origin = inf_elem->origin();
751 
752  // for each new infinite element, compute the radial distances
753  for (unsigned int n=0; n<n_base_mapping_sf; n++)
754  dist[n] = Point(base_elem->point(n) - origin).norm();
755 
756 
757  switch (Dim)
758  {
759  // 1D
760  case 1:
761  {
762  libmesh_not_implemented();
763  break;
764  }
765 
766  // 2D
767  case 2:
768  {
769  libmesh_not_implemented();
770  break;
771  }
772 
773  // 3D
774  case 3:
775  {
776  // fast access to the approximation and mapping shapes of base_fe
777  const std::vector<std::vector<Real>> & S = base_fe->phi;
778  const std::vector<std::vector<Real>> & Ss = base_fe->dphidxi;
779  const std::vector<std::vector<Real>> & St = base_fe->dphideta;
780  const std::vector<std::vector<Real>> & S_map = (base_fe->get_fe_map()).get_phi_map();
781  const std::vector<std::vector<Real>> & Ss_map = (base_fe->get_fe_map()).get_dphidxi_map();
782  const std::vector<std::vector<Real>> & St_map = (base_fe->get_fe_map()).get_dphideta_map();
783 
784  const unsigned int n_radial_qp = cast_int<unsigned int>(som.size());
785  if (radial_qrule)
786  libmesh_assert_equal_to(n_radial_qp, radial_qrule->n_points());
787  const unsigned int n_base_qp = cast_int<unsigned int>(S_map[0].size());
788  if (base_qrule)
789  libmesh_assert_equal_to(n_base_qp, base_qrule->n_points());
790 
791  const unsigned int n_total_mapping_sf =
792  cast_int<unsigned int>(radial_map.size()) * n_base_mapping_sf;
793 
794  const unsigned int n_total_approx_sf = Radial::n_dofs(fe_type.radial_order) * base_fe->n_shape_functions();
795 
796 
797  // compute the phase term derivatives
798  {
799  unsigned int tp=0;
800  for (unsigned int rp=0; rp<n_radial_qp; rp++) // over radial qps
801  for (unsigned int bp=0; bp<n_base_qp; bp++) // over base qps
802  {
803  // sum over all base shapes, to get the average distance
804  for (unsigned int i=0; i<n_base_mapping_sf; i++)
805  {
806  dphasedxi[tp] += Ss_map[i][bp] * dist[i] * radial_map [1][rp];
807  dphasedeta[tp] += St_map[i][bp] * dist[i] * radial_map [1][rp];
808  dphasedzeta[tp] += S_map [i][bp] * dist[i] * dradialdv_map[1][rp];
809  }
810 
811  tp++;
812 
813  } // loop radial and base qps
814  }
815 
816  libmesh_assert_equal_to (phi.size(), n_total_approx_sf);
817  libmesh_assert_equal_to (dphidxi.size(), n_total_approx_sf);
818  libmesh_assert_equal_to (dphideta.size(), n_total_approx_sf);
819  libmesh_assert_equal_to (dphidzeta.size(), n_total_approx_sf);
820 
821  // compute the overall approximation shape functions,
822  // pick the appropriate radial and base shapes through using
823  // _base_shape_index and _radial_shape_index
824  for (unsigned int rp=0; rp<n_radial_qp; rp++) // over radial qps
825  for (unsigned int bp=0; bp<n_base_qp; bp++) // over base qps
826  for (unsigned int ti=0; ti<n_total_approx_sf; ti++) // over _all_ approx_sf
827  {
828  // let the index vectors take care of selecting the appropriate base/radial shape
829  const unsigned int bi = _base_shape_index [ti];
830  const unsigned int ri = _radial_shape_index[ti];
831  phi [ti][bp+rp*n_base_qp] = S [bi][bp] * mode[ri][rp] * som[rp];
832  dphidxi [ti][bp+rp*n_base_qp] = Ss[bi][bp] * mode[ri][rp] * som[rp];
833  dphideta [ti][bp+rp*n_base_qp] = St[bi][bp] * mode[ri][rp] * som[rp];
834  dphidzeta[ti][bp+rp*n_base_qp] = S [bi][bp]
835  * (dmodedv[ri][rp] * som[rp] + mode[ri][rp] * dsomdv[rp]);
836  }
837 
838  std::vector<std::vector<Real>> & phi_map = this->_fe_map->get_phi_map();
839  std::vector<std::vector<Real>> & dphidxi_map = this->_fe_map->get_dphidxi_map();
840  std::vector<std::vector<Real>> & dphideta_map = this->_fe_map->get_dphideta_map();
841  std::vector<std::vector<Real>> & dphidzeta_map = this->_fe_map->get_dphidzeta_map();
842 
843  libmesh_assert_equal_to (phi_map.size(), n_total_mapping_sf);
844  libmesh_assert_equal_to (dphidxi_map.size(), n_total_mapping_sf);
845  libmesh_assert_equal_to (dphideta_map.size(), n_total_mapping_sf);
846  libmesh_assert_equal_to (dphidzeta_map.size(), n_total_mapping_sf);
847 
848  // compute the overall mapping functions,
849  // pick the appropriate radial and base entries through using
850  // _base_node_index and _radial_node_index
851  for (unsigned int rp=0; rp<n_radial_qp; rp++) // over radial qps
852  for (unsigned int bp=0; bp<n_base_qp; bp++) // over base qps
853  for (unsigned int ti=0; ti<n_total_mapping_sf; ti++) // over all mapping shapes
854  {
855  // let the index vectors take care of selecting the appropriate base/radial mapping shape
856  const unsigned int bi = _base_node_index [ti];
857  const unsigned int ri = _radial_node_index[ti];
858  phi_map [ti][bp+rp*n_base_qp] = S_map [bi][bp] * radial_map [ri][rp];
859  dphidxi_map [ti][bp+rp*n_base_qp] = Ss_map[bi][bp] * radial_map [ri][rp];
860  dphideta_map [ti][bp+rp*n_base_qp] = St_map[bi][bp] * radial_map [ri][rp];
861  dphidzeta_map[ti][bp+rp*n_base_qp] = S_map [bi][bp] * dradialdv_map[ri][rp];
862  }
863 
864  break;
865  }
866 
867  default:
868  libmesh_error_msg("Unsupported Dim = " << Dim);
869  }
870 }
libMesh::FEGenericBase::dphidxi
std::vector< std::vector< OutputShape > > dphidxi
Definition: fe_base.h:518
libMesh::FEGenericBase::dphidzeta
std::vector< std::vector< OutputShape > > dphidzeta
Definition: fe_base.h:528
libMesh::InfFE::dsomdv
std::vector< Real > dsomdv
Definition: inf_fe.h:634
libMesh::InfFE::dradialdv_map
std::vector< std::vector< Real > > dradialdv_map
Definition: inf_fe.h:657
libMesh::InfFE::radial_map
std::vector< std::vector< Real > > radial_map
Definition: inf_fe.h:651
libMesh::InfFE::dphasedxi
std::vector< Real > dphasedxi
Definition: inf_fe.h:664
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::InfFE::_base_node_index
std::vector< unsigned int > _base_node_index
Definition: inf_fe.h:703
libMesh::FEType::radial_order
OrderWrapper radial_order
Definition: fe_type.h:237
libMesh::InfFE::Base::get_elem_type
static ElemType get_elem_type(const ElemType type)
Definition: inf_fe_base_radial.C:51
libMesh::InfFE::mode
std::vector< std::vector< Real > > mode
Definition: inf_fe.h:640
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::InfFE::dphasedzeta
std::vector< Real > dphasedzeta
Definition: inf_fe.h:678
libMesh::InfFE::dphasedeta
std::vector< Real > dphasedeta
Definition: inf_fe.h:671
libMesh::InfFE::Radial::n_dofs
static unsigned int n_dofs(const Order o_radial)
Definition: inf_fe.h:147
libMesh::InfFE::_radial_node_index
std::vector< unsigned int > _radial_node_index
Definition: inf_fe.h:693
libMesh::InfFE::som
std::vector< Real > som
Definition: inf_fe.h:629
libMesh::InfFE::base_qrule
std::unique_ptr< QBase > base_qrule
Definition: inf_fe.h:752
libMesh::InfFE::_radial_shape_index
std::vector< unsigned int > _radial_shape_index
Definition: inf_fe.h:713
libMesh::InfFE::_base_shape_index
std::vector< unsigned int > _base_shape_index
Definition: inf_fe.h:723
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525
libMesh::InfFE::dist
std::vector< Real > dist
Definition: inf_fe.h:612
libMesh::InfFE::dmodedv
std::vector< std::vector< Real > > dmodedv
Definition: inf_fe.h:646
libMesh::FEGenericBase::dphideta
std::vector< std::vector< OutputShape > > dphideta
Definition: fe_base.h:523

◆ compute_data()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::compute_data ( const FEType &  fe_t,
const Elem *  inf_elem,
FEComputeData &  data 
)
static

Generalized version of shape(), takes an Elem *. The data contains both input and output parameters. For frequency domain simulations, the complex-valued shape is returned. In time domain both the computed shape, and the phase is returned.

Note
The phase (proportional to the distance of the Point data.p from the envelope) is actually a measure how far into the future the results are.

Definition at line 241 of file inf_fe_static.C.

References libMesh::Elem::build_side_ptr(), data, libMesh::InfFE< Dim, T_radial, T_map >::Radial::decay(), libMesh::InfFE< Dim, T_radial, T_map >::eval(), libMesh::imaginary, libMesh::INFEDGE2, libMesh::Elem::origin(), libMesh::pi, libMesh::Elem::point(), libMesh::FEType::radial_order, libMesh::Real, libMesh::FE< Dim, T >::shape(), libMesh::FEInterface::shape(), and libMesh::Elem::type().

Referenced by libMesh::FEInterface::ifem_compute_data().

244 {
245  libmesh_assert(inf_elem);
246  libmesh_assert_not_equal_to (Dim, 0);
247 
248  const Order o_radial (fet.radial_order);
249  const Order radial_mapping_order (Radial::mapping_order());
250  const Point & p (data.p);
251  const Real v (p(Dim-1));
252  std::unique_ptr<const Elem> base_el (inf_elem->build_side_ptr(0));
253 
254  /*
255  * compute \p interpolated_dist containing the mapping-interpolated
256  * distance of the base point to the origin. This is the same
257  * for all shape functions. Set \p interpolated_dist to 0, it
258  * is added to.
259  */
260  Real interpolated_dist = 0.;
261  switch (Dim)
262  {
263  case 1:
264  {
265  libmesh_assert_equal_to (inf_elem->type(), INFEDGE2);
266  interpolated_dist = Point(inf_elem->point(0) - inf_elem->point(1)).norm();
267  break;
268  }
269 
270  case 2:
271  {
272  const unsigned int n_base_nodes = base_el->n_nodes();
273 
274  const Point origin = inf_elem->origin();
275  const Order base_mapping_order (base_el->default_order());
276  const ElemType base_mapping_elem_type (base_el->type());
277 
278  // interpolate the base nodes' distances
279  for (unsigned int n=0; n<n_base_nodes; n++)
280  interpolated_dist += Point(base_el->point(n) - origin).norm()
281  * FE<1,LAGRANGE>::shape (base_mapping_elem_type, base_mapping_order, n, p);
282  break;
283  }
284 
285  case 3:
286  {
287  const unsigned int n_base_nodes = base_el->n_nodes();
288 
289  const Point origin = inf_elem->origin();
290  const Order base_mapping_order (base_el->default_order());
291  const ElemType base_mapping_elem_type (base_el->type());
292 
293  // interpolate the base nodes' distances
294  for (unsigned int n=0; n<n_base_nodes; n++)
295  interpolated_dist += Point(base_el->point(n) - origin).norm()
296  * FE<2,LAGRANGE>::shape (base_mapping_elem_type, base_mapping_order, n, p);
297  break;
298  }
299 
300  default:
301  libmesh_error_msg("Unknown Dim = " << Dim);
302  }
303 
304 
305  const Real speed = data.speed;
306 
307  //TODO: I find it inconvenient to have a quantity phase which is phase/speed.
308  // But it might be better than redefining a quantities meaning.
309  data.phase = interpolated_dist /* together with next line: */
310  * InfFE<Dim,INFINITE_MAP,T_map>::eval(v, radial_mapping_order, 1)/speed; /* phase(s,t,v)/c */
311 
312  // We assume time-harmonic behavior in this function!
313 
314 #ifdef LIBMESH_USE_COMPLEX_NUMBERS
315  // the wave number
316  const Number wavenumber = 2. * libMesh::pi * data.frequency / speed;
317 
318  // the exponent for time-harmonic behavior
319  // \note: this form is much less general than the implementation of dphase, which can be easily extended to
320  // other forms than e^{i kr}.
321  const Number exponent = imaginary /* imaginary unit */
322  * wavenumber /* k (can be complex) */
323  * data.phase*speed;
324 
325  const Number time_harmonic = exp(exponent); /* e^(i*k*phase(s,t,v)) */
326 #else
327  const Number time_harmonic = 1;
328 #endif //LIBMESH_USE_COMPLEX_NUMBERS
329 
330  /*
331  * compute \p shape for all dof in the element
332  */
333  if (Dim > 1)
334  {
335  const unsigned int n_dof = n_dofs (fet, inf_elem->type());
336  data.shape.resize(n_dof);
337 
338  for (unsigned int i=0; i<n_dof; i++)
339  {
340  // compute base and radial shape indices
341  unsigned int i_base, i_radial;
342  compute_shape_indices(fet, inf_elem->type(), i, i_base, i_radial);
343 
344  data.shape[i] = (InfFE<Dim,T_radial,T_map>::Radial::decay(v) /* (1.-v)/2. in 3D */
345  * FEInterface::shape(Dim-1, fet, base_el.get(), i_base, p) /* S_n(s,t) */
346  * InfFE<Dim,T_radial,T_map>::eval(v, o_radial, i_radial)) /* L_n(v) */
347  * time_harmonic; /* e^(i*k*phase(s,t,v) */
348  }
349  }
350 
351  else
352  libmesh_error_msg("compute_data() for 1-dimensional InfFE not implemented.");
353 }
libMesh::FE::shape
static OutputShape shape(const ElemType t, const Order o, const unsigned int i, const Point &p)
libMesh::imaginary
const Number imaginary
libMesh::InfFE::n_dofs
static unsigned int n_dofs(const FEType &fet, const ElemType inf_elem_type)
Definition: inf_fe_static.C:55
libMesh::InfFE::Radial::decay
static Real decay(const Real v)
Definition: inf_fe.h:827
libMesh::FEInterface::shape
static Real shape(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int i, const Point &p)
Definition: fe_interface.C:657
libMesh::InfFE::eval
static Real eval(Real v, Order o_radial, unsigned int i)
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::InfFE::compute_shape_indices
static void compute_shape_indices(const FEType &fet, const ElemType inf_elem_type, const unsigned int i, unsigned int &base_shape, unsigned int &radial_shape)
Definition: inf_fe_static.C:677
data
IterBase * data
Definition: variant_filter_iterator.h:337
libMesh::InfFE::Radial::mapping_order
static Order mapping_order()
Definition: inf_fe.h:131
libMesh::pi
const Real pi
Definition: libmesh.h:233

◆ compute_node_constraints()

void libMesh::FEAbstract::compute_node_constraints ( NodeConstraints &  constraints,
const Elem *  elem 
)
staticinherited

Computes the nodal constraint contributions (for non-conforming adapted meshes), using Lagrange geometry

Definition at line 820 of file fe_abstract.C.

References std::abs(), libMesh::Elem::build_side_ptr(), libMesh::Elem::default_order(), libMesh::Elem::dim(), libMesh::FEAbstract::fe_type, libMesh::FEInterface::inverse_map(), libMesh::LAGRANGE, libMesh::Elem::level(), libMesh::FEInterface::n_dofs(), libMesh::Elem::neighbor_ptr(), libMesh::Elem::parent(), libMesh::Real, libMesh::remote_elem, libMesh::FEInterface::shape(), libMesh::Elem::side_index_range(), libMesh::Threads::spin_mtx, and libMesh::Elem::subactive().

822 {
823  libmesh_assert(elem);
824 
825  const unsigned int Dim = elem->dim();
826 
827  // Only constrain elements in 2,3D.
828  if (Dim == 1)
829  return;
830 
831  // Only constrain active and ancestor elements
832  if (elem->subactive())
833  return;
834 
835  // We currently always use LAGRANGE mappings for geometry
836  const FEType fe_type(elem->default_order(), LAGRANGE);
837 
838  // Pull objects out of the loop to reduce heap operations
839  std::vector<const Node *> my_nodes, parent_nodes;
840  std::unique_ptr<const Elem> my_side, parent_side;
841 
842  // Look at the element faces. Check to see if we need to
843  // build constraints.
844  for (auto s : elem->side_index_range())
845  if (elem->neighbor_ptr(s) != nullptr &&
846  elem->neighbor_ptr(s) != remote_elem)
847  if (elem->neighbor_ptr(s)->level() < elem->level()) // constrain dofs shared between
848  { // this element and ones coarser
849  // than this element.
850  // Get pointers to the elements of interest and its parent.
851  const Elem * parent = elem->parent();
852 
853  // This can't happen... Only level-0 elements have nullptr
854  // parents, and no level-0 elements can be at a higher
855  // level than their neighbors!
856  libmesh_assert(parent);
857 
858  elem->build_side_ptr(my_side, s);
859  parent->build_side_ptr(parent_side, s);
860 
861  const unsigned int n_side_nodes = my_side->n_nodes();
862 
863  my_nodes.clear();
864  my_nodes.reserve (n_side_nodes);
865  parent_nodes.clear();
866  parent_nodes.reserve (n_side_nodes);
867 
868  for (unsigned int n=0; n != n_side_nodes; ++n)
869  my_nodes.push_back(my_side->node_ptr(n));
870 
871  for (unsigned int n=0; n != n_side_nodes; ++n)
872  parent_nodes.push_back(parent_side->node_ptr(n));
873 
874  for (unsigned int my_side_n=0;
875  my_side_n < n_side_nodes;
876  my_side_n++)
877  {
878  libmesh_assert_less (my_side_n, FEInterface::n_dofs(Dim-1, fe_type, my_side->type()));
879 
880  const Node * my_node = my_nodes[my_side_n];
881 
882  // The support point of the DOF
883  const Point & support_point = *my_node;
884 
885  // Figure out where my node lies on their reference element.
886  const Point mapped_point = FEInterface::inverse_map(Dim-1, fe_type,
887  parent_side.get(),
888  support_point);
889 
890  // Compute the parent's side shape function values.
891  for (unsigned int their_side_n=0;
892  their_side_n < n_side_nodes;
893  their_side_n++)
894  {
895  libmesh_assert_less (their_side_n, FEInterface::n_dofs(Dim-1, fe_type, parent_side->type()));
896 
897  const Node * their_node = parent_nodes[their_side_n];
898  libmesh_assert(their_node);
899 
900  const Real their_value = FEInterface::shape(Dim-1,
901  fe_type,
902  parent_side->type(),
903  their_side_n,
904  mapped_point);
905 
906  const Real their_mag = std::abs(their_value);
907 #ifdef DEBUG
908  // Protect for the case u_i ~= u_j,
909  // in which case i better equal j.
910  if (their_mag > 0.999)
911  {
912  libmesh_assert_equal_to (my_node, their_node);
913  libmesh_assert_less (std::abs(their_value - 1.), 0.001);
914  }
915  else
916 #endif
917  // To make nodal constraints useful for constructing
918  // sparsity patterns faster, we need to get EVERY
919  // POSSIBLE constraint coupling identified, even if
920  // there is no coupling in the isoparametric
921  // Lagrange case.
922  if (their_mag < 1.e-5)
923  {
924  // since we may be running this method concurrently
925  // on multiple threads we need to acquire a lock
926  // before modifying the shared constraint_row object.
927  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
928 
929  // A reference to the constraint row.
930  NodeConstraintRow & constraint_row = constraints[my_node].first;
931 
932  constraint_row.insert(std::make_pair (their_node,
933  0.));
934  }
935  // To get nodal coordinate constraints right, only
936  // add non-zero and non-identity values for Lagrange
937  // basis functions.
938  else // (1.e-5 <= their_mag <= .999)
939  {
940  // since we may be running this method concurrently
941  // on multiple threads we need to acquire a lock
942  // before modifying the shared constraint_row object.
943  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
944 
945  // A reference to the constraint row.
946  NodeConstraintRow & constraint_row = constraints[my_node].first;
947 
948  constraint_row.insert(std::make_pair (their_node,
949  their_value));
950  }
951  }
952  }
953  }
954 }
std::abs
double abs(double a)
Definition: libmesh_augment_std_namespace.h:59
libMesh::FEInterface::n_dofs
static unsigned int n_dofs(const unsigned int dim, const FEType &fe_t, const ElemType t)
Definition: fe_interface.C:454
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29
libMesh::FEInterface::shape
static Real shape(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int i, const Point &p)
Definition: fe_interface.C:657
libMesh::FEInterface::inverse_map
static Point inverse_map(const unsigned int dim, const FEType &fe_t, const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: fe_interface.C:590
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::NodeConstraintRow
std::map< const Node *, Real, std::less< const Node * >, Threads::scalable_allocator< std::pair< const Node *const, Real > > > NodeConstraintRow
Definition: dof_map.h:145
libMesh::remote_elem
const RemoteElem * remote_elem
Definition: remote_elem.C:57

◆ compute_node_indices()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::compute_node_indices ( const ElemType  inf_elem_type,
const unsigned int  outer_node_index,
unsigned int &  base_node,
unsigned int &  radial_node 
)
staticprotected

Computes the indices in the base base_node and in radial direction radial_node (either 0 or 1) associated to the node outer_node_index of an infinite element of type inf_elem_type.

Definition at line 361 of file inf_fe_static.C.

References libMesh::INFEDGE2, libMesh::INFHEX16, libMesh::INFHEX18, libMesh::INFHEX8, libMesh::INFPRISM12, libMesh::INFPRISM6, libMesh::INFQUAD4, and libMesh::INFQUAD6.

365 {
366  switch (inf_elem_type)
367  {
368  case INFEDGE2:
369  {
370  libmesh_assert_less (outer_node_index, 2);
371  base_node = 0;
372  radial_node = outer_node_index;
373  return;
374  }
375 
376 
377  // linear base approximation, easy to determine
378  case INFQUAD4:
379  {
380  libmesh_assert_less (outer_node_index, 4);
381  base_node = outer_node_index % 2;
382  radial_node = outer_node_index / 2;
383  return;
384  }
385 
386  case INFPRISM6:
387  {
388  libmesh_assert_less (outer_node_index, 6);
389  base_node = outer_node_index % 3;
390  radial_node = outer_node_index / 3;
391  return;
392  }
393 
394  case INFHEX8:
395  {
396  libmesh_assert_less (outer_node_index, 8);
397  base_node = outer_node_index % 4;
398  radial_node = outer_node_index / 4;
399  return;
400  }
401 
402 
403  // higher order base approximation, more work necessary
404  case INFQUAD6:
405  {
406  switch (outer_node_index)
407  {
408  case 0:
409  case 1:
410  {
411  radial_node = 0;
412  base_node = outer_node_index;
413  return;
414  }
415 
416  case 2:
417  case 3:
418  {
419  radial_node = 1;
420  base_node = outer_node_index-2;
421  return;
422  }
423 
424  case 4:
425  {
426  radial_node = 0;
427  base_node = 2;
428  return;
429  }
430 
431  case 5:
432  {
433  radial_node = 1;
434  base_node = 2;
435  return;
436  }
437 
438  default:
439  libmesh_error_msg("Unrecognized outer_node_index = " << outer_node_index);
440  }
441  }
442 
443 
444  case INFHEX16:
445  case INFHEX18:
446  {
447  switch (outer_node_index)
448  {
449  case 0:
450  case 1:
451  case 2:
452  case 3:
453  {
454  radial_node = 0;
455  base_node = outer_node_index;
456  return;
457  }
458 
459  case 4:
460  case 5:
461  case 6:
462  case 7:
463  {
464  radial_node = 1;
465  base_node = outer_node_index-4;
466  return;
467  }
468 
469  case 8:
470  case 9:
471  case 10:
472  case 11:
473  {
474  radial_node = 0;
475  base_node = outer_node_index-4;
476  return;
477  }
478 
479  case 12:
480  case 13:
481  case 14:
482  case 15:
483  {
484  radial_node = 1;
485  base_node = outer_node_index-8;
486  return;
487  }
488 
489  case 16:
490  {
491  libmesh_assert_equal_to (inf_elem_type, INFHEX18);
492  radial_node = 0;
493  base_node = 8;
494  return;
495  }
496 
497  case 17:
498  {
499  libmesh_assert_equal_to (inf_elem_type, INFHEX18);
500  radial_node = 1;
501  base_node = 8;
502  return;
503  }
504 
505  default:
506  libmesh_error_msg("Unrecognized outer_node_index = " << outer_node_index);
507  }
508  }
509 
510 
511  case INFPRISM12:
512  {
513  switch (outer_node_index)
514  {
515  case 0:
516  case 1:
517  case 2:
518  {
519  radial_node = 0;
520  base_node = outer_node_index;
521  return;
522  }
523 
524  case 3:
525  case 4:
526  case 5:
527  {
528  radial_node = 1;
529  base_node = outer_node_index-3;
530  return;
531  }
532 
533  case 6:
534  case 7:
535  case 8:
536  {
537  radial_node = 0;
538  base_node = outer_node_index-3;
539  return;
540  }
541 
542  case 9:
543  case 10:
544  case 11:
545  {
546  radial_node = 1;
547  base_node = outer_node_index-6;
548  return;
549  }
550 
551  default:
552  libmesh_error_msg("Unrecognized outer_node_index = " << outer_node_index);
553  }
554  }
555 
556 
557  default:
558  libmesh_error_msg("ERROR: Bad infinite element type=" << inf_elem_type << ", node=" << outer_node_index);
559  }
560 }

◆ compute_node_indices_fast()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::compute_node_indices_fast ( const ElemType  inf_elem_type,
const unsigned int  outer_node_index,
unsigned int &  base_node,
unsigned int &  radial_node 
)
staticprotected

Does the same as compute_node_indices(), but stores the maps for the current element type. Provided the infinite element type changes seldom, this is probably faster than using compute_node_indices () alone. This is possible since the number of nodes is not likely to change.

Definition at line 568 of file inf_fe_static.C.

References libMesh::INFEDGE2, libMesh::INFHEX16, libMesh::INFHEX18, libMesh::INFHEX8, libMesh::INFPRISM12, libMesh::INFPRISM6, libMesh::INFQUAD4, libMesh::INFQUAD6, libMesh::INVALID_ELEM, libMesh::invalid_uint, and n_nodes.

572 {
573  libmesh_assert_not_equal_to (inf_elem_type, INVALID_ELEM);
574 
575  static std::vector<unsigned int> _static_base_node_index;
576  static std::vector<unsigned int> _static_radial_node_index;
577 
578  /*
579  * fast counterpart to compute_node_indices(), uses local static buffers
580  * to store the index maps. The class member
581  * \p _compute_node_indices_fast_current_elem_type remembers
582  * the current element type.
583  *
584  * Note that there exist non-static members storing the
585  * same data. However, you never know what element type
586  * is currently used by the \p InfFE object, and what
587  * request is currently directed to the static \p InfFE
588  * members (which use \p compute_node_indices_fast()).
589  * So separate these.
590  *
591  * check whether the work for this elemtype has already
592  * been done. If so, use this index. Otherwise, refresh
593  * the buffer to this element type.
594  */
595  if (inf_elem_type==_compute_node_indices_fast_current_elem_type)
596  {
597  base_node = _static_base_node_index [outer_node_index];
598  radial_node = _static_radial_node_index[outer_node_index];
599  return;
600  }
601  else
602  {
603  // store the map for _all_ nodes for this element type
604  _compute_node_indices_fast_current_elem_type = inf_elem_type;
605 
606  unsigned int n_nodes = libMesh::invalid_uint;
607 
608  switch (inf_elem_type)
609  {
610  case INFEDGE2:
611  {
612  n_nodes = 2;
613  break;
614  }
615  case INFQUAD4:
616  {
617  n_nodes = 4;
618  break;
619  }
620  case INFQUAD6:
621  {
622  n_nodes = 6;
623  break;
624  }
625  case INFHEX8:
626  {
627  n_nodes = 8;
628  break;
629  }
630  case INFHEX16:
631  {
632  n_nodes = 16;
633  break;
634  }
635  case INFHEX18:
636  {
637  n_nodes = 18;
638  break;
639  }
640  case INFPRISM6:
641  {
642  n_nodes = 6;
643  break;
644  }
645  case INFPRISM12:
646  {
647  n_nodes = 12;
648  break;
649  }
650  default:
651  libmesh_error_msg("ERROR: Bad infinite element type=" << inf_elem_type << ", node=" << outer_node_index);
652  }
653 
654 
655  _static_base_node_index.resize (n_nodes);
656  _static_radial_node_index.resize(n_nodes);
657 
658  for (unsigned int n=0; n<n_nodes; n++)
659  compute_node_indices (inf_elem_type,
660  n,
661  _static_base_node_index [outer_node_index],
662  _static_radial_node_index[outer_node_index]);
663 
664  // and return for the specified node
665  base_node = _static_base_node_index [outer_node_index];
666  radial_node = _static_radial_node_index[outer_node_index];
667  return;
668  }
669 }
libMesh::invalid_uint
const unsigned int invalid_uint
Definition: libmesh.h:245
libMesh::InfFE::compute_node_indices
static void compute_node_indices(const ElemType inf_elem_type, const unsigned int outer_node_index, unsigned int &base_node, unsigned int &radial_node)
Definition: inf_fe_static.C:361
n_nodes
const dof_id_type n_nodes
Definition: tecplot_io.C:68
libMesh::InfFE::_compute_node_indices_fast_current_elem_type
static ElemType _compute_node_indices_fast_current_elem_type
Definition: inf_fe.h:799

◆ compute_periodic_constraints()

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::compute_periodic_constraints ( DofConstraints &  constraints,
DofMap &  dof_map,
const PeriodicBoundaries &  boundaries,
const MeshBase &  mesh,
const PointLocatorBase *  point_locator,
const unsigned int  variable_number,
const Elem *  elem 
)
staticinherited

Computes the constraint matrix contributions (for meshes with periodic boundary conditions) corresponding to variable number var_number, using generic projections.

Definition at line 1650 of file fe_base.C.

Referenced by libMesh::FEInterface::compute_periodic_constraints().

1657 {
1658  // Only bother if we truly have periodic boundaries
1659  if (boundaries.empty())
1660  return;
1661 
1662  libmesh_assert(elem);
1663 
1664  // Only constrain active elements with this method
1665  if (!elem->active())
1666  return;
1667 
1668  const unsigned int Dim = elem->dim();
1669 
1670  // We need sys_number and variable_number for DofObject methods
1671  // later
1672  const unsigned int sys_number = dof_map.sys_number();
1673 
1674  const FEType & base_fe_type = dof_map.variable_type(variable_number);
1675 
1676  // Construct FE objects for this element and its pseudo-neighbors.
1677  std::unique_ptr<FEGenericBase<OutputShape>> my_fe
1678  (FEGenericBase<OutputShape>::build(Dim, base_fe_type));
1679  const FEContinuity cont = my_fe->get_continuity();
1680 
1681  // We don't need to constrain discontinuous elements
1682  if (cont == DISCONTINUOUS)
1683  return;
1684  libmesh_assert (cont == C_ZERO || cont == C_ONE);
1685 
1686  // We'll use element size to generate relative tolerances later
1687  const Real primary_hmin = elem->hmin();
1688 
1689  std::unique_ptr<FEGenericBase<OutputShape>> neigh_fe
1690  (FEGenericBase<OutputShape>::build(Dim, base_fe_type));
1691 
1692  QGauss my_qface(Dim-1, base_fe_type.default_quadrature_order());
1693  my_fe->attach_quadrature_rule (&my_qface);
1694  std::vector<Point> neigh_qface;
1695 
1696  const std::vector<Real> & JxW = my_fe->get_JxW();
1697  const std::vector<Point> & q_point = my_fe->get_xyz();
1698  const std::vector<std::vector<OutputShape>> & phi = my_fe->get_phi();
1699  const std::vector<std::vector<OutputShape>> & neigh_phi =
1700  neigh_fe->get_phi();
1701  const std::vector<Point> * face_normals = nullptr;
1702  const std::vector<std::vector<OutputGradient>> * dphi = nullptr;
1703  const std::vector<std::vector<OutputGradient>> * neigh_dphi = nullptr;
1704  std::vector<dof_id_type> my_dof_indices, neigh_dof_indices;
1705  std::vector<unsigned int> my_side_dofs, neigh_side_dofs;
1706 
1707  if (cont != C_ZERO)
1708  {
1709  const std::vector<Point> & ref_face_normals =
1710  my_fe->get_normals();
1711  face_normals = &ref_face_normals;
1712  const std::vector<std::vector<OutputGradient>> & ref_dphi =
1713  my_fe->get_dphi();
1714  dphi = &ref_dphi;
1715  const std::vector<std::vector<OutputGradient>> & ref_neigh_dphi =
1716  neigh_fe->get_dphi();
1717  neigh_dphi = &ref_neigh_dphi;
1718  }
1719 
1720  DenseMatrix<Real> Ke;
1721  DenseVector<Real> Fe;
1722  std::vector<DenseVector<Real>> Ue;
1723 
1724  // Container to catch the boundary ids that BoundaryInfo hands us.
1725  std::vector<boundary_id_type> bc_ids;
1726 
1727  // Look at the element faces. Check to see if we need to
1728  // build constraints.
1729  const unsigned short int max_ns = elem->n_sides();
1730  for (unsigned short int s = 0; s != max_ns; ++s)
1731  {
1732  if (elem->neighbor_ptr(s))
1733  continue;
1734 
1735  mesh.get_boundary_info().boundary_ids (elem, s, bc_ids);
1736 
1737  for (const auto & boundary_id : bc_ids)
1738  {
1739  const PeriodicBoundaryBase * periodic = boundaries.boundary(boundary_id);
1740  if (periodic && periodic->is_my_variable(variable_number))
1741  {
1742  libmesh_assert(point_locator);
1743 
1744  // Get pointers to the element's neighbor.
1745  const Elem * neigh = boundaries.neighbor(boundary_id, *point_locator, elem, s);
1746 
1747  if (neigh == nullptr)
1748  libmesh_error_msg("PeriodicBoundaries point locator object returned nullptr!");
1749 
1750  // periodic (and possibly h refinement) constraints:
1751  // constrain dofs shared between
1752  // this element and ones as coarse
1753  // as or coarser than this element.
1754  if (neigh->level() <= elem->level())
1755  {
1756  unsigned int s_neigh =
1757  mesh.get_boundary_info().side_with_boundary_id(neigh, periodic->pairedboundary);
1758  libmesh_assert_not_equal_to (s_neigh, libMesh::invalid_uint);
1759 
1760 #ifdef LIBMESH_ENABLE_AMR
1761  // Find the minimum p level; we build the h constraint
1762  // matrix with this and then constrain away all higher p
1763  // DoFs.
1764  libmesh_assert(neigh->active());
1765  const unsigned int min_p_level =
1766  std::min(elem->p_level(), neigh->p_level());
1767 
1768  // we may need to make the FE objects reinit with the
1769  // minimum shared p_level
1770  // FIXME - I hate using const_cast<> and avoiding
1771  // accessor functions; there's got to be a
1772  // better way to do this!
1773  const unsigned int old_elem_level = elem->p_level();
1774  if (old_elem_level != min_p_level)
1775  (const_cast<Elem *>(elem))->hack_p_level(min_p_level);
1776  const unsigned int old_neigh_level = neigh->p_level();
1777  if (old_neigh_level != min_p_level)
1778  (const_cast<Elem *>(neigh))->hack_p_level(min_p_level);
1779 #endif // #ifdef LIBMESH_ENABLE_AMR
1780 
1781  // We can do a projection with a single integration,
1782  // due to the assumption of nested finite element
1783  // subspaces.
1784  // FIXME: it might be more efficient to do nodes,
1785  // then edges, then side, to reduce the size of the
1786  // Cholesky factorization(s)
1787  my_fe->reinit(elem, s);
1788 
1789  dof_map.dof_indices (elem, my_dof_indices,
1790  variable_number);
1791  dof_map.dof_indices (neigh, neigh_dof_indices,
1792  variable_number);
1793 
1794  // We use neigh_dof_indices_all_variables in the case that the
1795  // periodic boundary condition involves mappings between multiple
1796  // variables.
1797  std::vector<std::vector<dof_id_type>> neigh_dof_indices_all_variables;
1798  if(periodic->has_transformation_matrix())
1799  {
1800  const std::set<unsigned int> & variables = periodic->get_variables();
1801  neigh_dof_indices_all_variables.resize(variables.size());
1802  unsigned int index = 0;
1803  for(unsigned int var : variables)
1804  {
1805  dof_map.dof_indices (neigh, neigh_dof_indices_all_variables[index],
1806  var);
1807  index++;
1808  }
1809  }
1810 
1811  const unsigned int n_qp = my_qface.n_points();
1812 
1813  // Translate the quadrature points over to the
1814  // neighbor's boundary
1815  std::vector<Point> neigh_point(q_point.size());
1816  for (auto i : index_range(neigh_point))
1817  neigh_point[i] = periodic->get_corresponding_pos(q_point[i]);
1818 
1819  FEInterface::inverse_map (Dim, base_fe_type, neigh,
1820  neigh_point, neigh_qface);
1821 
1822  neigh_fe->reinit(neigh, &neigh_qface);
1823 
1824  // We're only concerned with DOFs whose values (and/or first
1825  // derivatives for C1 elements) are supported on side nodes
1826  FEInterface::dofs_on_side(elem, Dim, base_fe_type, s, my_side_dofs);
1827  FEInterface::dofs_on_side(neigh, Dim, base_fe_type, s_neigh, neigh_side_dofs);
1828 
1829  // We're done with functions that examine Elem::p_level(),
1830  // so let's unhack those levels
1831 #ifdef LIBMESH_ENABLE_AMR
1832  if (elem->p_level() != old_elem_level)
1833  (const_cast<Elem *>(elem))->hack_p_level(old_elem_level);
1834  if (neigh->p_level() != old_neigh_level)
1835  (const_cast<Elem *>(neigh))->hack_p_level(old_neigh_level);
1836 #endif // #ifdef LIBMESH_ENABLE_AMR
1837 
1838  const unsigned int n_side_dofs =
1839  cast_int<unsigned int>
1840  (my_side_dofs.size());
1841  libmesh_assert_equal_to (n_side_dofs, neigh_side_dofs.size());
1842 
1843  Ke.resize (n_side_dofs, n_side_dofs);
1844  Ue.resize(n_side_dofs);
1845 
1846  // Form the projection matrix, (inner product of fine basis
1847  // functions against fine test functions)
1848  for (unsigned int is = 0; is != n_side_dofs; ++is)
1849  {
1850  const unsigned int i = my_side_dofs[is];
1851  for (unsigned int js = 0; js != n_side_dofs; ++js)
1852  {
1853  const unsigned int j = my_side_dofs[js];
1854  for (unsigned int qp = 0; qp != n_qp; ++qp)
1855  {
1856  Ke(is,js) += JxW[qp] *
1857  TensorTools::inner_product(phi[i][qp],
1858  phi[j][qp]);
1859  if (cont != C_ZERO)
1860  Ke(is,js) += JxW[qp] *
1861  TensorTools::inner_product((*dphi)[i][qp] *
1862  (*face_normals)[qp],
1863  (*dphi)[j][qp] *
1864  (*face_normals)[qp]);
1865  }
1866  }
1867  }
1868 
1869  // Form the right hand sides, (inner product of coarse basis
1870  // functions against fine test functions)
1871  for (unsigned int is = 0; is != n_side_dofs; ++is)
1872  {
1873  const unsigned int i = neigh_side_dofs[is];
1874  Fe.resize (n_side_dofs);
1875  for (unsigned int js = 0; js != n_side_dofs; ++js)
1876  {
1877  const unsigned int j = my_side_dofs[js];
1878  for (unsigned int qp = 0; qp != n_qp; ++qp)
1879  {
1880  Fe(js) += JxW[qp] *
1881  TensorTools::inner_product(neigh_phi[i][qp],
1882  phi[j][qp]);
1883  if (cont != C_ZERO)
1884  Fe(js) += JxW[qp] *
1885  TensorTools::inner_product((*neigh_dphi)[i][qp] *
1886  (*face_normals)[qp],
1887  (*dphi)[j][qp] *
1888  (*face_normals)[qp]);
1889  }
1890  }
1891  Ke.cholesky_solve(Fe, Ue[is]);
1892  }
1893 
1894  // Make sure we're not adding recursive constraints
1895  // due to the redundancy in the way we add periodic
1896  // boundary constraints
1897  //
1898  // In order for this to work while threaded or on
1899  // distributed meshes, we need a rigorous way to
1900  // avoid recursive constraints. Here it is:
1901  //
1902  // For vertex DoFs, if there is a "prior" element
1903  // (i.e. a coarser element or an equally refined
1904  // element with a lower id) on this boundary which
1905  // contains the vertex point, then we will avoid
1906  // generating constraints; the prior element (or
1907  // something prior to it) may do so. If we are the
1908  // most prior (or "primary") element on this
1909  // boundary sharing this point, then we look at the
1910  // boundary periodic to us, we find the primary
1911  // element there, and if that primary is coarser or
1912  // equal-but-lower-id, then our vertex dofs are
1913  // constrained in terms of that element.
1914  //
1915  // For edge DoFs, if there is a coarser element
1916  // on this boundary sharing this edge, then we will
1917  // avoid generating constraints (we will be
1918  // constrained indirectly via AMR constraints
1919  // connecting us to the coarser element's DoFs). If
1920  // we are the coarsest element sharing this edge,
1921  // then we generate constraints if and only if we
1922  // are finer than the coarsest element on the
1923  // boundary periodic to us sharing the corresponding
1924  // periodic edge, or if we are at equal level but
1925  // our edge nodes have higher ids than the periodic
1926  // edge nodes (sorted from highest to lowest, then
1927  // compared lexicographically)
1928  //
1929  // For face DoFs, we generate constraints if we are
1930  // finer than our periodic neighbor, or if we are at
1931  // equal level but our element id is higher than its
1932  // element id.
1933  //
1934  // If the primary neighbor is also the current elem
1935  // (a 1-element-thick mesh) then we choose which
1936  // vertex dofs to constrain via lexicographic
1937  // ordering on point locations
1938 
1939  // FIXME: This code doesn't yet properly handle
1940  // cases where multiple different periodic BCs
1941  // intersect.
1942  std::set<dof_id_type> my_constrained_dofs;
1943 
1944  // Container to catch boundary IDs handed back by BoundaryInfo.
1945  std::vector<boundary_id_type> new_bc_ids;
1946 
1947  for (unsigned int n = 0; n != elem->n_nodes(); ++n)
1948  {
1949  if (!elem->is_node_on_side(n,s))
1950  continue;
1951 
1952  const Node & my_node = elem->node_ref(n);
1953 
1954  if (elem->is_vertex(n))
1955  {
1956  // Find all boundary ids that include this
1957  // point and have periodic boundary
1958  // conditions for this variable
1959  std::set<boundary_id_type> point_bcids;
1960 
1961  for (unsigned int new_s = 0;
1962  new_s != max_ns; ++new_s)
1963  {
1964  if (!elem->is_node_on_side(n,new_s))
1965  continue;
1966 
1967  mesh.get_boundary_info().boundary_ids (elem, s, new_bc_ids);
1968 
1969  for (const auto & new_boundary_id : new_bc_ids)
1970  {
1971  const PeriodicBoundaryBase * new_periodic = boundaries.boundary(new_boundary_id);
1972  if (new_periodic && new_periodic->is_my_variable(variable_number))
1973  point_bcids.insert(new_boundary_id);
1974  }
1975  }
1976 
1977  // See if this vertex has point neighbors to
1978  // defer to
1979  if (primary_boundary_point_neighbor
1980  (elem, my_node, mesh.get_boundary_info(), point_bcids)
1981  != elem)
1982  continue;
1983 
1984  // Find the complementary boundary id set
1985  std::set<boundary_id_type> point_pairedids;
1986  for (const auto & new_boundary_id : point_bcids)
1987  {
1988  const PeriodicBoundaryBase * new_periodic = boundaries.boundary(new_boundary_id);
1989  point_pairedids.insert(new_periodic->pairedboundary);
1990  }
1991 
1992  // What do we want to constrain against?
1993  const Elem * primary_elem = nullptr;
1994  const Elem * main_neigh = nullptr;
1995  Point main_pt = my_node,
1996  primary_pt = my_node;
1997 
1998  for (const auto & new_boundary_id : point_bcids)
1999  {
2000  // Find the corresponding periodic point and
2001  // its primary neighbor
2002  const PeriodicBoundaryBase * new_periodic = boundaries.boundary(new_boundary_id);
2003 
2004  const Point neigh_pt =
2005  new_periodic->get_corresponding_pos(my_node);
2006 
2007  // If the point is getting constrained
2008  // to itself by this PBC then we don't
2009  // generate any constraints
2010  if (neigh_pt.absolute_fuzzy_equals
2011  (my_node, primary_hmin*TOLERANCE))
2012  continue;
2013 
2014  // Otherwise we'll have a constraint in
2015  // one direction or another
2016  if (!primary_elem)
2017  primary_elem = elem;
2018 
2019  const Elem * primary_neigh =
2020  primary_boundary_point_neighbor(neigh, neigh_pt,
2021  mesh.get_boundary_info(),
2022  point_pairedids);
2023 
2024  libmesh_assert(primary_neigh);
2025 
2026  if (new_boundary_id == boundary_id)
2027  {
2028  main_neigh = primary_neigh;
2029  main_pt = neigh_pt;
2030  }
2031 
2032  // Finer elements will get constrained in
2033  // terms of coarser neighbors, not the
2034  // other way around
2035  if ((primary_neigh->level() > primary_elem->level()) ||
2036 
2037  // For equal-level elements, the one with
2038  // higher id gets constrained in terms of
2039  // the one with lower id
2040  (primary_neigh->level() == primary_elem->level() &&
2041  primary_neigh->id() > primary_elem->id()) ||
2042 
2043  // On a one-element-thick mesh, we compare
2044  // points to see what side gets constrained
2045  (primary_neigh == primary_elem &&
2046  (neigh_pt > primary_pt)))
2047  continue;
2048 
2049  primary_elem = primary_neigh;
2050  primary_pt = neigh_pt;
2051  }
2052 
2053  if (!primary_elem ||
2054  primary_elem != main_neigh ||
2055  primary_pt != main_pt)
2056  continue;
2057  }
2058  else if (elem->is_edge(n))
2059  {
2060  // Find which edge we're on
2061  unsigned int e=0;
2062  for (; e != elem->n_edges(); ++e)
2063  {
2064  if (elem->is_node_on_edge(n,e))
2065  break;
2066  }
2067  libmesh_assert_less (e, elem->n_edges());
2068 
2069  // Find the edge end nodes
2070  const Node
2071  * e1 = nullptr,
2072  * e2 = nullptr;
2073  for (unsigned int nn = 0; nn != elem->n_nodes(); ++nn)
2074  {
2075  if (nn == n)
2076  continue;
2077 
2078  if (elem->is_node_on_edge(nn, e))
2079  {
2080  if (e1 == nullptr)
2081  {
2082  e1 = elem->node_ptr(nn);
2083  }
2084  else
2085  {
2086  e2 = elem->node_ptr(nn);
2087  break;
2088  }
2089  }
2090  }
2091  libmesh_assert (e1 && e2);
2092 
2093  // Find all boundary ids that include this
2094  // edge and have periodic boundary
2095  // conditions for this variable
2096  std::set<boundary_id_type> edge_bcids;
2097 
2098  for (unsigned int new_s = 0;
2099  new_s != max_ns; ++new_s)
2100  {
2101  if (!elem->is_node_on_side(n,new_s))
2102  continue;
2103 
2104  // We're reusing the new_bc_ids vector created outside the loop over nodes.
2105  mesh.get_boundary_info().boundary_ids (elem, s, new_bc_ids);
2106 
2107  for (const auto & new_boundary_id : new_bc_ids)
2108  {
2109  const PeriodicBoundaryBase * new_periodic = boundaries.boundary(new_boundary_id);
2110  if (new_periodic && new_periodic->is_my_variable(variable_number))
2111  edge_bcids.insert(new_boundary_id);
2112  }
2113  }
2114 
2115 
2116  // See if this edge has neighbors to defer to
2117  if (primary_boundary_edge_neighbor
2118  (elem, *e1, *e2, mesh.get_boundary_info(), edge_bcids)
2119  != elem)
2120  continue;
2121 
2122  // Find the complementary boundary id set
2123  std::set<boundary_id_type> edge_pairedids;
2124  for (const auto & new_boundary_id : edge_bcids)
2125  {
2126  const PeriodicBoundaryBase * new_periodic = boundaries.boundary(new_boundary_id);
2127  edge_pairedids.insert(new_periodic->pairedboundary);
2128  }
2129 
2130  // What do we want to constrain against?
2131  const Elem * primary_elem = nullptr;
2132  const Elem * main_neigh = nullptr;
2133  Point main_pt1 = *e1,
2134  main_pt2 = *e2,
2135  primary_pt1 = *e1,
2136  primary_pt2 = *e2;
2137 
2138  for (const auto & new_boundary_id : edge_bcids)
2139  {
2140  // Find the corresponding periodic edge and
2141  // its primary neighbor
2142  const PeriodicBoundaryBase * new_periodic = boundaries.boundary(new_boundary_id);
2143 
2144  Point neigh_pt1 = new_periodic->get_corresponding_pos(*e1),
2145  neigh_pt2 = new_periodic->get_corresponding_pos(*e2);
2146 
2147  // If the edge is getting constrained
2148  // to itself by this PBC then we don't
2149  // generate any constraints
2150  if (neigh_pt1.absolute_fuzzy_equals
2151  (*e1, primary_hmin*TOLERANCE) &&
2152  neigh_pt2.absolute_fuzzy_equals
2153  (*e2, primary_hmin*TOLERANCE))
2154  continue;
2155 
2156  // Otherwise we'll have a constraint in
2157  // one direction or another
2158  if (!primary_elem)
2159  primary_elem = elem;
2160 
2161  const Elem * primary_neigh = primary_boundary_edge_neighbor
2162  (neigh, neigh_pt1, neigh_pt2,
2163  mesh.get_boundary_info(), edge_pairedids);
2164 
2165  libmesh_assert(primary_neigh);
2166 
2167  if (new_boundary_id == boundary_id)
2168  {
2169  main_neigh = primary_neigh;
2170  main_pt1 = neigh_pt1;
2171  main_pt2 = neigh_pt2;
2172  }
2173 
2174  // If we have a one-element thick mesh,
2175  // we'll need to sort our points to get a
2176  // consistent ordering rule
2177  //
2178  // Use >= in this test to make sure that,
2179  // for angular constraints, no node gets
2180  // constrained to itself.
2181  if (primary_neigh == primary_elem)
2182  {
2183  if (primary_pt1 > primary_pt2)
2184  std::swap(primary_pt1, primary_pt2);
2185  if (neigh_pt1 > neigh_pt2)
2186  std::swap(neigh_pt1, neigh_pt2);
2187 
2188  if (neigh_pt2 >= primary_pt2)
2189  continue;
2190  }
2191 
2192  // Otherwise:
2193  // Finer elements will get constrained in
2194  // terms of coarser ones, not the other way
2195  // around
2196  if ((primary_neigh->level() > primary_elem->level()) ||
2197 
2198  // For equal-level elements, the one with
2199  // higher id gets constrained in terms of
2200  // the one with lower id
2201  (primary_neigh->level() == primary_elem->level() &&
2202  primary_neigh->id() > primary_elem->id()))
2203  continue;
2204 
2205  primary_elem = primary_neigh;
2206  primary_pt1 = neigh_pt1;
2207  primary_pt2 = neigh_pt2;
2208  }
2209 
2210  if (!primary_elem ||
2211  primary_elem != main_neigh ||
2212  primary_pt1 != main_pt1 ||
2213  primary_pt2 != main_pt2)
2214  continue;
2215  }
2216  else if (elem->is_face(n))
2217  {
2218  // If we have a one-element thick mesh,
2219  // use the ordering of the face node and its
2220  // periodic counterpart to determine what
2221  // gets constrained
2222  if (neigh == elem)
2223  {
2224  const Point neigh_pt =
2225  periodic->get_corresponding_pos(my_node);
2226  if (neigh_pt > my_node)
2227  continue;
2228  }
2229 
2230  // Otherwise:
2231  // Finer elements will get constrained in
2232  // terms of coarser ones, not the other way
2233  // around
2234  if ((neigh->level() > elem->level()) ||
2235 
2236  // For equal-level elements, the one with
2237  // higher id gets constrained in terms of
2238  // the one with lower id
2239  (neigh->level() == elem->level() &&
2240  neigh->id() > elem->id()))
2241  continue;
2242  }
2243 
2244  // If we made it here without hitting a continue
2245  // statement, then we're at a node whose dofs
2246  // should be constrained by this element's
2247  // calculations.
2248  const unsigned int n_comp =
2249  my_node.n_comp(sys_number, variable_number);
2250 
2251  for (unsigned int i=0; i != n_comp; ++i)
2252  my_constrained_dofs.insert
2253  (my_node.dof_number
2254  (sys_number, variable_number, i));
2255  }
2256 
2257  // FIXME: old code for disambiguating periodic BCs:
2258  // this is not threadsafe nor safe to run on a
2259  // non-serialized mesh.
2260  /*
2261  std::vector<bool> recursive_constraint(n_side_dofs, false);
2262 
2263  for (unsigned int is = 0; is != n_side_dofs; ++is)
2264  {
2265  const unsigned int i = neigh_side_dofs[is];
2266  const dof_id_type their_dof_g = neigh_dof_indices[i];
2267  libmesh_assert_not_equal_to (their_dof_g, DofObject::invalid_id);
2268 
2269  {
2270  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
2271 
2272  if (!dof_map.is_constrained_dof(their_dof_g))
2273  continue;
2274  }
2275 
2276  DofConstraintRow & their_constraint_row =
2277  constraints[their_dof_g].first;
2278 
2279  for (unsigned int js = 0; js != n_side_dofs; ++js)
2280  {
2281  const unsigned int j = my_side_dofs[js];
2282  const dof_id_type my_dof_g = my_dof_indices[j];
2283  libmesh_assert_not_equal_to (my_dof_g, DofObject::invalid_id);
2284 
2285  if (their_constraint_row.count(my_dof_g))
2286  recursive_constraint[js] = true;
2287  }
2288  }
2289  */
2290 
2291  for (unsigned int js = 0; js != n_side_dofs; ++js)
2292  {
2293  // FIXME: old code path
2294  // if (recursive_constraint[js])
2295  // continue;
2296 
2297  const unsigned int j = my_side_dofs[js];
2298  const dof_id_type my_dof_g = my_dof_indices[j];
2299  libmesh_assert_not_equal_to (my_dof_g, DofObject::invalid_id);
2300 
2301  // FIXME: new code path
2302  if (!my_constrained_dofs.count(my_dof_g))
2303  continue;
2304 
2305  DofConstraintRow * constraint_row;
2306 
2307  // we may be running constraint methods concurrently
2308  // on multiple threads, so we need a lock to
2309  // ensure that this constraint is "ours"
2310  {
2311  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
2312 
2313  if (dof_map.is_constrained_dof(my_dof_g))
2314  continue;
2315 
2316  constraint_row = &(constraints[my_dof_g]);
2317  libmesh_assert(constraint_row->empty());
2318  }
2319 
2320  for (unsigned int is = 0; is != n_side_dofs; ++is)
2321  {
2322  const unsigned int i = neigh_side_dofs[is];
2323  const dof_id_type their_dof_g = neigh_dof_indices[i];
2324  libmesh_assert_not_equal_to (their_dof_g, DofObject::invalid_id);
2325 
2326  // Periodic constraints should never be
2327  // self-constraints
2328  // libmesh_assert_not_equal_to (their_dof_g, my_dof_g);
2329 
2330  const Real their_dof_value = Ue[is](js);
2331 
2332  if (their_dof_g == my_dof_g)
2333  {
2334  libmesh_assert_less (std::abs(their_dof_value-1.), 1.e-5);
2335  for (unsigned int k = 0; k != n_side_dofs; ++k)
2336  libmesh_assert(k == is || std::abs(Ue[k](js)) < 1.e-5);
2337  continue;
2338  }
2339 
2340  if (std::abs(their_dof_value) < 10*TOLERANCE)
2341  continue;
2342 
2343  if(!periodic->has_transformation_matrix())
2344  {
2345  constraint_row->insert(std::make_pair(their_dof_g,
2346  their_dof_value));
2347  }
2348  else
2349  {
2350  // In this case the current variable is constrained in terms of other variables.
2351  // We assume that all variables in this constraint have the same FE type (this
2352  // is asserted below), and hence we can create the constraint row contribution
2353  // by multiplying their_dof_value by the corresponding row of the transformation
2354  // matrix.
2355 
2356  const std::set<unsigned int> & variables = periodic->get_variables();
2357  neigh_dof_indices_all_variables.resize(variables.size());
2358  unsigned int index = 0;
2359  for(unsigned int other_var : variables)
2360  {
2361  libmesh_assert_msg(base_fe_type == dof_map.variable_type(other_var), "FE types must match for all variables involved in constraint");
2362 
2363  Real var_weighting = periodic->get_transformation_matrix()(variable_number, other_var);
2364  constraint_row->insert(std::make_pair(neigh_dof_indices_all_variables[index][i],
2365  var_weighting*their_dof_value));
2366  index++;
2367  }
2368  }
2369 
2370  }
2371  }
2372  }
2373  // p refinement constraints:
2374  // constrain dofs shared between
2375  // active elements and neighbors with
2376  // lower polynomial degrees
2377 #ifdef LIBMESH_ENABLE_AMR
2378  const unsigned int min_p_level =
2379  neigh->min_p_level_by_neighbor(elem, elem->p_level());
2380  if (min_p_level < elem->p_level())
2381  {
2382  // Adaptive p refinement of non-hierarchic bases will
2383  // require more coding
2384  libmesh_assert(my_fe->is_hierarchic());
2385  dof_map.constrain_p_dofs(variable_number, elem,
2386  s, min_p_level);
2387  }
2388 #endif // #ifdef LIBMESH_ENABLE_AMR
2389  }
2390  }
2391  }
2392 }
libMesh::FEType
Manages the family, order, etc. parameters for a given FE.
Definition: fe_type.h:179
std::abs
double abs(double a)
Definition: libmesh_augment_std_namespace.h:59
libMesh::DofObject::dof_number
dof_id_type dof_number(const unsigned int s, const unsigned int var, const unsigned int comp) const
Definition: dof_object.h:833
libMesh::Node
A geometric point in (x,y,z) space associated with a DOF.
Definition: node.h:52
libMesh::invalid_uint
const unsigned int invalid_uint
Definition: libmesh.h:245
libMesh::DofObject::n_comp
unsigned int n_comp(const unsigned int s, const unsigned int var) const
Definition: dof_object.h:803
libMesh::Elem::is_face
virtual bool is_face(const unsigned int i) const =0
libMesh::DofMap::dof_indices
void dof_indices(const Elem *const elem, std::vector< dof_id_type > &di) const
Definition: dof_map.C:1930
libMesh::FEInterface::dofs_on_side
static void dofs_on_side(const Elem *const elem, const unsigned int dim, const FEType &fe_t, unsigned int s, std::vector< unsigned int > &di)
Definition: fe_interface.C:523
libMesh::PeriodicBoundaryBase::get_variables
const std::set< unsigned int > & get_variables() const
Definition: periodic_boundary_base.C:106
libMesh::DenseVector::resize
void resize(const unsigned int n)
Definition: dense_vector.h:355
libMesh::DofMap::variable_type
const FEType & variable_type(const unsigned int c) const
Definition: dof_map.h:1792
libMesh::BoundaryInfo::side_with_boundary_id
unsigned int side_with_boundary_id(const Elem *const elem, const boundary_id_type boundary_id) const
Definition: boundary_info.C:1558
libMesh::Elem
The base class for all geometric element types.
Definition: elem.h:100
mesh
MeshBase & mesh
Definition: mesh_communication.C:1245
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::PeriodicBoundaries::boundary
PeriodicBoundaryBase * boundary(boundary_id_type id)
Definition: periodic_boundaries.C:40
libMesh::Elem::is_node_on_side
virtual bool is_node_on_side(const unsigned int n, const unsigned int s) const =0
libMesh::FEType::default_quadrature_order
Order default_quadrature_order() const
Definition: fe_type.h:333
libMesh::Elem::p_level
unsigned int p_level() const
Definition: elem.h:2555
libMesh::TOLERANCE
static const Real TOLERANCE
Definition: libmesh_common.h:139
libMesh::MeshBase::get_boundary_info
const BoundaryInfo & get_boundary_info() const
Definition: mesh_base.h:131
libMesh::Elem::min_p_level_by_neighbor
unsigned int min_p_level_by_neighbor(const Elem *neighbor, unsigned int current_min) const
Definition: elem.C:1870
libMesh::DofMap::sys_number
unsigned int sys_number() const
Definition: dof_map.h:1744
libMesh::BoundaryInfo::boundary_ids
std::vector< boundary_id_type > boundary_ids(const Node *node) const
Definition: boundary_info.C:948
libMesh::Elem::is_node_on_edge
virtual bool is_node_on_edge(const unsigned int n, const unsigned int e) const =0
libMesh::PeriodicBoundaryBase::get_corresponding_pos
virtual Point get_corresponding_pos(const Point &pt) const =0
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498
libMesh::Elem::node_ref
const Node & node_ref(const unsigned int i) const
Definition: elem.h:1979
libMesh::DofObject::id
dof_id_type id() const
Definition: dof_object.h:655
libMesh::Elem::hmin
virtual Real hmin() const
Definition: elem.C:356
libMesh::Elem::n_nodes
virtual unsigned int n_nodes() const =0
libMesh::DofMap::is_constrained_dof
bool is_constrained_dof(const dof_id_type dof) const
Definition: dof_map.h:1829
libMesh::DofObject::invalid_id
static const dof_id_type invalid_id
Definition: dof_object.h:347
libMesh::FEInterface::inverse_map
static Point inverse_map(const unsigned int dim, const FEType &fe_t, const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: fe_interface.C:590
libMesh::Elem::n_edges
virtual unsigned int n_edges() const =0
libMesh::TypeVector::absolute_fuzzy_equals
bool absolute_fuzzy_equals(const TypeVector< T > &rhs, Real tol=TOLERANCE) const
Definition: type_vector.h:965
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503
libMesh::PeriodicBoundaryBase::get_transformation_matrix
const DenseMatrix< Real > & get_transformation_matrix() const
Definition: periodic_boundary_base.C:81
libMesh::Elem::n_sides
virtual unsigned int n_sides() const =0
libMesh::Elem::neighbor_ptr
const Elem * neighbor_ptr(unsigned int i) const
Definition: elem.h:2050
libMesh::Elem::level
unsigned int level() const
Definition: elem.h:2521
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::PeriodicBoundaries::neighbor
const Elem * neighbor(boundary_id_type boundary_id, const PointLocatorBase &point_locator, const Elem *e, unsigned int side) const
Definition: periodic_boundaries.C:61
libMesh::Elem::dim
virtual unsigned short dim() const =0
libMesh::Elem::node_ptr
const Node * node_ptr(const unsigned int i) const
Definition: elem.h:1957
libMesh::Elem::is_vertex
virtual bool is_vertex(const unsigned int i) const =0
swap
void swap(Iterator &lhs, Iterator &rhs)
Definition: variant_filter_iterator.h:478
libMesh::PeriodicBoundaryBase::is_my_variable
bool is_my_variable(unsigned int var_num) const
Definition: periodic_boundary_base.C:66
libMesh::DofConstraintRow
std::map< dof_id_type, Real, std::less< dof_id_type >, Threads::scalable_allocator< std::pair< const dof_id_type, Real > > > DofConstraintRow
Definition: dof_map.h:97
libMesh::DenseMatrix::resize
void resize(const unsigned int new_m, const unsigned int new_n)
Definition: dense_matrix.h:792
libMesh::QGauss
Implements 1, 2, and 3D "Gaussian" quadrature rules.
Definition: quadrature_gauss.h:39
libMesh::PeriodicBoundaryBase
Base class for all PeriodicBoundary implementations.
Definition: periodic_boundary_base.h:49
libMesh::DenseMatrix::cholesky_solve
void cholesky_solve(const DenseVector< T2 > &b, DenseVector< T2 > &x)
Definition: dense_matrix_impl.h:929
libMesh::DenseMatrix
A matrix object used for finite element assembly and numerics.
Definition: dense_matrix.h:54
libMesh::Elem::active
bool active() const
Definition: elem.h:2390
std::min
long double min(long double a, double b)
Definition: libmesh_augment_std_namespace.h:29
libMesh::Point
A geometric point in (x,y,z) space.
Definition: point.h:38
libMesh::Elem::is_edge
virtual bool is_edge(const unsigned int i) const =0
libMesh::TensorTools::inner_product
boostcopy::enable_if_c< ScalarTraits< T >::value &&ScalarTraits< T2 >::value, typename CompareTypes< T, T2 >::supertype >::type inner_product(const T &a, const T2 &b)
Definition: tensor_tools.h:47
libMesh::DofMap::constrain_p_dofs
void constrain_p_dofs(unsigned int var, const Elem *elem, unsigned int s, unsigned int p)
Definition: dof_map_constraints.C:4208
libMesh::dof_id_type
uint8_t dof_id_type
Definition: id_types.h:64

◆ compute_periodic_node_constraints()

void libMesh::FEAbstract::compute_periodic_node_constraints ( NodeConstraints &  constraints,
const PeriodicBoundaries &  boundaries,
const MeshBase &  mesh,
const PointLocatorBase *  point_locator,
const Elem *  elem 
)
staticinherited

Computes the node position constraint equation contributions (for meshes with periodic boundary conditions)

Definition at line 965 of file fe_abstract.C.

References libMesh::Elem::active(), libMesh::PeriodicBoundaries::boundary(), libMesh::Elem::build_side_ptr(), libMesh::Elem::default_order(), libMesh::Elem::dim(), libMesh::FEAbstract::fe_type, libMesh::PeriodicBoundaryBase::get_corresponding_pos(), libMesh::invalid_uint, libMesh::FEInterface::inverse_map(), libMesh::LAGRANGE, libMesh::Elem::level(), mesh, libMesh::FEInterface::n_dofs(), libMesh::PeriodicBoundaries::neighbor(), libMesh::Elem::neighbor_ptr(), libMesh::PeriodicBoundaryBase::pairedboundary, libMesh::Real, libMesh::FEInterface::shape(), libMesh::Elem::side_index_range(), and libMesh::Threads::spin_mtx.

970 {
971  // Only bother if we truly have periodic boundaries
972  if (boundaries.empty())
973  return;
974 
975  libmesh_assert(elem);
976 
977  // Only constrain active elements with this method
978  if (!elem->active())
979  return;
980 
981  const unsigned int Dim = elem->dim();
982 
983  // We currently always use LAGRANGE mappings for geometry
984  const FEType fe_type(elem->default_order(), LAGRANGE);
985 
986  // Pull objects out of the loop to reduce heap operations
987  std::vector<const Node *> my_nodes, neigh_nodes;
988  std::unique_ptr<const Elem> my_side, neigh_side;
989 
990  // Look at the element faces. Check to see if we need to
991  // build constraints.
992  std::vector<boundary_id_type> bc_ids;
993  for (auto s : elem->side_index_range())
994  {
995  if (elem->neighbor_ptr(s))
996  continue;
997 
998  mesh.get_boundary_info().boundary_ids (elem, s, bc_ids);
999  for (const auto & boundary_id : bc_ids)
1000  {
1001  const PeriodicBoundaryBase * periodic = boundaries.boundary(boundary_id);
1002  if (periodic)
1003  {
1004  libmesh_assert(point_locator);
1005 
1006  // Get pointers to the element's neighbor.
1007  const Elem * neigh = boundaries.neighbor(boundary_id, *point_locator, elem, s);
1008 
1009  // h refinement constraints:
1010  // constrain dofs shared between
1011  // this element and ones as coarse
1012  // as or coarser than this element.
1013  if (neigh->level() <= elem->level())
1014  {
1015  unsigned int s_neigh =
1016  mesh.get_boundary_info().side_with_boundary_id(neigh, periodic->pairedboundary);
1017  libmesh_assert_not_equal_to (s_neigh, libMesh::invalid_uint);
1018 
1019 #ifdef LIBMESH_ENABLE_AMR
1020  libmesh_assert(neigh->active());
1021 #endif // #ifdef LIBMESH_ENABLE_AMR
1022 
1023  elem->build_side_ptr(my_side, s);
1024  neigh->build_side_ptr(neigh_side, s_neigh);
1025 
1026  const unsigned int n_side_nodes = my_side->n_nodes();
1027 
1028  my_nodes.clear();
1029  my_nodes.reserve (n_side_nodes);
1030  neigh_nodes.clear();
1031  neigh_nodes.reserve (n_side_nodes);
1032 
1033  for (unsigned int n=0; n != n_side_nodes; ++n)
1034  my_nodes.push_back(my_side->node_ptr(n));
1035 
1036  for (unsigned int n=0; n != n_side_nodes; ++n)
1037  neigh_nodes.push_back(neigh_side->node_ptr(n));
1038 
1039  // Make sure we're not adding recursive constraints
1040  // due to the redundancy in the way we add periodic
1041  // boundary constraints, or adding constraints to
1042  // nodes that already have AMR constraints
1043  std::vector<bool> skip_constraint(n_side_nodes, false);
1044 
1045  for (unsigned int my_side_n=0;
1046  my_side_n < n_side_nodes;
1047  my_side_n++)
1048  {
1049  libmesh_assert_less (my_side_n, FEInterface::n_dofs(Dim-1, fe_type, my_side->type()));
1050 
1051  const Node * my_node = my_nodes[my_side_n];
1052 
1053  // Figure out where my node lies on their reference element.
1054  const Point neigh_point = periodic->get_corresponding_pos(*my_node);
1055 
1056  const Point mapped_point = FEInterface::inverse_map(Dim-1, fe_type,
1057  neigh_side.get(),
1058  neigh_point);
1059 
1060  // If we've already got a constraint on this
1061  // node, then the periodic constraint is
1062  // redundant
1063  {
1064  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
1065 
1066  if (constraints.count(my_node))
1067  {
1068  skip_constraint[my_side_n] = true;
1069  continue;
1070  }
1071  }
1072 
1073  // Compute the neighbors's side shape function values.
1074  for (unsigned int their_side_n=0;
1075  their_side_n < n_side_nodes;
1076  their_side_n++)
1077  {
1078  libmesh_assert_less (their_side_n, FEInterface::n_dofs(Dim-1, fe_type, neigh_side->type()));
1079 
1080  const Node * their_node = neigh_nodes[their_side_n];
1081 
1082  // If there's a constraint on an opposing node,
1083  // we need to see if it's constrained by
1084  // *our side* making any periodic constraint
1085  // on us recursive
1086  {
1087  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
1088 
1089  if (!constraints.count(their_node))
1090  continue;
1091 
1092  const NodeConstraintRow & their_constraint_row =
1093  constraints[their_node].first;
1094 
1095  for (unsigned int orig_side_n=0;
1096  orig_side_n < n_side_nodes;
1097  orig_side_n++)
1098  {
1099  libmesh_assert_less (orig_side_n, FEInterface::n_dofs(Dim-1, fe_type, my_side->type()));
1100 
1101  const Node * orig_node = my_nodes[orig_side_n];
1102 
1103  if (their_constraint_row.count(orig_node))
1104  skip_constraint[orig_side_n] = true;
1105  }
1106  }
1107  }
1108  }
1109  for (unsigned int my_side_n=0;
1110  my_side_n < n_side_nodes;
1111  my_side_n++)
1112  {
1113  libmesh_assert_less (my_side_n, FEInterface::n_dofs(Dim-1, fe_type, my_side->type()));
1114 
1115  if (skip_constraint[my_side_n])
1116  continue;
1117 
1118  const Node * my_node = my_nodes[my_side_n];
1119 
1120  // Figure out where my node lies on their reference element.
1121  const Point neigh_point = periodic->get_corresponding_pos(*my_node);
1122 
1123  // Figure out where my node lies on their reference element.
1124  const Point mapped_point = FEInterface::inverse_map(Dim-1, fe_type,
1125  neigh_side.get(),
1126  neigh_point);
1127 
1128  for (unsigned int their_side_n=0;
1129  their_side_n < n_side_nodes;
1130  their_side_n++)
1131  {
1132  libmesh_assert_less (their_side_n, FEInterface::n_dofs(Dim-1, fe_type, neigh_side->type()));
1133 
1134  const Node * their_node = neigh_nodes[their_side_n];
1135  libmesh_assert(their_node);
1136 
1137  const Real their_value = FEInterface::shape(Dim-1,
1138  fe_type,
1139  neigh_side->type(),
1140  their_side_n,
1141  mapped_point);
1142 
1143  // since we may be running this method concurrently
1144  // on multiple threads we need to acquire a lock
1145  // before modifying the shared constraint_row object.
1146  {
1147  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
1148 
1149  NodeConstraintRow & constraint_row =
1150  constraints[my_node].first;
1151 
1152  constraint_row.insert(std::make_pair(their_node,
1153  their_value));
1154  }
1155  }
1156  }
1157  }
1158  }
1159  }
1160  }
1161 }
libMesh::FEInterface::n_dofs
static unsigned int n_dofs(const unsigned int dim, const FEType &fe_t, const ElemType t)
Definition: fe_interface.C:454
libMesh::invalid_uint
const unsigned int invalid_uint
Definition: libmesh.h:245
mesh
MeshBase & mesh
Definition: mesh_communication.C:1245
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29
libMesh::FEInterface::shape
static Real shape(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int i, const Point &p)
Definition: fe_interface.C:657
libMesh::FEInterface::inverse_map
static Point inverse_map(const unsigned int dim, const FEType &fe_t, const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: fe_interface.C:590
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::NodeConstraintRow
std::map< const Node *, Real, std::less< const Node * >, Threads::scalable_allocator< std::pair< const Node *const, Real > > > NodeConstraintRow
Definition: dof_map.h:145

◆ compute_proj_constraints()

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::compute_proj_constraints ( DofConstraints &  constraints,
DofMap &  dof_map,
const unsigned int  variable_number,
const Elem *  elem 
)
staticinherited

Computes the constraint matrix contributions (for non-conforming adapted meshes) corresponding to variable number var_number, using generic projections.

Definition at line 1366 of file fe_base.C.

Referenced by libMesh::FE< Dim, LAGRANGE_VEC >::compute_constraints().

1370 {
1371  libmesh_assert(elem);
1372 
1373  const unsigned int Dim = elem->dim();
1374 
1375  // Only constrain elements in 2,3D.
1376  if (Dim == 1)
1377  return;
1378 
1379  // Only constrain active elements with this method
1380  if (!elem->active())
1381  return;
1382 
1383  const FEType & base_fe_type = dof_map.variable_type(variable_number);
1384 
1385  // Construct FE objects for this element and its neighbors.
1386  std::unique_ptr<FEGenericBase<OutputShape>> my_fe
1387  (FEGenericBase<OutputShape>::build(Dim, base_fe_type));
1388  const FEContinuity cont = my_fe->get_continuity();
1389 
1390  // We don't need to constrain discontinuous elements
1391  if (cont == DISCONTINUOUS)
1392  return;
1393  libmesh_assert (cont == C_ZERO || cont == C_ONE);
1394 
1395  std::unique_ptr<FEGenericBase<OutputShape>> neigh_fe
1396  (FEGenericBase<OutputShape>::build(Dim, base_fe_type));
1397 
1398  QGauss my_qface(Dim-1, base_fe_type.default_quadrature_order());
1399  my_fe->attach_quadrature_rule (&my_qface);
1400  std::vector<Point> neigh_qface;
1401 
1402  const std::vector<Real> & JxW = my_fe->get_JxW();
1403  const std::vector<Point> & q_point = my_fe->get_xyz();
1404  const std::vector<std::vector<OutputShape>> & phi = my_fe->get_phi();
1405  const std::vector<std::vector<OutputShape>> & neigh_phi =
1406  neigh_fe->get_phi();
1407  const std::vector<Point> * face_normals = nullptr;
1408  const std::vector<std::vector<OutputGradient>> * dphi = nullptr;
1409  const std::vector<std::vector<OutputGradient>> * neigh_dphi = nullptr;
1410 
1411  std::vector<dof_id_type> my_dof_indices, neigh_dof_indices;
1412  std::vector<unsigned int> my_side_dofs, neigh_side_dofs;
1413 
1414  if (cont != C_ZERO)
1415  {
1416  const std::vector<Point> & ref_face_normals =
1417  my_fe->get_normals();
1418  face_normals = &ref_face_normals;
1419  const std::vector<std::vector<OutputGradient>> & ref_dphi =
1420  my_fe->get_dphi();
1421  dphi = &ref_dphi;
1422  const std::vector<std::vector<OutputGradient>> & ref_neigh_dphi =
1423  neigh_fe->get_dphi();
1424  neigh_dphi = &ref_neigh_dphi;
1425  }
1426 
1427  DenseMatrix<Real> Ke;
1428  DenseVector<Real> Fe;
1429  std::vector<DenseVector<Real>> Ue;
1430 
1431  // Look at the element faces. Check to see if we need to
1432  // build constraints.
1433  for (auto s : elem->side_index_range())
1434  if (elem->neighbor_ptr(s) != nullptr)
1435  {
1436  // Get pointers to the element's neighbor.
1437  const Elem * neigh = elem->neighbor_ptr(s);
1438 
1439  // h refinement constraints:
1440  // constrain dofs shared between
1441  // this element and ones coarser
1442  // than this element.
1443  if (neigh->level() < elem->level())
1444  {
1445  unsigned int s_neigh = neigh->which_neighbor_am_i(elem);
1446  libmesh_assert_less (s_neigh, neigh->n_neighbors());
1447 
1448  // Find the minimum p level; we build the h constraint
1449  // matrix with this and then constrain away all higher p
1450  // DoFs.
1451  libmesh_assert(neigh->active());
1452  const unsigned int min_p_level =
1453  std::min(elem->p_level(), neigh->p_level());
1454 
1455  // we may need to make the FE objects reinit with the
1456  // minimum shared p_level
1457  const unsigned int old_elem_level = elem->p_level();
1458  if (elem->p_level() != min_p_level)
1459  my_fe->set_fe_order(my_fe->get_fe_type().order.get_order() - old_elem_level + min_p_level);
1460  const unsigned int old_neigh_level = neigh->p_level();
1461  if (old_neigh_level != min_p_level)
1462  neigh_fe->set_fe_order(neigh_fe->get_fe_type().order.get_order() - old_neigh_level + min_p_level);
1463 
1464  my_fe->reinit(elem, s);
1465 
1466  // This function gets called element-by-element, so there
1467  // will be a lot of memory allocation going on. We can
1468  // at least minimize this for the case of the dof indices
1469  // by efficiently preallocating the requisite storage.
1470  // n_nodes is not necessarily n_dofs, but it is better
1471  // than nothing!
1472  my_dof_indices.reserve (elem->n_nodes());
1473  neigh_dof_indices.reserve (neigh->n_nodes());
1474 
1475  dof_map.dof_indices (elem, my_dof_indices,
1476  variable_number,
1477  min_p_level);
1478  dof_map.dof_indices (neigh, neigh_dof_indices,
1479  variable_number,
1480  min_p_level);
1481 
1482  const unsigned int n_qp = my_qface.n_points();
1483 
1484  FEInterface::inverse_map (Dim, base_fe_type, neigh,
1485  q_point, neigh_qface);
1486 
1487  neigh_fe->reinit(neigh, &neigh_qface);
1488 
1489  // We're only concerned with DOFs whose values (and/or first
1490  // derivatives for C1 elements) are supported on side nodes
1491  FEType elem_fe_type = base_fe_type;
1492  if (old_elem_level != min_p_level)
1493  elem_fe_type.order = base_fe_type.order.get_order() - old_elem_level + min_p_level;
1494  FEType neigh_fe_type = base_fe_type;
1495  if (old_neigh_level != min_p_level)
1496  neigh_fe_type.order = base_fe_type.order.get_order() - old_neigh_level + min_p_level;
1497  FEInterface::dofs_on_side(elem, Dim, elem_fe_type, s, my_side_dofs);
1498  FEInterface::dofs_on_side(neigh, Dim, neigh_fe_type, s_neigh, neigh_side_dofs);
1499 
1500  const unsigned int n_side_dofs =
1501  cast_int<unsigned int>(my_side_dofs.size());
1502  libmesh_assert_equal_to (n_side_dofs, neigh_side_dofs.size());
1503 
1504  Ke.resize (n_side_dofs, n_side_dofs);
1505  Ue.resize(n_side_dofs);
1506 
1507  // Form the projection matrix, (inner product of fine basis
1508  // functions against fine test functions)
1509  for (unsigned int is = 0; is != n_side_dofs; ++is)
1510  {
1511  const unsigned int i = my_side_dofs[is];
1512  for (unsigned int js = 0; js != n_side_dofs; ++js)
1513  {
1514  const unsigned int j = my_side_dofs[js];
1515  for (unsigned int qp = 0; qp != n_qp; ++qp)
1516  {
1517  Ke(is,js) += JxW[qp] * TensorTools::inner_product(phi[i][qp], phi[j][qp]);
1518  if (cont != C_ZERO)
1519  Ke(is,js) += JxW[qp] *
1520  TensorTools::inner_product((*dphi)[i][qp] *
1521  (*face_normals)[qp],
1522  (*dphi)[j][qp] *
1523  (*face_normals)[qp]);
1524  }
1525  }
1526  }
1527 
1528  // Form the right hand sides, (inner product of coarse basis
1529  // functions against fine test functions)
1530  for (unsigned int is = 0; is != n_side_dofs; ++is)
1531  {
1532  const unsigned int i = neigh_side_dofs[is];
1533  Fe.resize (n_side_dofs);
1534  for (unsigned int js = 0; js != n_side_dofs; ++js)
1535  {
1536  const unsigned int j = my_side_dofs[js];
1537  for (unsigned int qp = 0; qp != n_qp; ++qp)
1538  {
1539  Fe(js) += JxW[qp] *
1540  TensorTools::inner_product(neigh_phi[i][qp],
1541  phi[j][qp]);
1542  if (cont != C_ZERO)
1543  Fe(js) += JxW[qp] *
1544  TensorTools::inner_product((*neigh_dphi)[i][qp] *
1545  (*face_normals)[qp],
1546  (*dphi)[j][qp] *
1547  (*face_normals)[qp]);
1548  }
1549  }
1550  Ke.cholesky_solve(Fe, Ue[is]);
1551  }
1552 
1553  for (unsigned int js = 0; js != n_side_dofs; ++js)
1554  {
1555  const unsigned int j = my_side_dofs[js];
1556  const dof_id_type my_dof_g = my_dof_indices[j];
1557  libmesh_assert_not_equal_to (my_dof_g, DofObject::invalid_id);
1558 
1559  // Hunt for "constraining against myself" cases before
1560  // we bother creating a constraint row
1561  bool self_constraint = false;
1562  for (unsigned int is = 0; is != n_side_dofs; ++is)
1563  {
1564  const unsigned int i = neigh_side_dofs[is];
1565  const dof_id_type their_dof_g = neigh_dof_indices[i];
1566  libmesh_assert_not_equal_to (their_dof_g, DofObject::invalid_id);
1567 
1568  if (their_dof_g == my_dof_g)
1569  {
1570 #ifndef NDEBUG
1571  const Real their_dof_value = Ue[is](js);
1572  libmesh_assert_less (std::abs(their_dof_value-1.),
1573  10*TOLERANCE);
1574 
1575  for (unsigned int k = 0; k != n_side_dofs; ++k)
1576  libmesh_assert(k == is ||
1577  std::abs(Ue[k](js)) <
1578  10*TOLERANCE);
1579 #endif
1580 
1581  self_constraint = true;
1582  break;
1583  }
1584  }
1585 
1586  if (self_constraint)
1587  continue;
1588 
1589  DofConstraintRow * constraint_row;
1590 
1591  // we may be running constraint methods concurrently
1592  // on multiple threads, so we need a lock to
1593  // ensure that this constraint is "ours"
1594  {
1595  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
1596 
1597  if (dof_map.is_constrained_dof(my_dof_g))
1598  continue;
1599 
1600  constraint_row = &(constraints[my_dof_g]);
1601  libmesh_assert(constraint_row->empty());
1602  }
1603 
1604  for (unsigned int is = 0; is != n_side_dofs; ++is)
1605  {
1606  const unsigned int i = neigh_side_dofs[is];
1607  const dof_id_type their_dof_g = neigh_dof_indices[i];
1608  libmesh_assert_not_equal_to (their_dof_g, DofObject::invalid_id);
1609  libmesh_assert_not_equal_to (their_dof_g, my_dof_g);
1610 
1611  const Real their_dof_value = Ue[is](js);
1612 
1613  if (std::abs(their_dof_value) < 10*TOLERANCE)
1614  continue;
1615 
1616  constraint_row->insert(std::make_pair(their_dof_g,
1617  their_dof_value));
1618  }
1619  }
1620 
1621  my_fe->set_fe_order(my_fe->get_fe_type().order.get_order() + old_elem_level - min_p_level);
1622  neigh_fe->set_fe_order(neigh_fe->get_fe_type().order.get_order() + old_neigh_level - min_p_level);
1623  }
1624 
1625  // p refinement constraints:
1626  // constrain dofs shared between
1627  // active elements and neighbors with
1628  // lower polynomial degrees
1629  const unsigned int min_p_level =
1630  neigh->min_p_level_by_neighbor(elem, elem->p_level());
1631  if (min_p_level < elem->p_level())
1632  {
1633  // Adaptive p refinement of non-hierarchic bases will
1634  // require more coding
1635  libmesh_assert(my_fe->is_hierarchic());
1636  dof_map.constrain_p_dofs(variable_number, elem,
1637  s, min_p_level);
1638  }
1639  }
1640 }
libMesh::FEType
Manages the family, order, etc. parameters for a given FE.
Definition: fe_type.h:179
std::abs
double abs(double a)
Definition: libmesh_augment_std_namespace.h:59
libMesh::Elem::side_index_range
IntRange< unsigned short > side_index_range() const
Definition: elem.h:2166
libMesh::DofMap::dof_indices
void dof_indices(const Elem *const elem, std::vector< dof_id_type > &di) const
Definition: dof_map.C:1930
libMesh::FEInterface::dofs_on_side
static void dofs_on_side(const Elem *const elem, const unsigned int dim, const FEType &fe_t, unsigned int s, std::vector< unsigned int > &di)
Definition: fe_interface.C:523
libMesh::DenseVector::resize
void resize(const unsigned int n)
Definition: dense_vector.h:355
libMesh::DofMap::variable_type
const FEType & variable_type(const unsigned int c) const
Definition: dof_map.h:1792
libMesh::Elem
The base class for all geometric element types.
Definition: elem.h:100
libMesh::FEType::default_quadrature_order
Order default_quadrature_order() const
Definition: fe_type.h:333
libMesh::Elem::p_level
unsigned int p_level() const
Definition: elem.h:2555
libMesh::FEType::order
OrderWrapper order
Definition: fe_type.h:198
libMesh::TOLERANCE
static const Real TOLERANCE
Definition: libmesh_common.h:139
libMesh::Elem::min_p_level_by_neighbor
unsigned int min_p_level_by_neighbor(const Elem *neighbor, unsigned int current_min) const
Definition: elem.C:1870
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498
libMesh::Elem::n_nodes
virtual unsigned int n_nodes() const =0
libMesh::Elem::which_neighbor_am_i
unsigned int which_neighbor_am_i(const Elem *e) const
Definition: elem.h:2314
libMesh::DofMap::is_constrained_dof
bool is_constrained_dof(const dof_id_type dof) const
Definition: dof_map.h:1829
libMesh::DofObject::invalid_id
static const dof_id_type invalid_id
Definition: dof_object.h:347
libMesh::FEInterface::inverse_map
static Point inverse_map(const unsigned int dim, const FEType &fe_t, const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: fe_interface.C:590
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503
libMesh::OrderWrapper::get_order
int get_order() const
Definition: fe_type.h:78
libMesh::Elem::neighbor_ptr
const Elem * neighbor_ptr(unsigned int i) const
Definition: elem.h:2050
libMesh::Elem::level
unsigned int level() const
Definition: elem.h:2521
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::Elem::dim
virtual unsigned short dim() const =0
libMesh::Elem::n_neighbors
unsigned int n_neighbors() const
Definition: elem.h:644
libMesh::DofConstraintRow
std::map< dof_id_type, Real, std::less< dof_id_type >, Threads::scalable_allocator< std::pair< const dof_id_type, Real > > > DofConstraintRow
Definition: dof_map.h:97
libMesh::DenseMatrix::resize
void resize(const unsigned int new_m, const unsigned int new_n)
Definition: dense_matrix.h:792
libMesh::QGauss
Implements 1, 2, and 3D "Gaussian" quadrature rules.
Definition: quadrature_gauss.h:39
libMesh::DenseMatrix::cholesky_solve
void cholesky_solve(const DenseVector< T2 > &b, DenseVector< T2 > &x)
Definition: dense_matrix_impl.h:929
libMesh::DenseMatrix
A matrix object used for finite element assembly and numerics.
Definition: dense_matrix.h:54
libMesh::Elem::active
bool active() const
Definition: elem.h:2390
std::min
long double min(long double a, double b)
Definition: libmesh_augment_std_namespace.h:29
libMesh::TensorTools::inner_product
boostcopy::enable_if_c< ScalarTraits< T >::value &&ScalarTraits< T2 >::value, typename CompareTypes< T, T2 >::supertype >::type inner_product(const T &a, const T2 &b)
Definition: tensor_tools.h:47
libMesh::DofMap::constrain_p_dofs
void constrain_p_dofs(unsigned int var, const Elem *elem, unsigned int s, unsigned int p)
Definition: dof_map_constraints.C:4208
libMesh::dof_id_type
uint8_t dof_id_type
Definition: id_types.h:64

◆ compute_shape_functions()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::compute_shape_functions ( const Elem *  ,
const std::vector< Point > &   
)
overrideprotectedvirtual

After having updated the jacobian and the transformation from local to global coordinates in FEAbstract::compute_map(), the first derivatives of the shape functions are transformed to global coordinates, giving dphi, dphidx/y/z, dphasedx/y/z, dweight. This method should barely be re-defined in derived classes, but still should be usable for children. Therefore, keep it protected.

Reimplemented from libMesh::FEGenericBase< OutputType >.

Definition at line 878 of file inf_fe.C.

References libMesh::index_range().

880 {
881  // Start logging the overall computation of shape functions
882  LOG_SCOPE("compute_shape_functions()", "InfFE");
883 
884  const unsigned int n_total_qp = _n_total_qp;
885 
886  // Compute the shape function values (and derivatives)
887  // at the Quadrature points. Note that the actual values
888  // have already been computed via init_shape_functions
889 
890  // Compute the value of the derivative shape function i at quadrature point p
891  switch (dim)
892  {
893 
894  case 1:
895  {
896  libmesh_not_implemented();
897  break;
898  }
899 
900  case 2:
901  {
902  libmesh_not_implemented();
903  break;
904  }
905 
906  case 3:
907  {
908  const std::vector<Real> & dxidx_map = this->_fe_map->get_dxidx();
909  const std::vector<Real> & dxidy_map = this->_fe_map->get_dxidy();
910  const std::vector<Real> & dxidz_map = this->_fe_map->get_dxidz();
911 
912  const std::vector<Real> & detadx_map = this->_fe_map->get_detadx();
913  const std::vector<Real> & detady_map = this->_fe_map->get_detady();
914  const std::vector<Real> & detadz_map = this->_fe_map->get_detadz();
915 
916  const std::vector<Real> & dzetadx_map = this->_fe_map->get_dzetadx();
917  const std::vector<Real> & dzetady_map = this->_fe_map->get_dzetady();
918  const std::vector<Real> & dzetadz_map = this->_fe_map->get_dzetadz();
919 
920  // These are _all_ shape functions of this infinite element
921  for (auto i : index_range(phi))
922  for (unsigned int p=0; p<n_total_qp; p++)
923  {
924  // dphi/dx = (dphi/dxi)*(dxi/dx) + (dphi/deta)*(deta/dx) + (dphi/dzeta)*(dzeta/dx);
925  dphi[i][p](0) =
926  dphidx[i][p] = (dphidxi[i][p]*dxidx_map[p] +
927  dphideta[i][p]*detadx_map[p] +
928  dphidzeta[i][p]*dzetadx_map[p]);
929 
930  // dphi/dy = (dphi/dxi)*(dxi/dy) + (dphi/deta)*(deta/dy) + (dphi/dzeta)*(dzeta/dy);
931  dphi[i][p](1) =
932  dphidy[i][p] = (dphidxi[i][p]*dxidy_map[p] +
933  dphideta[i][p]*detady_map[p] +
934  dphidzeta[i][p]*dzetady_map[p]);
935 
936  // dphi/dz = (dphi/dxi)*(dxi/dz) + (dphi/deta)*(deta/dz) + (dphi/dzeta)*(dzeta/dz);
937  dphi[i][p](2) =
938  dphidz[i][p] = (dphidxi[i][p]*dxidz_map[p] +
939  dphideta[i][p]*detadz_map[p] +
940  dphidzeta[i][p]*dzetadz_map[p]);
941  }
942 
943 
944  // This is the derivative of the phase term of this infinite element
945  for (unsigned int p=0; p<n_total_qp; p++)
946  {
947  // the derivative of the phase term
948  dphase[p](0) = (dphasedxi[p] * dxidx_map[p] +
949  dphasedeta[p] * detadx_map[p] +
950  dphasedzeta[p] * dzetadx_map[p]);
951 
952  dphase[p](1) = (dphasedxi[p] * dxidy_map[p] +
953  dphasedeta[p] * detady_map[p] +
954  dphasedzeta[p] * dzetady_map[p]);
955 
956  dphase[p](2) = (dphasedxi[p] * dxidz_map[p] +
957  dphasedeta[p] * detadz_map[p] +
958  dphasedzeta[p] * dzetadz_map[p]);
959 
960  // the derivative of the radial weight - varies only in radial direction,
961  // therefore dweightdxi = dweightdeta = 0.
962  dweight[p](0) = dweightdv[p] * dzetadx_map[p];
963 
964  dweight[p](1) = dweightdv[p] * dzetady_map[p];
965 
966  dweight[p](2) = dweightdv[p] * dzetadz_map[p];
967  }
968 
969  break;
970  }
971 
972  default:
973  libmesh_error_msg("Unsupported dim = " << dim);
974  }
975 }
libMesh::FEGenericBase::dphidxi
std::vector< std::vector< OutputShape > > dphidxi
Definition: fe_base.h:518
libMesh::FEGenericBase::dphidzeta
std::vector< std::vector< OutputShape > > dphidzeta
Definition: fe_base.h:528
libMesh::InfFE::dphasedxi
std::vector< Real > dphasedxi
Definition: inf_fe.h:664
libMesh::InfFE::dweightdv
std::vector< Real > dweightdv
Definition: inf_fe.h:620
libMesh::InfFE::_n_total_qp
unsigned int _n_total_qp
Definition: inf_fe.h:740
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::FEGenericBase::dphidy
std::vector< std::vector< OutputShape > > dphidy
Definition: fe_base.h:538
libMesh::FEGenericBase::dphidx
std::vector< std::vector< OutputShape > > dphidx
Definition: fe_base.h:533
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531
libMesh::FEGenericBase::dphase
std::vector< OutputGradient > dphase
Definition: fe_base.h:629
libMesh::InfFE::dphasedzeta
std::vector< Real > dphasedzeta
Definition: inf_fe.h:678
libMesh::InfFE::dphasedeta
std::vector< Real > dphasedeta
Definition: inf_fe.h:671
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525
libMesh::FEGenericBase::dphidz
std::vector< std::vector< OutputShape > > dphidz
Definition: fe_base.h:543
libMesh::FEGenericBase::dphideta
std::vector< std::vector< OutputShape > > dphideta
Definition: fe_base.h:523
libMesh::FEGenericBase::dweight
std::vector< RealGradient > dweight
Definition: fe_base.h:636

◆ compute_shape_indices()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::compute_shape_indices ( const FEType &  fet,
const ElemType  inf_elem_type,
const unsigned int  i,
unsigned int &  base_shape,
unsigned int &  radial_shape 
)
staticprotected

Computes the indices of shape functions in the base base_shape and in radial direction radial_shape (0 in the base, 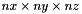$ \ge 1 $ further out) associated to the shape with global index i of an infinite element of type inf_elem_type.

Definition at line 677 of file inf_fe_static.C.

References libMesh::OrderWrapper::get_order(), libMesh::INFEDGE2, libMesh::INFHEX16, libMesh::INFHEX18, libMesh::INFHEX8, libMesh::INFPRISM12, libMesh::INFPRISM6, libMesh::INFQUAD4, libMesh::INFQUAD6, libMesh::invalid_uint, libMesh::FEInterface::n_dofs_at_node(), libMesh::FEInterface::n_dofs_per_elem(), and libMesh::FEType::radial_order.

682 {
683 
684  /*
685  * An example is provided: the numbers in comments refer to
686  * a fictitious InfHex18. The numbers are chosen as exemplary
687  * values. There is currently no base approximation that
688  * requires this many dof's at nodes, sides, faces and in the element.
689  *
690  * the order of the shape functions is heavily related with the
691  * order the dofs are assigned in \p DofMap::distributed_dofs().
692  * Due to the infinite elements with higher-order base approximation,
693  * some more effort is necessary.
694  *
695  * numbering scheme:
696  * 1. all vertices in the base, assign node->n_comp() dofs to each vertex
697  * 2. all vertices further out: innermost loop: radial shapes,
698  * then the base approximation shapes
699  * 3. all side nodes in the base, assign node->n_comp() dofs to each side node
700  * 4. all side nodes further out: innermost loop: radial shapes,
701  * then the base approximation shapes
702  * 5. (all) face nodes in the base, assign node->n_comp() dofs to each face node
703  * 6. (all) face nodes further out: innermost loop: radial shapes,
704  * then the base approximation shapes
705  * 7. element-associated dof in the base
706  * 8. element-associated dof further out
707  */
708 
709  const unsigned int radial_order = static_cast<unsigned int>(fet.radial_order.get_order()); // 4
710  const unsigned int radial_order_p_one = radial_order+1; // 5
711 
712  const ElemType base_elem_type (Base::get_elem_type(inf_elem_type)); // QUAD9
713 
714  // assume that the number of dof is the same for all vertices
715  unsigned int n_base_vertices = libMesh::invalid_uint; // 4
716  const unsigned int n_base_vertex_dof = FEInterface::n_dofs_at_node (Dim-1, fet, base_elem_type, 0);// 2
717 
718  unsigned int n_base_side_nodes = libMesh::invalid_uint; // 4
719  unsigned int n_base_side_dof = libMesh::invalid_uint; // 3
720 
721  unsigned int n_base_face_nodes = libMesh::invalid_uint; // 1
722  unsigned int n_base_face_dof = libMesh::invalid_uint; // 5
723 
724  const unsigned int n_base_elem_dof = FEInterface::n_dofs_per_elem (Dim-1, fet, base_elem_type);// 9
725 
726 
727  switch (inf_elem_type)
728  {
729  case INFEDGE2:
730  {
731  n_base_vertices = 1;
732  n_base_side_nodes = 0;
733  n_base_face_nodes = 0;
734  n_base_side_dof = 0;
735  n_base_face_dof = 0;
736  break;
737  }
738 
739  case INFQUAD4:
740  {
741  n_base_vertices = 2;
742  n_base_side_nodes = 0;
743  n_base_face_nodes = 0;
744  n_base_side_dof = 0;
745  n_base_face_dof = 0;
746  break;
747  }
748 
749  case INFQUAD6:
750  {
751  n_base_vertices = 2;
752  n_base_side_nodes = 1;
753  n_base_face_nodes = 0;
754  n_base_side_dof = FEInterface::n_dofs_at_node (Dim-1, fet,base_elem_type, n_base_vertices);
755  n_base_face_dof = 0;
756  break;
757  }
758 
759  case INFHEX8:
760  {
761  n_base_vertices = 4;
762  n_base_side_nodes = 0;
763  n_base_face_nodes = 0;
764  n_base_side_dof = 0;
765  n_base_face_dof = 0;
766  break;
767  }
768 
769  case INFHEX16:
770  {
771  n_base_vertices = 4;
772  n_base_side_nodes = 4;
773  n_base_face_nodes = 0;
774  n_base_side_dof = FEInterface::n_dofs_at_node (Dim-1, fet,base_elem_type, n_base_vertices);
775  n_base_face_dof = 0;
776  break;
777  }
778 
779  case INFHEX18:
780  {
781  n_base_vertices = 4;
782  n_base_side_nodes = 4;
783  n_base_face_nodes = 1;
784  n_base_side_dof = FEInterface::n_dofs_at_node (Dim-1, fet,base_elem_type, n_base_vertices);
785  n_base_face_dof = FEInterface::n_dofs_at_node (Dim-1, fet,base_elem_type, 8);
786  break;
787  }
788 
789 
790  case INFPRISM6:
791  {
792  n_base_vertices = 3;
793  n_base_side_nodes = 0;
794  n_base_face_nodes = 0;
795  n_base_side_dof = 0;
796  n_base_face_dof = 0;
797  break;
798  }
799 
800  case INFPRISM12:
801  {
802  n_base_vertices = 3;
803  n_base_side_nodes = 3;
804  n_base_face_nodes = 0;
805  n_base_side_dof = FEInterface::n_dofs_at_node (Dim-1, fet,base_elem_type, n_base_vertices);
806  n_base_face_dof = 0;
807  break;
808  }
809 
810  default:
811  libmesh_error_msg("Unrecognized inf_elem_type = " << inf_elem_type);
812  }
813 
814 
815  {
816  // these are the limits describing the intervals where the shape function lies
817  const unsigned int n_dof_at_base_vertices = n_base_vertices*n_base_vertex_dof; // 8
818  const unsigned int n_dof_at_all_vertices = n_dof_at_base_vertices*radial_order_p_one; // 40
819 
820  const unsigned int n_dof_at_base_sides = n_base_side_nodes*n_base_side_dof; // 12
821  const unsigned int n_dof_at_all_sides = n_dof_at_base_sides*radial_order_p_one; // 60
822 
823  const unsigned int n_dof_at_base_face = n_base_face_nodes*n_base_face_dof; // 5
824  const unsigned int n_dof_at_all_faces = n_dof_at_base_face*radial_order_p_one; // 25
825 
826 
827  // start locating the shape function
828  if (i < n_dof_at_base_vertices) // range of i: 0..7
829  {
830  // belongs to vertex in the base
831  radial_shape = 0;
832  base_shape = i;
833  }
834 
835  else if (i < n_dof_at_all_vertices) // range of i: 8..39
836  {
837  /* belongs to vertex in the outer shell
838  *
839  * subtract the number of dof already counted,
840  * so that i_offset contains only the offset for the base
841  */
842  const unsigned int i_offset = i - n_dof_at_base_vertices; // 0..31
843 
844  // first the radial dof are counted, then the base dof
845  radial_shape = (i_offset % radial_order) + 1;
846  base_shape = i_offset / radial_order;
847  }
848 
849  else if (i < n_dof_at_all_vertices+n_dof_at_base_sides) // range of i: 40..51
850  {
851  // belongs to base, is a side node
852  radial_shape = 0;
853  base_shape = i - radial_order * n_dof_at_base_vertices; // 8..19
854  }
855 
856  else if (i < n_dof_at_all_vertices+n_dof_at_all_sides) // range of i: 52..99
857  {
858  // belongs to side node in the outer shell
859  const unsigned int i_offset = i - (n_dof_at_all_vertices
860  + n_dof_at_base_sides); // 0..47
861  radial_shape = (i_offset % radial_order) + 1;
862  base_shape = (i_offset / radial_order) + n_dof_at_base_vertices;
863  }
864 
865  else if (i < n_dof_at_all_vertices+n_dof_at_all_sides+n_dof_at_base_face) // range of i: 100..104
866  {
867  // belongs to the node in the base face
868  radial_shape = 0;
869  base_shape = i - radial_order*(n_dof_at_base_vertices
870  + n_dof_at_base_sides); // 20..24
871  }
872 
873  else if (i < n_dof_at_all_vertices+n_dof_at_all_sides+n_dof_at_all_faces) // range of i: 105..124
874  {
875  // belongs to the node in the outer face
876  const unsigned int i_offset = i - (n_dof_at_all_vertices
877  + n_dof_at_all_sides
878  + n_dof_at_base_face); // 0..19
879  radial_shape = (i_offset % radial_order) + 1;
880  base_shape = (i_offset / radial_order) + n_dof_at_base_vertices + n_dof_at_base_sides;
881  }
882 
883  else if (i < n_dof_at_all_vertices+n_dof_at_all_sides+n_dof_at_all_faces+n_base_elem_dof) // range of i: 125..133
884  {
885  // belongs to the base and is an element associated shape
886  radial_shape = 0;
887  base_shape = i - (n_dof_at_all_vertices
888  + n_dof_at_all_sides
889  + n_dof_at_all_faces); // 0..8
890  }
891 
892  else // range of i: 134..169
893  {
894  libmesh_assert_less (i, n_dofs(fet, inf_elem_type));
895  // belongs to the outer shell and is an element associated shape
896  const unsigned int i_offset = i - (n_dof_at_all_vertices
897  + n_dof_at_all_sides
898  + n_dof_at_all_faces
899  + n_base_elem_dof); // 0..19
900  radial_shape = (i_offset % radial_order) + 1;
901  base_shape = (i_offset / radial_order) + n_dof_at_base_vertices + n_dof_at_base_sides + n_dof_at_base_face;
902  }
903  }
904 
905  return;
906 }
libMesh::FEInterface::n_dofs_per_elem
static unsigned int n_dofs_per_elem(const unsigned int dim, const FEType &fe_t, const ElemType t)
Definition: fe_interface.C:504
libMesh::invalid_uint
const unsigned int invalid_uint
Definition: libmesh.h:245
libMesh::InfFE::Base::get_elem_type
static ElemType get_elem_type(const ElemType type)
Definition: inf_fe_base_radial.C:51
libMesh::InfFE::n_dofs
static unsigned int n_dofs(const FEType &fet, const ElemType inf_elem_type)
Definition: inf_fe_static.C:55
libMesh::FEInterface::n_dofs_at_node
static unsigned int n_dofs_at_node(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int n)
Definition: fe_interface.C:473

◆ determine_calculations()

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::determine_calculations ( )
protectedinherited

Determine which values are to be calculated, for both the FE itself and for the FEMap.

Definition at line 728 of file fe_base.C.

729 {
730  this->calculations_started = true;
731 
732  // If the user forgot to request anything, we'll be safe and
733  // calculate everything:
734 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
735  if (!this->calculate_phi && !this->calculate_dphi && !this->calculate_d2phi
736  && !this->calculate_curl_phi && !this->calculate_div_phi)
737  {
738  this->calculate_phi = this->calculate_dphi = this->calculate_d2phi = this->calculate_dphiref = true;
739  if (FEInterface::field_type(fe_type.family) == TYPE_VECTOR)
740  {
741  this->calculate_curl_phi = true;
742  this->calculate_div_phi = true;
743  }
744  }
745 #else
746  if (!this->calculate_phi && !this->calculate_dphi && !this->calculate_curl_phi && !this->calculate_div_phi)
747  {
748  this->calculate_phi = this->calculate_dphi = this->calculate_dphiref = true;
749  if (FEInterface::field_type(fe_type.family) == TYPE_VECTOR)
750  {
751  this->calculate_curl_phi = true;
752  this->calculate_div_phi = true;
753  }
754  }
755 #endif // LIBMESH_ENABLE_SECOND_DERIVATIVES
756 
757  // Request whichever terms are necessary from the FEMap
758  if (this->calculate_phi)
759  this->_fe_trans->init_map_phi(*this);
760 
761  if (this->calculate_dphiref)
762  this->_fe_trans->init_map_dphi(*this);
763 
764 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
765  if (this->calculate_d2phi)
766  this->_fe_trans->init_map_d2phi(*this);
767 #endif //LIBMESH_ENABLE_SECOND_DERIVATIVES
768 }
libMesh::FEType::family
FEFamily family
Definition: fe_type.h:204
libMesh::FEGenericBase::_fe_trans
std::unique_ptr< FETransformationBase< OutputType > > _fe_trans
Definition: fe_base.h:493
libMesh::FEInterface::field_type
static FEFieldType field_type(const FEType &fe_type)
Definition: fe_interface.C:1437

◆ disable_print_counter_info()

void libMesh::ReferenceCounter::disable_print_counter_info ( )
staticinherited

Definition at line 106 of file reference_counter.C.

References libMesh::ReferenceCounter::_enable_print_counter.

Referenced by libMesh::LibMeshInit::LibMeshInit().

107 {
108  _enable_print_counter = false;
109  return;
110 }

◆ edge_reinit()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_base>
void libMesh::InfFE< Dim, T_radial, T_base >::edge_reinit ( const Elem *  elem,
const unsigned int  edge,
const Real  tolerance = TOLERANCE,
const std::vector< Point > *const  pts = nullptr,
const std::vector< Real > *const  weights = nullptr 
)
overridevirtual

Not implemented yet. Reinitializes all the physical element-dependent data based on the edge of an infinite element.

Implements libMesh::FEAbstract.

Definition at line 104 of file inf_fe_boundary.C.

109 {
110  // We don't do this for 1D elements!
111  //libmesh_assert_not_equal_to (Dim, 1);
112  libmesh_not_implemented_msg("ERROR: Edge conditions for infinite elements not implemented!");
113 
114  if (pts != nullptr)
115  libmesh_not_implemented_msg("ERROR: User-specified points for infinite elements not implemented!");
116 }

◆ enable_print_counter_info()

void libMesh::ReferenceCounter::enable_print_counter_info ( )
staticinherited

Methods to enable/disable the reference counter output from print_info()

Definition at line 100 of file reference_counter.C.

References libMesh::ReferenceCounter::_enable_print_counter.

101 {
102  _enable_print_counter = true;
103  return;
104 }

◆ eval() [1/16]

template<>
Real libMesh::InfFE< 1, INFINITE_MAP, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 69 of file inf_fe_map_eval.C.

69 { return infinite_map_eval(v, i); }

◆ eval() [2/16]

template<>
Real libMesh::InfFE< 2, INFINITE_MAP, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 70 of file inf_fe_map_eval.C.

70 { return infinite_map_eval(v, i); }

◆ eval() [3/16]

template<>
Real libMesh::InfFE< 3, INFINITE_MAP, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 71 of file inf_fe_map_eval.C.

71 { return infinite_map_eval(v, i); }

◆ eval() [4/16]

template<>
Real libMesh::InfFE< 1, LEGENDRE, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 310 of file inf_fe_legendre_eval.C.

310 { return legendre_eval(v, i); }

◆ eval() [5/16]

template<>
Real libMesh::InfFE< 2, LEGENDRE, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 311 of file inf_fe_legendre_eval.C.

311 { return legendre_eval(v, i); }

◆ eval() [6/16]

template<>
Real libMesh::InfFE< 3, LEGENDRE, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 312 of file inf_fe_legendre_eval.C.

312 { return legendre_eval(v, i); }

◆ eval() [7/16]

template<>
Real libMesh::InfFE< 1, JACOBI_30_00, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 457 of file inf_fe_jacobi_30_00_eval.C.

457 { return jacobi_30_00_eval(v, i); }

◆ eval() [8/16]

template<>
Real libMesh::InfFE< 2, JACOBI_30_00, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 458 of file inf_fe_jacobi_30_00_eval.C.

458 { return jacobi_30_00_eval(v, i); }

◆ eval() [9/16]

template<>
Real libMesh::InfFE< 3, JACOBI_30_00, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 459 of file inf_fe_jacobi_30_00_eval.C.

459 { return jacobi_30_00_eval(v, i); }

◆ eval() [10/16]

template<>
Real libMesh::InfFE< 1, JACOBI_20_00, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 462 of file inf_fe_jacobi_20_00_eval.C.

462 { return jacobi_20_00_eval(v, i); }

◆ eval() [11/16]

template<>
Real libMesh::InfFE< 2, JACOBI_20_00, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 463 of file inf_fe_jacobi_20_00_eval.C.

463 { return jacobi_20_00_eval(v, i); }

◆ eval() [12/16]

template<>
Real libMesh::InfFE< 3, JACOBI_20_00, CARTESIAN >::eval ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 464 of file inf_fe_jacobi_20_00_eval.C.

464 { return jacobi_20_00_eval(v, i); }

◆ eval() [13/16]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
static Real libMesh::InfFE< Dim, T_radial, T_map >::eval ( Real  v,
Order  o_radial,
unsigned int  i 
)
staticprotected
Returns
The value of the 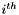$ i^{th} $ polynomial evaluated at v. This method provides the approximation in radial direction for the overall shape functions, which is defined in InfFE::shape(). This method is allowed to be static, since it is independent of dimension and base_family. It is templated, though, w.r.t. to radial FEFamily.
The value of the 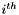$ i^{th} $ mapping shape function in radial direction evaluated at v when T_radial == INFINITE_MAP. Currently, only one specific mapping shape is used. Namely the one by Marques JMMC, Owen DRJ: Infinite elements in quasi-static materially nonlinear problems, Computers and Structures, 1984.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::compute_data(), libMesh::InfFE< Dim, T_radial, T_map >::init_radial_shape_functions(), and libMesh::InfFE< Dim, T_radial, T_map >::shape().

◆ eval() [14/16]

template<>
Real libMesh::InfFE< 1, LAGRANGE, CARTESIAN >::eval ( Real  v,
Order  o,
unsigned  i 
)
protected

Definition at line 2607 of file inf_fe_lagrange_eval.C.

2607 { return lagrange_eval(v, o, i); }

◆ eval() [15/16]

template<>
Real libMesh::InfFE< 2, LAGRANGE, CARTESIAN >::eval ( Real  v,
Order  o,
unsigned  i 
)
protected

Definition at line 2608 of file inf_fe_lagrange_eval.C.

2608 { return lagrange_eval(v, o, i); }

◆ eval() [16/16]

template<>
Real libMesh::InfFE< 3, LAGRANGE, CARTESIAN >::eval ( Real  v,
Order  o,
unsigned  i 
)
protected

Definition at line 2609 of file inf_fe_lagrange_eval.C.

2609 { return lagrange_eval(v, o, i); }

◆ eval_deriv() [1/16]

template<>
Real libMesh::InfFE< 1, INFINITE_MAP, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 75 of file inf_fe_map_eval.C.

75 { return infinite_map_eval_deriv(v, i); }

◆ eval_deriv() [2/16]

template<>
Real libMesh::InfFE< 2, INFINITE_MAP, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 76 of file inf_fe_map_eval.C.

76 { return infinite_map_eval_deriv(v, i); }

◆ eval_deriv() [3/16]

template<>
Real libMesh::InfFE< 3, INFINITE_MAP, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 77 of file inf_fe_map_eval.C.

77 { return infinite_map_eval_deriv(v, i); }

◆ eval_deriv() [4/16]

template<>
Real libMesh::InfFE< 1, LEGENDRE, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 316 of file inf_fe_legendre_eval.C.

316 { return legendre_eval_deriv(v, i); }

◆ eval_deriv() [5/16]

template<>
Real libMesh::InfFE< 2, LEGENDRE, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 317 of file inf_fe_legendre_eval.C.

317 { return legendre_eval_deriv(v, i); }

◆ eval_deriv() [6/16]

template<>
Real libMesh::InfFE< 3, LEGENDRE, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 318 of file inf_fe_legendre_eval.C.

318 { return legendre_eval_deriv(v, i); }

◆ eval_deriv() [7/16]

template<>
Real libMesh::InfFE< 1, JACOBI_30_00, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 463 of file inf_fe_jacobi_30_00_eval.C.

463 { return jacobi_30_00_eval_deriv(v, i); }

◆ eval_deriv() [8/16]

template<>
Real libMesh::InfFE< 2, JACOBI_30_00, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 464 of file inf_fe_jacobi_30_00_eval.C.

464 { return jacobi_30_00_eval_deriv(v, i); }

◆ eval_deriv() [9/16]

template<>
Real libMesh::InfFE< 3, JACOBI_30_00, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 465 of file inf_fe_jacobi_30_00_eval.C.

465 { return jacobi_30_00_eval_deriv(v, i); }

◆ eval_deriv() [10/16]

template<>
Real libMesh::InfFE< 1, JACOBI_20_00, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 468 of file inf_fe_jacobi_20_00_eval.C.

468 { return jacobi_20_00_eval_deriv(v, i); }

◆ eval_deriv() [11/16]

template<>
Real libMesh::InfFE< 2, JACOBI_20_00, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 469 of file inf_fe_jacobi_20_00_eval.C.

469 { return jacobi_20_00_eval_deriv(v, i); }

◆ eval_deriv() [12/16]

template<>
Real libMesh::InfFE< 3, JACOBI_20_00, CARTESIAN >::eval_deriv ( Real  v,
Order  ,
unsigned  i 
)
protected

Definition at line 470 of file inf_fe_jacobi_20_00_eval.C.

470 { return jacobi_20_00_eval_deriv(v, i); }

◆ eval_deriv() [13/16]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
static Real libMesh::InfFE< Dim, T_radial, T_map >::eval_deriv ( Real  v,
Order  o_radial,
unsigned int  i 
)
staticprotected
Returns
The value of the first derivative of the 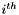$ i^{th} $ polynomial at coordinate v. See eval for details.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::init_radial_shape_functions().

◆ eval_deriv() [14/16]

template<>
Real libMesh::InfFE< 1, LAGRANGE, CARTESIAN >::eval_deriv ( Real  v,
Order  o,
unsigned  i 
)
protected

Definition at line 2613 of file inf_fe_lagrange_eval.C.

2613 { return lagrange_eval_deriv(v, o, i); }

◆ eval_deriv() [15/16]

template<>
Real libMesh::InfFE< 2, LAGRANGE, CARTESIAN >::eval_deriv ( Real  v,
Order  o,
unsigned  i 
)
protected

Definition at line 2614 of file inf_fe_lagrange_eval.C.

2614 { return lagrange_eval_deriv(v, o, i); }

◆ eval_deriv() [16/16]

template<>
Real libMesh::InfFE< 3, LAGRANGE, CARTESIAN >::eval_deriv ( Real  v,
Order  o,
unsigned  i 
)
protected

Definition at line 2615 of file inf_fe_lagrange_eval.C.

2615 { return lagrange_eval_deriv(v, o, i); }

◆ get_continuity()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
virtual FEContinuity libMesh::InfFE< Dim, T_radial, T_map >::get_continuity ( ) const
inlineoverridevirtual
Returns
The continuity of the element.

Implements libMesh::FEAbstract.

Definition at line 332 of file inf_fe.h.

References libMesh::C_ZERO.

333  { return C_ZERO; } // FIXME - is this true??

◆ get_curl_phi()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_curl_phi ( ) const
inlineinherited
Returns
The curl of the shape function at the quadrature points.

Definition at line 223 of file fe_base.h.

Referenced by libMesh::ExactSolution::_compute_error(), and libMesh::FEMContext::interior_curl().

224  { libmesh_assert(!calculations_started || calculate_curl_phi);
225  calculate_curl_phi = calculate_dphiref = true; return curl_phi; }
libMesh::FEGenericBase::curl_phi
std::vector< std::vector< OutputShape > > curl_phi
Definition: fe_base.h:508

◆ get_curvatures()

const std::vector<Real>& libMesh::FEAbstract::get_curvatures ( ) const
inlineinherited
Returns
The curvatures for use in face integration.

Definition at line 391 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

392  { return this->_fe_map->get_curvatures();}
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_d2phi()

template<typename OutputType>
const std::vector<std::vector<OutputTensor> >& libMesh::FEGenericBase< OutputType >::get_d2phi ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 289 of file fe_base.h.

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::System::calculate_norm(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::LaplacianErrorEstimator::init_context(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::FEMContext::interior_hessians(), libMesh::LaplacianErrorEstimator::internal_side_integration(), libMesh::FEMContext::side_hessians(), and libMesh::FEMContext::some_hessian().

290  { libmesh_assert(!calculations_started || calculate_d2phi);
291  calculate_d2phi = calculate_dphiref = true; return d2phi; }
libMesh::FEGenericBase::d2phi
std::vector< std::vector< OutputTensor > > d2phi
Definition: fe_base.h:551

◆ get_d2phideta2()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phideta2 ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points, in reference coordinates

Definition at line 369 of file fe_base.h.

Referenced by libMesh::H1FETransformation< OutputShape >::map_d2phi().

370  { libmesh_assert(!calculations_started || calculate_d2phi);
371  calculate_d2phi = calculate_dphiref = true; return d2phideta2; }
libMesh::FEGenericBase::d2phideta2
std::vector< std::vector< OutputShape > > d2phideta2
Definition: fe_base.h:571

◆ get_d2phidetadzeta()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidetadzeta ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points, in reference coordinates

Definition at line 377 of file fe_base.h.

Referenced by libMesh::H1FETransformation< OutputShape >::map_d2phi().

378  { libmesh_assert(!calculations_started || calculate_d2phi);
379  calculate_d2phi = calculate_dphiref = true; return d2phidetadzeta; }
libMesh::FEGenericBase::d2phidetadzeta
std::vector< std::vector< OutputShape > > d2phidetadzeta
Definition: fe_base.h:576

◆ get_d2phidx2()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidx2 ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 297 of file fe_base.h.

298  { libmesh_assert(!calculations_started || calculate_d2phi);
299  calculate_d2phi = calculate_dphiref = true; return d2phidx2; }
libMesh::FEGenericBase::d2phidx2
std::vector< std::vector< OutputShape > > d2phidx2
Definition: fe_base.h:586

◆ get_d2phidxdy()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidxdy ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 305 of file fe_base.h.

306  { libmesh_assert(!calculations_started || calculate_d2phi);
307  calculate_d2phi = calculate_dphiref = true; return d2phidxdy; }
libMesh::FEGenericBase::d2phidxdy
std::vector< std::vector< OutputShape > > d2phidxdy
Definition: fe_base.h:591

◆ get_d2phidxdz()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidxdz ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 313 of file fe_base.h.

314  { libmesh_assert(!calculations_started || calculate_d2phi);
315  calculate_d2phi = calculate_dphiref = true; return d2phidxdz; }
libMesh::FEGenericBase::d2phidxdz
std::vector< std::vector< OutputShape > > d2phidxdz
Definition: fe_base.h:596

◆ get_d2phidxi2()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidxi2 ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points, in reference coordinates

Definition at line 345 of file fe_base.h.

Referenced by libMesh::H1FETransformation< OutputShape >::map_d2phi().

346  { libmesh_assert(!calculations_started || calculate_d2phi);
347  calculate_d2phi = calculate_dphiref = true; return d2phidxi2; }
libMesh::FEGenericBase::d2phidxi2
std::vector< std::vector< OutputShape > > d2phidxi2
Definition: fe_base.h:556

◆ get_d2phidxideta()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidxideta ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points, in reference coordinates

Definition at line 353 of file fe_base.h.

Referenced by libMesh::H1FETransformation< OutputShape >::map_d2phi().

354  { libmesh_assert(!calculations_started || calculate_d2phi);
355  calculate_d2phi = calculate_dphiref = true; return d2phidxideta; }
libMesh::FEGenericBase::d2phidxideta
std::vector< std::vector< OutputShape > > d2phidxideta
Definition: fe_base.h:561

◆ get_d2phidxidzeta()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidxidzeta ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points, in reference coordinates

Definition at line 361 of file fe_base.h.

Referenced by libMesh::H1FETransformation< OutputShape >::map_d2phi().

362  { libmesh_assert(!calculations_started || calculate_d2phi);
363  calculate_d2phi = calculate_dphiref = true; return d2phidxidzeta; }
libMesh::FEGenericBase::d2phidxidzeta
std::vector< std::vector< OutputShape > > d2phidxidzeta
Definition: fe_base.h:566

◆ get_d2phidy2()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidy2 ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 321 of file fe_base.h.

322  { libmesh_assert(!calculations_started || calculate_d2phi);
323  calculate_d2phi = calculate_dphiref = true; return d2phidy2; }
libMesh::FEGenericBase::d2phidy2
std::vector< std::vector< OutputShape > > d2phidy2
Definition: fe_base.h:601

◆ get_d2phidydz()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidydz ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 329 of file fe_base.h.

330  { libmesh_assert(!calculations_started || calculate_d2phi);
331  calculate_d2phi = calculate_dphiref = true; return d2phidydz; }
libMesh::FEGenericBase::d2phidydz
std::vector< std::vector< OutputShape > > d2phidydz
Definition: fe_base.h:606

◆ get_d2phidz2()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidz2 ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points.

Definition at line 337 of file fe_base.h.

338  { libmesh_assert(!calculations_started || calculate_d2phi);
339  calculate_d2phi = calculate_dphiref = true; return d2phidz2; }
libMesh::FEGenericBase::d2phidz2
std::vector< std::vector< OutputShape > > d2phidz2
Definition: fe_base.h:611

◆ get_d2phidzeta2()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_d2phidzeta2 ( ) const
inlineinherited
Returns
The shape function second derivatives at the quadrature points, in reference coordinates

Definition at line 385 of file fe_base.h.

Referenced by libMesh::H1FETransformation< OutputShape >::map_d2phi().

386  { libmesh_assert(!calculations_started || calculate_d2phi);
387  calculate_d2phi = calculate_dphiref = true; return d2phidzeta2; }
libMesh::FEGenericBase::d2phidzeta2
std::vector< std::vector< OutputShape > > d2phidzeta2
Definition: fe_base.h:581

◆ get_d2xyzdeta2()

const std::vector<RealGradient>& libMesh::FEAbstract::get_d2xyzdeta2 ( ) const
inlineinherited
Returns
The second partial derivatives in eta.

Definition at line 278 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

279  { return this->_fe_map->get_d2xyzdeta2(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_d2xyzdetadzeta()

const std::vector<RealGradient>& libMesh::FEAbstract::get_d2xyzdetadzeta ( ) const
inlineinherited
Returns
The second partial derivatives in eta-zeta.

Definition at line 308 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

309  { return this->_fe_map->get_d2xyzdetadzeta(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_d2xyzdxi2()

const std::vector<RealGradient>& libMesh::FEAbstract::get_d2xyzdxi2 ( ) const
inlineinherited
Returns
The second partial derivatives in xi.

Definition at line 272 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

273  { return this->_fe_map->get_d2xyzdxi2(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_d2xyzdxideta()

const std::vector<RealGradient>& libMesh::FEAbstract::get_d2xyzdxideta ( ) const
inlineinherited
Returns
The second partial derivatives in xi-eta.

Definition at line 294 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

295  { return this->_fe_map->get_d2xyzdxideta(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_d2xyzdxidzeta()

const std::vector<RealGradient>& libMesh::FEAbstract::get_d2xyzdxidzeta ( ) const
inlineinherited
Returns
The second partial derivatives in xi-zeta.

Definition at line 302 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

303  { return this->_fe_map->get_d2xyzdxidzeta(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_d2xyzdzeta2()

const std::vector<RealGradient>& libMesh::FEAbstract::get_d2xyzdzeta2 ( ) const
inlineinherited
Returns
The second partial derivatives in zeta.

Definition at line 286 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

287  { return this->_fe_map->get_d2xyzdzeta2(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_detadx()

const std::vector<Real>& libMesh::FEAbstract::get_detadx ( ) const
inlineinherited
Returns
The deta/dx entry in the transformation matrix from physical to local coordinates.

Definition at line 338 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

339  { return this->_fe_map->get_detadx(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_detady()

const std::vector<Real>& libMesh::FEAbstract::get_detady ( ) const
inlineinherited
Returns
The deta/dy entry in the transformation matrix from physical to local coordinates.

Definition at line 345 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

346  { return this->_fe_map->get_detady(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_detadz()

const std::vector<Real>& libMesh::FEAbstract::get_detadz ( ) const
inlineinherited
Returns
The deta/dz entry in the transformation matrix from physical to local coordinates.

Definition at line 352 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

353  { return this->_fe_map->get_detadz(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dim()

unsigned int libMesh::FEAbstract::get_dim ( ) const
inlineinherited
Returns
the dimension of this FE

Definition at line 231 of file fe_abstract.h.

References libMesh::FEAbstract::dim.

232  { return dim; }
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531

◆ get_div_phi()

template<typename OutputType>
const std::vector<std::vector<OutputDivergence> >& libMesh::FEGenericBase< OutputType >::get_div_phi ( ) const
inlineinherited
Returns
The divergence of the shape function at the quadrature points.

Definition at line 231 of file fe_base.h.

Referenced by libMesh::ExactSolution::_compute_error(), and libMesh::FEMContext::interior_div().

232  { libmesh_assert(!calculations_started || calculate_div_phi);
233  calculate_div_phi = calculate_dphiref = true; return div_phi; }
libMesh::FEGenericBase::div_phi
std::vector< std::vector< OutputDivergence > > div_phi
Definition: fe_base.h:513

◆ get_dphase()

template<typename OutputType>
const std::vector<OutputGradient>& libMesh::FEGenericBase< OutputType >::get_dphase ( ) const
inlineinherited
Returns
The global first derivative of the phase term which is used in infinite elements, evaluated at the quadrature points.

In case of the general finite element class FE this field is initialized to all zero, so that the variational formulation for an infinite element produces correct element matrices for a mesh using both finite and infinite elements.

Definition at line 403 of file fe_base.h.

404  { return dphase; }
libMesh::FEGenericBase::dphase
std::vector< OutputGradient > dphase
Definition: fe_base.h:629

◆ get_dphi()

template<typename OutputType>
const std::vector<std::vector<OutputGradient> >& libMesh::FEGenericBase< OutputType >::get_dphi ( ) const
inlineinherited
Returns
The shape function derivatives at the quadrature points.

Definition at line 215 of file fe_base.h.

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::System::calculate_norm(), libMesh::OldSolutionCoefs< Output, point_output >::eval_at_point(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::OldSolutionBase< Output, point_output >::get_shape_outputs(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::KellyErrorEstimator::init_context(), libMesh::FEMContext::interior_gradients(), libMesh::KellyErrorEstimator::internal_side_integration(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), libMesh::FEMContext::side_gradient(), libMesh::FEMContext::side_gradients(), and libMesh::FEMContext::some_gradient().

216  { libmesh_assert(!calculations_started || calculate_dphi);
217  calculate_dphi = calculate_dphiref = true; return dphi; }
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503

◆ get_dphideta()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_dphideta ( ) const
inlineinherited
Returns
The shape function eta-derivative at the quadrature points.

Definition at line 271 of file fe_base.h.

Referenced by libMesh::HCurlFETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_d2phi(), libMesh::H1FETransformation< OutputShape >::map_div(), and libMesh::H1FETransformation< OutputShape >::map_dphi().

272  { libmesh_assert(!calculations_started || calculate_dphiref);
273  calculate_dphiref = true; return dphideta; }
libMesh::FEGenericBase::dphideta
std::vector< std::vector< OutputShape > > dphideta
Definition: fe_base.h:523

◆ get_dphidx()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_dphidx ( ) const
inlineinherited
Returns
The shape function x-derivative at the quadrature points.

Definition at line 239 of file fe_base.h.

240  { libmesh_assert(!calculations_started || calculate_dphi);
241  calculate_dphi = calculate_dphiref = true; return dphidx; }
libMesh::FEGenericBase::dphidx
std::vector< std::vector< OutputShape > > dphidx
Definition: fe_base.h:533

◆ get_dphidxi()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_dphidxi ( ) const
inlineinherited
Returns
The shape function xi-derivative at the quadrature points.

Definition at line 263 of file fe_base.h.

Referenced by libMesh::HCurlFETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_d2phi(), libMesh::H1FETransformation< OutputShape >::map_div(), and libMesh::H1FETransformation< OutputShape >::map_dphi().

264  { libmesh_assert(!calculations_started || calculate_dphiref);
265  calculate_dphiref = true; return dphidxi; }
libMesh::FEGenericBase::dphidxi
std::vector< std::vector< OutputShape > > dphidxi
Definition: fe_base.h:518

◆ get_dphidy()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_dphidy ( ) const
inlineinherited
Returns
The shape function y-derivative at the quadrature points.

Definition at line 247 of file fe_base.h.

248  { libmesh_assert(!calculations_started || calculate_dphi);
249  calculate_dphi = calculate_dphiref = true; return dphidy; }
libMesh::FEGenericBase::dphidy
std::vector< std::vector< OutputShape > > dphidy
Definition: fe_base.h:538

◆ get_dphidz()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_dphidz ( ) const
inlineinherited
Returns
The shape function z-derivative at the quadrature points.

Definition at line 255 of file fe_base.h.

256  { libmesh_assert(!calculations_started || calculate_dphi);
257  calculate_dphi = calculate_dphiref = true; return dphidz; }
libMesh::FEGenericBase::dphidz
std::vector< std::vector< OutputShape > > dphidz
Definition: fe_base.h:543

◆ get_dphidzeta()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_dphidzeta ( ) const
inlineinherited
Returns
The shape function zeta-derivative at the quadrature points.

Definition at line 279 of file fe_base.h.

Referenced by libMesh::HCurlFETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_d2phi(), libMesh::H1FETransformation< OutputShape >::map_div(), and libMesh::H1FETransformation< OutputShape >::map_dphi().

280  { libmesh_assert(!calculations_started || calculate_dphiref);
281  calculate_dphiref = true; return dphidzeta; }
libMesh::FEGenericBase::dphidzeta
std::vector< std::vector< OutputShape > > dphidzeta
Definition: fe_base.h:528

◆ get_dxidx()

const std::vector<Real>& libMesh::FEAbstract::get_dxidx ( ) const
inlineinherited
Returns
The dxi/dx entry in the transformation matrix from physical to local coordinates.

Definition at line 317 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

318  { return this->_fe_map->get_dxidx(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dxidy()

const std::vector<Real>& libMesh::FEAbstract::get_dxidy ( ) const
inlineinherited
Returns
The dxi/dy entry in the transformation matrix from physical to local coordinates.

Definition at line 324 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

325  { return this->_fe_map->get_dxidy(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dxidz()

const std::vector<Real>& libMesh::FEAbstract::get_dxidz ( ) const
inlineinherited
Returns
The dxi/dz entry in the transformation matrix from physical to local coordinates.

Definition at line 331 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

332  { return this->_fe_map->get_dxidz(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dxyzdeta()

const std::vector<RealGradient>& libMesh::FEAbstract::get_dxyzdeta ( ) const
inlineinherited
Returns
The element tangents in eta-direction at the quadrature points.

Definition at line 259 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

260  { return this->_fe_map->get_dxyzdeta(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dxyzdxi()

const std::vector<RealGradient>& libMesh::FEAbstract::get_dxyzdxi ( ) const
inlineinherited
Returns
The element tangents in xi-direction at the quadrature points.

Definition at line 252 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

253  { return this->_fe_map->get_dxyzdxi(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dxyzdzeta()

const std::vector<RealGradient>& libMesh::FEAbstract::get_dxyzdzeta ( ) const
inlineinherited
Returns
The element tangents in zeta-direction at the quadrature points.

Definition at line 266 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

267  { return _fe_map->get_dxyzdzeta(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dzetadx()

const std::vector<Real>& libMesh::FEAbstract::get_dzetadx ( ) const
inlineinherited
Returns
The dzeta/dx entry in the transformation matrix from physical to local coordinates.

Definition at line 359 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

360  { return this->_fe_map->get_dzetadx(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dzetady()

const std::vector<Real>& libMesh::FEAbstract::get_dzetady ( ) const
inlineinherited
Returns
The dzeta/dy entry in the transformation matrix from physical to local coordinates.

Definition at line 366 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

367  { return this->_fe_map->get_dzetady(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_dzetadz()

const std::vector<Real>& libMesh::FEAbstract::get_dzetadz ( ) const
inlineinherited
Returns
The dzeta/dz entry in the transformation matrix from physical to local coordinates.

Definition at line 373 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

374  { return this->_fe_map->get_dzetadz(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_family()

FEFamily libMesh::FEAbstract::get_family ( ) const
inlineinherited
Returns
The finite element family of this element.

Definition at line 455 of file fe_abstract.h.

References libMesh::FEType::family, and libMesh::FEAbstract::fe_type.

455 { return fe_type.family; }
libMesh::FEType::family
FEFamily family
Definition: fe_type.h:204

◆ get_fe_map()

const FEMap& libMesh::FEAbstract::get_fe_map ( ) const
inlineinherited
Returns
The mapping object

Definition at line 460 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

Referenced by libMesh::HCurlFETransformation< OutputShape >::init_map_d2phi(), libMesh::H1FETransformation< OutputShape >::init_map_d2phi(), libMesh::HCurlFETransformation< OutputShape >::init_map_dphi(), libMesh::H1FETransformation< OutputShape >::init_map_dphi(), libMesh::HCurlFETransformation< OutputShape >::init_map_phi(), libMesh::HCurlFETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_d2phi(), libMesh::H1FETransformation< OutputShape >::map_div(), libMesh::H1FETransformation< OutputShape >::map_dphi(), and libMesh::HCurlFETransformation< OutputShape >::map_phi().

460 { return *_fe_map.get(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_fe_type()

FEType libMesh::FEAbstract::get_fe_type ( ) const
inlineinherited
Returns
The FE Type (approximation order and family) of the finite element.

Definition at line 429 of file fe_abstract.h.

References libMesh::FEAbstract::fe_type.

Referenced by libMesh::FEMContext::build_new_fe(), libMesh::HCurlFETransformation< OutputShape >::map_phi(), libMesh::H1FETransformation< OutputShape >::map_phi(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), and libMesh::JumpErrorEstimator::reinit_sides().

429 { return fe_type; }

◆ get_info()

std::string libMesh::ReferenceCounter::get_info ( )
staticinherited

Gets a string containing the reference information.

Definition at line 47 of file reference_counter.C.

References libMesh::ReferenceCounter::_counts, and libMesh::Quality::name().

Referenced by libMesh::ReferenceCounter::print_info().

48 {
49 #if defined(LIBMESH_ENABLE_REFERENCE_COUNTING) && defined(DEBUG)
50 
51  std::ostringstream oss;
52 
53  oss << '\n'
54  << " ---------------------------------------------------------------------------- \n"
55  << "| Reference count information |\n"
56  << " ---------------------------------------------------------------------------- \n";
57 
58  for (const auto & pr : _counts)
59  {
60  const std::string name(pr.first);
61  const unsigned int creations = pr.second.first;
62  const unsigned int destructions = pr.second.second;
63 
64  oss << "| " << name << " reference count information:\n"
65  << "| Creations: " << creations << '\n'
66  << "| Destructions: " << destructions << '\n';
67  }
68 
69  oss << " ---------------------------------------------------------------------------- \n";
70 
71  return oss.str();
72 
73 #else
74 
75  return "";
76 
77 #endif
78 }
libMesh::Quality::name
std::string name(const ElemQuality q)
Definition: elem_quality.C:42

◆ get_JxW()

const std::vector<Real>& libMesh::FEAbstract::get_JxW ( ) const
inlineinherited
Returns
The element Jacobian times the quadrature weight for each quadrature point.

Definition at line 245 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::DiscontinuityMeasure::boundary_side_integration(), libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::System::calculate_norm(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::FEMSystem::init_context(), libMesh::LaplacianErrorEstimator::internal_side_integration(), libMesh::DiscontinuityMeasure::internal_side_integration(), libMesh::KellyErrorEstimator::internal_side_integration(), and libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()().

246  { return this->_fe_map->get_JxW(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_normals()

const std::vector<Point>& libMesh::FEAbstract::get_normals ( ) const
inlineinherited
Returns
The outward pointing normal vectors for face integration.

Definition at line 385 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

Referenced by libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::ParsedFEMFunction< T >::eval_args(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::KellyErrorEstimator::init_context(), and libMesh::KellyErrorEstimator::internal_side_integration().

386  { return this->_fe_map->get_normals(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_order()

Order libMesh::FEAbstract::get_order ( ) const
inlineinherited
Returns
The approximation order of the finite element.

Definition at line 434 of file fe_abstract.h.

References libMesh::FEAbstract::_p_level, libMesh::FEAbstract::fe_type, and libMesh::FEType::order.

434 { return static_cast<Order>(fe_type.order + _p_level); }
libMesh::FEAbstract::_p_level
unsigned int _p_level
Definition: fe_abstract.h:587
libMesh::FEType::order
OrderWrapper order
Definition: fe_type.h:198

◆ get_p_level()

unsigned int libMesh::FEAbstract::get_p_level ( ) const
inlineinherited
Returns
The p refinement level that the current shape functions have been calculated for.

Definition at line 424 of file fe_abstract.h.

References libMesh::FEAbstract::_p_level.

424 { return _p_level; }
libMesh::FEAbstract::_p_level
unsigned int _p_level
Definition: fe_abstract.h:587

◆ get_phi()

template<typename OutputType>
const std::vector<std::vector<OutputShape> >& libMesh::FEGenericBase< OutputType >::get_phi ( ) const
inlineinherited
Returns
The shape function values at the quadrature points on the element.

Definition at line 207 of file fe_base.h.

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::DiscontinuityMeasure::boundary_side_integration(), libMesh::System::calculate_norm(), libMesh::OldSolutionCoefs< Output, point_output >::eval_at_point(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::OldSolutionBase< Output, point_output >::get_shape_outputs(), libMesh::DiscontinuityMeasure::init_context(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::FEMSystem::init_context(), libMesh::FEMContext::interior_values(), libMesh::DiscontinuityMeasure::internal_side_integration(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), libMesh::FEMContext::side_values(), and libMesh::FEMContext::some_value().

208  { libmesh_assert(!calculations_started || calculate_phi);
209  calculate_phi = true; return phi; }
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498

◆ get_refspace_nodes()

void libMesh::FEAbstract::get_refspace_nodes ( const ElemType  t,
std::vector< Point > &  nodes 
)
staticinherited
Returns
The reference space coordinates of nodes based on the element type.

Definition at line 283 of file fe_abstract.C.

References libMesh::EDGE2, libMesh::EDGE3, libMesh::HEX20, libMesh::HEX27, libMesh::HEX8, libMesh::PRISM15, libMesh::PRISM18, libMesh::PRISM6, libMesh::PYRAMID13, libMesh::PYRAMID14, libMesh::PYRAMID5, libMesh::QUAD4, libMesh::QUAD8, libMesh::QUAD9, libMesh::QUADSHELL4, libMesh::QUADSHELL8, libMesh::TET10, libMesh::TET4, libMesh::TRI3, libMesh::TRI6, and libMesh::TRISHELL3.

284 {
285  switch(itemType)
286  {
287  case EDGE2:
288  {
289  nodes.resize(2);
290  nodes[0] = Point (-1.,0.,0.);
291  nodes[1] = Point (1.,0.,0.);
292  return;
293  }
294  case EDGE3:
295  {
296  nodes.resize(3);
297  nodes[0] = Point (-1.,0.,0.);
298  nodes[1] = Point (1.,0.,0.);
299  nodes[2] = Point (0.,0.,0.);
300  return;
301  }
302  case TRI3:
303  case TRISHELL3:
304  {
305  nodes.resize(3);
306  nodes[0] = Point (0.,0.,0.);
307  nodes[1] = Point (1.,0.,0.);
308  nodes[2] = Point (0.,1.,0.);
309  return;
310  }
311  case TRI6:
312  {
313  nodes.resize(6);
314  nodes[0] = Point (0.,0.,0.);
315  nodes[1] = Point (1.,0.,0.);
316  nodes[2] = Point (0.,1.,0.);
317  nodes[3] = Point (.5,0.,0.);
318  nodes[4] = Point (.5,.5,0.);
319  nodes[5] = Point (0.,.5,0.);
320  return;
321  }
322  case QUAD4:
323  case QUADSHELL4:
324  {
325  nodes.resize(4);
326  nodes[0] = Point (-1.,-1.,0.);
327  nodes[1] = Point (1.,-1.,0.);
328  nodes[2] = Point (1.,1.,0.);
329  nodes[3] = Point (-1.,1.,0.);
330  return;
331  }
332  case QUAD8:
333  case QUADSHELL8:
334  {
335  nodes.resize(8);
336  nodes[0] = Point (-1.,-1.,0.);
337  nodes[1] = Point (1.,-1.,0.);
338  nodes[2] = Point (1.,1.,0.);
339  nodes[3] = Point (-1.,1.,0.);
340  nodes[4] = Point (0.,-1.,0.);
341  nodes[5] = Point (1.,0.,0.);
342  nodes[6] = Point (0.,1.,0.);
343  nodes[7] = Point (-1.,0.,0.);
344  return;
345  }
346  case QUAD9:
347  {
348  nodes.resize(9);
349  nodes[0] = Point (-1.,-1.,0.);
350  nodes[1] = Point (1.,-1.,0.);
351  nodes[2] = Point (1.,1.,0.);
352  nodes[3] = Point (-1.,1.,0.);
353  nodes[4] = Point (0.,-1.,0.);
354  nodes[5] = Point (1.,0.,0.);
355  nodes[6] = Point (0.,1.,0.);
356  nodes[7] = Point (-1.,0.,0.);
357  nodes[8] = Point (0.,0.,0.);
358  return;
359  }
360  case TET4:
361  {
362  nodes.resize(4);
363  nodes[0] = Point (0.,0.,0.);
364  nodes[1] = Point (1.,0.,0.);
365  nodes[2] = Point (0.,1.,0.);
366  nodes[3] = Point (0.,0.,1.);
367  return;
368  }
369  case TET10:
370  {
371  nodes.resize(10);
372  nodes[0] = Point (0.,0.,0.);
373  nodes[1] = Point (1.,0.,0.);
374  nodes[2] = Point (0.,1.,0.);
375  nodes[3] = Point (0.,0.,1.);
376  nodes[4] = Point (.5,0.,0.);
377  nodes[5] = Point (.5,.5,0.);
378  nodes[6] = Point (0.,.5,0.);
379  nodes[7] = Point (0.,0.,.5);
380  nodes[8] = Point (.5,0.,.5);
381  nodes[9] = Point (0.,.5,.5);
382  return;
383  }
384  case HEX8:
385  {
386  nodes.resize(8);
387  nodes[0] = Point (-1.,-1.,-1.);
388  nodes[1] = Point (1.,-1.,-1.);
389  nodes[2] = Point (1.,1.,-1.);
390  nodes[3] = Point (-1.,1.,-1.);
391  nodes[4] = Point (-1.,-1.,1.);
392  nodes[5] = Point (1.,-1.,1.);
393  nodes[6] = Point (1.,1.,1.);
394  nodes[7] = Point (-1.,1.,1.);
395  return;
396  }
397  case HEX20:
398  {
399  nodes.resize(20);
400  nodes[0] = Point (-1.,-1.,-1.);
401  nodes[1] = Point (1.,-1.,-1.);
402  nodes[2] = Point (1.,1.,-1.);
403  nodes[3] = Point (-1.,1.,-1.);
404  nodes[4] = Point (-1.,-1.,1.);
405  nodes[5] = Point (1.,-1.,1.);
406  nodes[6] = Point (1.,1.,1.);
407  nodes[7] = Point (-1.,1.,1.);
408  nodes[8] = Point (0.,-1.,-1.);
409  nodes[9] = Point (1.,0.,-1.);
410  nodes[10] = Point (0.,1.,-1.);
411  nodes[11] = Point (-1.,0.,-1.);
412  nodes[12] = Point (-1.,-1.,0.);
413  nodes[13] = Point (1.,-1.,0.);
414  nodes[14] = Point (1.,1.,0.);
415  nodes[15] = Point (-1.,1.,0.);
416  nodes[16] = Point (0.,-1.,1.);
417  nodes[17] = Point (1.,0.,1.);
418  nodes[18] = Point (0.,1.,1.);
419  nodes[19] = Point (-1.,0.,1.);
420  return;
421  }
422  case HEX27:
423  {
424  nodes.resize(27);
425  nodes[0] = Point (-1.,-1.,-1.);
426  nodes[1] = Point (1.,-1.,-1.);
427  nodes[2] = Point (1.,1.,-1.);
428  nodes[3] = Point (-1.,1.,-1.);
429  nodes[4] = Point (-1.,-1.,1.);
430  nodes[5] = Point (1.,-1.,1.);
431  nodes[6] = Point (1.,1.,1.);
432  nodes[7] = Point (-1.,1.,1.);
433  nodes[8] = Point (0.,-1.,-1.);
434  nodes[9] = Point (1.,0.,-1.);
435  nodes[10] = Point (0.,1.,-1.);
436  nodes[11] = Point (-1.,0.,-1.);
437  nodes[12] = Point (-1.,-1.,0.);
438  nodes[13] = Point (1.,-1.,0.);
439  nodes[14] = Point (1.,1.,0.);
440  nodes[15] = Point (-1.,1.,0.);
441  nodes[16] = Point (0.,-1.,1.);
442  nodes[17] = Point (1.,0.,1.);
443  nodes[18] = Point (0.,1.,1.);
444  nodes[19] = Point (-1.,0.,1.);
445  nodes[20] = Point (0.,0.,-1.);
446  nodes[21] = Point (0.,-1.,0.);
447  nodes[22] = Point (1.,0.,0.);
448  nodes[23] = Point (0.,1.,0.);
449  nodes[24] = Point (-1.,0.,0.);
450  nodes[25] = Point (0.,0.,1.);
451  nodes[26] = Point (0.,0.,0.);
452  return;
453  }
454  case PRISM6:
455  {
456  nodes.resize(6);
457  nodes[0] = Point (0.,0.,-1.);
458  nodes[1] = Point (1.,0.,-1.);
459  nodes[2] = Point (0.,1.,-1.);
460  nodes[3] = Point (0.,0.,1.);
461  nodes[4] = Point (1.,0.,1.);
462  nodes[5] = Point (0.,1.,1.);
463  return;
464  }
465  case PRISM15:
466  {
467  nodes.resize(15);
468  nodes[0] = Point (0.,0.,-1.);
469  nodes[1] = Point (1.,0.,-1.);
470  nodes[2] = Point (0.,1.,-1.);
471  nodes[3] = Point (0.,0.,1.);
472  nodes[4] = Point (1.,0.,1.);
473  nodes[5] = Point (0.,1.,1.);
474  nodes[6] = Point (.5,0.,-1.);
475  nodes[7] = Point (.5,.5,-1.);
476  nodes[8] = Point (0.,.5,-1.);
477  nodes[9] = Point (0.,0.,0.);
478  nodes[10] = Point (1.,0.,0.);
479  nodes[11] = Point (0.,1.,0.);
480  nodes[12] = Point (.5,0.,1.);
481  nodes[13] = Point (.5,.5,1.);
482  nodes[14] = Point (0.,.5,1.);
483  return;
484  }
485  case PRISM18:
486  {
487  nodes.resize(18);
488  nodes[0] = Point (0.,0.,-1.);
489  nodes[1] = Point (1.,0.,-1.);
490  nodes[2] = Point (0.,1.,-1.);
491  nodes[3] = Point (0.,0.,1.);
492  nodes[4] = Point (1.,0.,1.);
493  nodes[5] = Point (0.,1.,1.);
494  nodes[6] = Point (.5,0.,-1.);
495  nodes[7] = Point (.5,.5,-1.);
496  nodes[8] = Point (0.,.5,-1.);
497  nodes[9] = Point (0.,0.,0.);
498  nodes[10] = Point (1.,0.,0.);
499  nodes[11] = Point (0.,1.,0.);
500  nodes[12] = Point (.5,0.,1.);
501  nodes[13] = Point (.5,.5,1.);
502  nodes[14] = Point (0.,.5,1.);
503  nodes[15] = Point (.5,0.,0.);
504  nodes[16] = Point (.5,.5,0.);
505  nodes[17] = Point (0.,.5,0.);
506  return;
507  }
508  case PYRAMID5:
509  {
510  nodes.resize(5);
511  nodes[0] = Point (-1.,-1.,0.);
512  nodes[1] = Point (1.,-1.,0.);
513  nodes[2] = Point (1.,1.,0.);
514  nodes[3] = Point (-1.,1.,0.);
515  nodes[4] = Point (0.,0.,1.);
516  return;
517  }
518  case PYRAMID13:
519  {
520  nodes.resize(13);
521 
522  // base corners
523  nodes[0] = Point (-1.,-1.,0.);
524  nodes[1] = Point (1.,-1.,0.);
525  nodes[2] = Point (1.,1.,0.);
526  nodes[3] = Point (-1.,1.,0.);
527 
528  // apex
529  nodes[4] = Point (0.,0.,1.);
530 
531  // base midedge
532  nodes[5] = Point (0.,-1.,0.);
533  nodes[6] = Point (1.,0.,0.);
534  nodes[7] = Point (0.,1.,0.);
535  nodes[8] = Point (-1,0.,0.);
536 
537  // lateral midedge
538  nodes[9] = Point (-.5,-.5,.5);
539  nodes[10] = Point (.5,-.5,.5);
540  nodes[11] = Point (.5,.5,.5);
541  nodes[12] = Point (-.5,.5,.5);
542 
543  return;
544  }
545  case PYRAMID14:
546  {
547  nodes.resize(14);
548 
549  // base corners
550  nodes[0] = Point (-1.,-1.,0.);
551  nodes[1] = Point (1.,-1.,0.);
552  nodes[2] = Point (1.,1.,0.);
553  nodes[3] = Point (-1.,1.,0.);
554 
555  // apex
556  nodes[4] = Point (0.,0.,1.);
557 
558  // base midedge
559  nodes[5] = Point (0.,-1.,0.);
560  nodes[6] = Point (1.,0.,0.);
561  nodes[7] = Point (0.,1.,0.);
562  nodes[8] = Point (-1,0.,0.);
563 
564  // lateral midedge
565  nodes[9] = Point (-.5,-.5,.5);
566  nodes[10] = Point (.5,-.5,.5);
567  nodes[11] = Point (.5,.5,.5);
568  nodes[12] = Point (-.5,.5,.5);
569 
570  // base center
571  nodes[13] = Point (0.,0.,0.);
572 
573  return;
574  }
575 
576  default:
577  libmesh_error_msg("ERROR: Unknown element type " << itemType);
578  }
579 }

◆ get_Sobolev_dweight()

template<typename OutputType>
const std::vector<RealGradient>& libMesh::FEGenericBase< OutputType >::get_Sobolev_dweight ( ) const
inlineinherited
Returns
The first global derivative of the multiplicative weight at each quadrature point. See get_Sobolev_weight() for details. In case of FE initialized to all zero.

Definition at line 427 of file fe_base.h.

428  { return dweight; }
libMesh::FEGenericBase::dweight
std::vector< RealGradient > dweight
Definition: fe_base.h:636

◆ get_Sobolev_weight()

template<typename OutputType>
const std::vector<Real>& libMesh::FEGenericBase< OutputType >::get_Sobolev_weight ( ) const
inlineinherited
Returns
The multiplicative weight at each quadrature point. This weight is used for certain infinite element weak formulations, so that weighted Sobolev spaces are used for the trial function space. This renders the variational form easily computable.

In case of the general finite element class FE this field is initialized to all ones, so that the variational formulation for an infinite element produces correct element matrices for a mesh using both finite and infinite elements.

Definition at line 419 of file fe_base.h.

420  { return weight; }
libMesh::FEGenericBase::weight
std::vector< Real > weight
Definition: fe_base.h:643

◆ get_tangents()

const std::vector<std::vector<Point> >& libMesh::FEAbstract::get_tangents ( ) const
inlineinherited
Returns
The tangent vectors for face integration.

Definition at line 379 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

380  { return this->_fe_map->get_tangents(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ get_type()

ElemType libMesh::FEAbstract::get_type ( ) const
inlineinherited
Returns
The element type that the current shape functions have been calculated for. Useful in determining when shape functions must be recomputed.

Definition at line 418 of file fe_abstract.h.

References libMesh::FEAbstract::elem_type.

418 { return elem_type; }

◆ get_xyz()

const std::vector<Point>& libMesh::FEAbstract::get_xyz ( ) const
inlineinherited
Returns
The xyz spatial locations of the quadrature points on the element.

Definition at line 238 of file fe_abstract.h.

References libMesh::FEAbstract::_fe_map.

Referenced by libMesh::ExactSolution::_compute_error(), libMesh::DiscontinuityMeasure::boundary_side_integration(), libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::JumpErrorEstimator::estimate_error(), libMesh::ParsedFEMFunction< T >::eval_args(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::DGFEMContext::neighbor_side_fe_reinit(), and libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()().

239  { return this->_fe_map->get_xyz(); }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ increment_constructor_count()

void libMesh::ReferenceCounter::increment_constructor_count ( const std::string &  name)
inlineprotectedinherited

Increments the construction counter. Should be called in the constructor of any derived class that will be reference counted.

Definition at line 181 of file reference_counter.h.

References libMesh::ReferenceCounter::_counts, libMesh::Quality::name(), and libMesh::Threads::spin_mtx.

Referenced by libMesh::ReferenceCountedObject< RBParametrized >::ReferenceCountedObject().

182 {
183  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
184  std::pair<unsigned int, unsigned int> & p = _counts[name];
185 
186  p.first++;
187 }
libMesh::Quality::name
std::string name(const ElemQuality q)
Definition: elem_quality.C:42
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29

◆ increment_destructor_count()

void libMesh::ReferenceCounter::increment_destructor_count ( const std::string &  name)
inlineprotectedinherited

Increments the destruction counter. Should be called in the destructor of any derived class that will be reference counted.

Definition at line 194 of file reference_counter.h.

References libMesh::ReferenceCounter::_counts, libMesh::Quality::name(), and libMesh::Threads::spin_mtx.

Referenced by libMesh::ReferenceCountedObject< RBParametrized >::~ReferenceCountedObject().

195 {
196  Threads::spin_mutex::scoped_lock lock(Threads::spin_mtx);
197  std::pair<unsigned int, unsigned int> & p = _counts[name];
198 
199  p.second++;
200 }
libMesh::Quality::name
std::string name(const ElemQuality q)
Definition: elem_quality.C:42
libMesh::Threads::spin_mtx
spin_mutex spin_mtx
Definition: threads.C:29

◆ init_base_shape_functions()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
virtual void libMesh::InfFE< Dim, T_radial, T_map >::init_base_shape_functions ( const std::vector< Point > &  ,
const Elem *   
)
inlineoverrideprotectedvirtual

Do not use this derived member in InfFE<Dim,T_radial,T_map>.

Implements libMesh::FEGenericBase< OutputType >.

Definition at line 518 of file inf_fe.h.

520  { libmesh_not_implemented(); }

◆ init_face_shape_functions()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_base>
void libMesh::InfFE< Dim, T_radial, T_base >::init_face_shape_functions ( const std::vector< Point > &  qp,
const Elem *  side 
)
protected

Not implemented yet. Initialize all the data fields like weight, phi, etc for the side s.

Definition at line 122 of file inf_fe_boundary.C.

References libMesh::FEGenericBase< OutputType >::build(), libMesh::Elem::p_level(), and libMesh::Elem::type().

124 {
125  libmesh_assert(inf_side);
126 
127  // Currently, this makes only sense in 3-D!
128  libmesh_assert_equal_to (Dim, 3);
129 
130  // Initialize the radial shape functions
131  this->init_radial_shape_functions(inf_side);
132 
133  // Initialize the base shape functions
134  this->update_base_elem(inf_side);
135 
136  // Initialize the base quadrature rule
137  base_qrule->init(base_elem->type(), inf_side->p_level());
138 
139  // base_fe still corresponds to the (dim-1)-dimensional base of the InfFE object,
140  // so update the fe_base.
141  {
142  libmesh_assert_equal_to (Dim, 3);
143  base_fe = FEBase::build(Dim-2, this->fe_type);
144  base_fe->attach_quadrature_rule(base_qrule.get());
145  }
146 
147  // initialize the shape functions on the base
148  base_fe->init_base_shape_functions(base_fe->qrule->get_points(),
149  base_elem.get());
150 
151  // the number of quadrature points
152  const unsigned int n_radial_qp =
153  cast_int<unsigned int>(som.size());
154  const unsigned int n_base_qp = base_qrule->n_points();
155  const unsigned int n_total_qp = n_radial_qp * n_base_qp;
156 
157  // the quadrature weights
158  _total_qrule_weights.resize(n_total_qp);
159 
160  // now init the shapes for boundary work
161  {
162 
163  // The element type and order to use in the base map
164  const Order base_mapping_order ( base_elem->default_order() );
165  const ElemType base_mapping_elem_type ( base_elem->type() );
166 
167  // the number of mapping shape functions
168  // (Lagrange shape functions are used for mapping in the base)
169  const unsigned int n_radial_mapping_sf =
170  cast_int<unsigned int>(radial_map.size());
171  const unsigned int n_base_mapping_shape_functions = Base::n_base_mapping_sf(base_mapping_elem_type,
172  base_mapping_order);
173 
174  const unsigned int n_total_mapping_shape_functions =
175  n_radial_mapping_sf * n_base_mapping_shape_functions;
176 
177 
178  // initialize the node and shape numbering maps
179  {
180  _radial_node_index.resize (n_total_mapping_shape_functions);
181  _base_node_index.resize (n_total_mapping_shape_functions);
182 
183  const ElemType inf_face_elem_type (inf_side->type());
184 
185  // fill the node index map
186  for (unsigned int n=0; n<n_total_mapping_shape_functions; n++)
187  {
188  compute_node_indices (inf_face_elem_type,
189  n,
190  _base_node_index[n],
191  _radial_node_index[n]);
192 
193  libmesh_assert_less (_base_node_index[n], n_base_mapping_shape_functions);
194  libmesh_assert_less (_radial_node_index[n], n_radial_mapping_sf);
195  }
196 
197  }
198 
199  // resize map data fields
200  {
201  std::vector<std::vector<Real>> & psi_map = this->_fe_map->get_psi();
202  std::vector<std::vector<Real>> & dpsidxi_map = this->_fe_map->get_dpsidxi();
203  std::vector<std::vector<Real>> & d2psidxi2_map = this->_fe_map->get_d2psidxi2();
204  psi_map.resize (n_total_mapping_shape_functions);
205  dpsidxi_map.resize (n_total_mapping_shape_functions);
206  d2psidxi2_map.resize (n_total_mapping_shape_functions);
207 
208  // if (Dim == 3)
209  {
210  std::vector<std::vector<Real>> & dpsideta_map = this->_fe_map->get_dpsideta();
211  std::vector<std::vector<Real>> & d2psidxideta_map = this->_fe_map->get_d2psidxideta();
212  std::vector<std::vector<Real>> & d2psideta2_map = this->_fe_map->get_d2psideta2();
213  dpsideta_map.resize (n_total_mapping_shape_functions);
214  d2psidxideta_map.resize (n_total_mapping_shape_functions);
215  d2psideta2_map.resize (n_total_mapping_shape_functions);
216  }
217 
218  for (unsigned int i=0; i<n_total_mapping_shape_functions; i++)
219  {
220  psi_map[i].resize (n_total_qp);
221  dpsidxi_map[i].resize (n_total_qp);
222  d2psidxi2_map[i].resize (n_total_qp);
223 
224  // if (Dim == 3)
225  {
226  std::vector<std::vector<Real>> & dpsideta_map = this->_fe_map->get_dpsideta();
227  std::vector<std::vector<Real>> & d2psidxideta_map = this->_fe_map->get_d2psidxideta();
228  std::vector<std::vector<Real>> & d2psideta2_map = this->_fe_map->get_d2psideta2();
229  dpsideta_map[i].resize (n_total_qp);
230  d2psidxideta_map[i].resize (n_total_qp);
231  d2psideta2_map[i].resize (n_total_qp);
232  }
233  }
234  }
235 
236 
237  // compute shape maps
238  {
239  const std::vector<std::vector<Real>> & S_map = (base_fe->get_fe_map()).get_phi_map();
240  const std::vector<std::vector<Real>> & Ss_map = (base_fe->get_fe_map()).get_dphidxi_map();
241 
242  std::vector<std::vector<Real>> & psi_map = this->_fe_map->get_psi();
243  std::vector<std::vector<Real>> & dpsidxi_map = this->_fe_map->get_dpsidxi();
244  std::vector<std::vector<Real>> & dpsideta_map = this->_fe_map->get_dpsideta();
245 
246  for (unsigned int rp=0; rp<n_radial_qp; rp++) // over radial qps
247  for (unsigned int bp=0; bp<n_base_qp; bp++) // over base qps
248  for (unsigned int ti=0; ti<n_total_mapping_shape_functions; ti++) // over all mapping shapes
249  {
250  // let the index vectors take care of selecting the appropriate base/radial mapping shape
251  const unsigned int bi = _base_node_index [ti];
252  const unsigned int ri = _radial_node_index[ti];
253  psi_map [ti][bp+rp*n_base_qp] = S_map [bi][bp] * radial_map [ri][rp];
254  dpsidxi_map [ti][bp+rp*n_base_qp] = Ss_map[bi][bp] * radial_map [ri][rp];
255  dpsideta_map [ti][bp+rp*n_base_qp] = S_map [bi][bp] * dradialdv_map[ri][rp];
256 
257  // second derivatives are not implemented for infinite elements
258  // d2psidxi2_map [ti][bp+rp*n_base_qp] = 0.;
259  // d2psidxideta_map [ti][bp+rp*n_base_qp] = 0.;
260  // d2psideta2_map [ti][bp+rp*n_base_qp] = 0.;
261  }
262 
263  }
264 
265  }
266 
267  // quadrature rule weights
268  {
269  const std::vector<Real> & radial_qw = radial_qrule->get_weights();
270  const std::vector<Real> & base_qw = base_qrule->get_weights();
271 
272  libmesh_assert_equal_to (radial_qw.size(), n_radial_qp);
273  libmesh_assert_equal_to (base_qw.size(), n_base_qp);
274 
275  for (unsigned int rp=0; rp<n_radial_qp; rp++)
276  for (unsigned int bp=0; bp<n_base_qp; bp++)
277  {
278  _total_qrule_weights[bp + rp*n_base_qp] = radial_qw[rp] * base_qw[bp];
279  }
280  }
281 
282 }
libMesh::InfFE::dradialdv_map
std::vector< std::vector< Real > > dradialdv_map
Definition: inf_fe.h:657
libMesh::InfFE::radial_map
std::vector< std::vector< Real > > radial_map
Definition: inf_fe.h:651
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::InfFE::_base_node_index
std::vector< unsigned int > _base_node_index
Definition: inf_fe.h:703
libMesh::InfFE::compute_node_indices
static void compute_node_indices(const ElemType inf_elem_type, const unsigned int outer_node_index, unsigned int &base_node, unsigned int &radial_node)
Definition: inf_fe_static.C:361
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764
libMesh::InfFE::Base::n_base_mapping_sf
static unsigned int n_base_mapping_sf(const ElemType base_elem_type, const Order base_mapping_order)
Definition: inf_fe_base_radial.C:98
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::FEGenericBase::build
static std::unique_ptr< FEGenericBase > build(const unsigned int dim, const FEType &type)
libMesh::InfFE::init_radial_shape_functions
void init_radial_shape_functions(const Elem *inf_elem, const std::vector< Point > *radial_pts=nullptr)
Definition: inf_fe.C:320
libMesh::InfFE::_radial_node_index
std::vector< unsigned int > _radial_node_index
Definition: inf_fe.h:693
libMesh::InfFE::som
std::vector< Real > som
Definition: inf_fe.h:629
libMesh::InfFE::base_qrule
std::unique_ptr< QBase > base_qrule
Definition: inf_fe.h:752
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525
libMesh::InfFE::_total_qrule_weights
std::vector< Real > _total_qrule_weights
Definition: inf_fe.h:746
libMesh::InfFE::update_base_elem
void update_base_elem(const Elem *inf_elem)
Definition: inf_fe.C:98

◆ init_radial_shape_functions()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::init_radial_shape_functions ( const Elem *  inf_elem,
const std::vector< Point > *  radial_pts = nullptr 
)
protected

Some of the member data only depend on the radial part of the infinite element. The parts that only change when the radial order changes, are initialized here.

Definition at line 320 of file inf_fe.C.

References libMesh::InfFE< Dim, T_radial, T_map >::eval(), and libMesh::InfFE< Dim, T_radial, T_map >::eval_deriv().

322 {
323  libmesh_assert(radial_qrule.get() || radial_pts);
324  libmesh_assert(inf_elem);
325 
326  // Start logging the radial shape function initialization
327  LOG_SCOPE("init_radial_shape_functions()", "InfFE");
328 
329  // initialize most of the things related to mapping
330 
331  // The order to use in the radial map (currently independent of the element type)
332  const Order radial_mapping_order = Radial::mapping_order();
333  const unsigned int n_radial_mapping_shape_functions = Radial::n_dofs(radial_mapping_order);
334 
335  // initialize most of the things related to physical approximation
336  const Order radial_approx_order = fe_type.radial_order;
337  const unsigned int n_radial_approx_shape_functions = Radial::n_dofs(radial_approx_order);
338 
339  const std::size_t n_radial_qp =
340  radial_pts ? radial_pts->size() : radial_qrule->n_points();
341  const std::vector<Point> & radial_qp =
342  radial_pts ? *radial_pts : radial_qrule->get_points();
343 
344  // resize the radial data fields
345 
346  // the radial polynomials (eval)
347  mode.resize (n_radial_approx_shape_functions);
348  dmodedv.resize (n_radial_approx_shape_functions);
349 
350  // the (1-v)/2 weight
351  som.resize (n_radial_qp);
352  dsomdv.resize (n_radial_qp);
353 
354  // the radial map
355  radial_map.resize (n_radial_mapping_shape_functions);
356  dradialdv_map.resize (n_radial_mapping_shape_functions);
357 
358 
359  for (unsigned int i=0; i<n_radial_mapping_shape_functions; i++)
360  {
361  radial_map[i].resize (n_radial_qp);
362  dradialdv_map[i].resize (n_radial_qp);
363  }
364 
365 
366  for (unsigned int i=0; i<n_radial_approx_shape_functions; i++)
367  {
368  mode[i].resize (n_radial_qp);
369  dmodedv[i].resize (n_radial_qp);
370  }
371 
372 
373  // compute scalar values at radial quadrature points
374  for (std::size_t p=0; p<n_radial_qp; p++)
375  {
376  som[p] = Radial::decay (radial_qp[p](0));
377  dsomdv[p] = Radial::decay_deriv (radial_qp[p](0));
378  }
379 
380 
381  // evaluate the mode shapes in radial direction at radial quadrature points
382  for (unsigned int i=0; i<n_radial_approx_shape_functions; i++)
383  for (std::size_t p=0; p<n_radial_qp; p++)
384  {
385  mode[i][p] = InfFE<Dim,T_radial,T_map>::eval (radial_qp[p](0), radial_approx_order, i);
386  dmodedv[i][p] = InfFE<Dim,T_radial,T_map>::eval_deriv (radial_qp[p](0), radial_approx_order, i);
387  }
388 
389 
390  // evaluate the mapping functions in radial direction at radial quadrature points
391  for (unsigned int i=0; i<n_radial_mapping_shape_functions; i++)
392  for (std::size_t p=0; p<n_radial_qp; p++)
393  {
394  radial_map[i][p] = InfFE<Dim,INFINITE_MAP,T_map>::eval (radial_qp[p](0), radial_mapping_order, i);
395  dradialdv_map[i][p] = InfFE<Dim,INFINITE_MAP,T_map>::eval_deriv (radial_qp[p](0), radial_mapping_order, i);
396  }
397 }
libMesh::InfFE::Radial::decay_deriv
static Real decay_deriv(const Real)
Definition: inf_fe.h:114
libMesh::InfFE::dsomdv
std::vector< Real > dsomdv
Definition: inf_fe.h:634
libMesh::InfFE::dradialdv_map
std::vector< std::vector< Real > > dradialdv_map
Definition: inf_fe.h:657
libMesh::InfFE::radial_map
std::vector< std::vector< Real > > radial_map
Definition: inf_fe.h:651
libMesh::InfFE::eval_deriv
static Real eval_deriv(Real v, Order o_radial, unsigned int i)
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::FEType::radial_order
OrderWrapper radial_order
Definition: fe_type.h:237
libMesh::InfFE::mode
std::vector< std::vector< Real > > mode
Definition: inf_fe.h:640
libMesh::InfFE::Radial::decay
static Real decay(const Real v)
Definition: inf_fe.h:827
libMesh::InfFE::eval
static Real eval(Real v, Order o_radial, unsigned int i)
libMesh::InfFE::Radial::n_dofs
static unsigned int n_dofs(const Order o_radial)
Definition: inf_fe.h:147
libMesh::InfFE::som
std::vector< Real > som
Definition: inf_fe.h:629
libMesh::InfFE::Radial::mapping_order
static Order mapping_order()
Definition: inf_fe.h:131
libMesh::InfFE::dmodedv
std::vector< std::vector< Real > > dmodedv
Definition: inf_fe.h:646

◆ init_shape_functions()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::init_shape_functions ( const std::vector< Point > &  radial_qp,
const std::vector< Point > &  base_qp,
const Elem *  inf_elem 
)
protected

Initialize all the data fields like weight, mode, phi, dphidxi, dphideta, dphidzeta, etc. for the current element. This method prepares the data related to the base part, and some of the combined fields.

Definition at line 404 of file inf_fe.C.

References libMesh::Elem::type(), and libMesh::MeshTools::weight().

407 {
408  libmesh_assert(inf_elem);
409 
410  // Start logging the radial shape function initialization
411  LOG_SCOPE("init_shape_functions()", "InfFE");
412 
413  // fast access to some const ints for the radial data
414  const unsigned int n_radial_mapping_sf = cast_int<unsigned int>(radial_map.size());
415  const unsigned int n_radial_approx_sf = cast_int<unsigned int>(mode.size());
416  const unsigned int n_radial_qp = cast_int<unsigned int>(som.size());
417 
418 
419  // initialize most of the things related to mapping
420 
421  // The element type and order to use in the base map
422  const Order base_mapping_order = base_elem->default_order();
423  const ElemType base_mapping_elem_type = base_elem->type();
424 
425  // the number of base shape functions used to construct the map
426  // (Lagrange shape functions are used for mapping in the base)
427  unsigned int n_base_mapping_shape_functions = Base::n_base_mapping_sf(base_mapping_elem_type,
428  base_mapping_order);
429 
430  const unsigned int n_total_mapping_shape_functions =
431  n_radial_mapping_sf * n_base_mapping_shape_functions;
432 
433  // initialize most of the things related to physical approximation
434  unsigned int n_base_approx_shape_functions;
435  if (Dim > 1)
436  n_base_approx_shape_functions = base_fe->n_shape_functions();
437  else
438  n_base_approx_shape_functions = 1;
439 
440 
441  const unsigned int n_total_approx_shape_functions =
442  n_radial_approx_sf * n_base_approx_shape_functions;
443 
444  // update class member field
445  _n_total_approx_sf = n_total_approx_shape_functions;
446 
447 
448  // The number of the base quadrature points.
449  const unsigned int n_base_qp = cast_int<unsigned int>(base_qp.size());
450 
451  // The total number of quadrature points.
452  const unsigned int n_total_qp = n_radial_qp * n_base_qp;
453 
454 
455  // update class member field
456  _n_total_qp = n_total_qp;
457 
458 
459 
460  // initialize the node and shape numbering maps
461  {
462  // these vectors work as follows: the i-th entry stores
463  // the associated base/radial node number
464  _radial_node_index.resize(n_total_mapping_shape_functions);
465  _base_node_index.resize(n_total_mapping_shape_functions);
466 
467  // similar for the shapes: the i-th entry stores
468  // the associated base/radial shape number
469  _radial_shape_index.resize(n_total_approx_shape_functions);
470  _base_shape_index.resize(n_total_approx_shape_functions);
471 
472  const ElemType inf_elem_type = inf_elem->type();
473 
474  // fill the node index map
475  for (unsigned int n=0; n<n_total_mapping_shape_functions; n++)
476  {
477  compute_node_indices (inf_elem_type,
478  n,
479  _base_node_index[n],
480  _radial_node_index[n]);
481  libmesh_assert_less (_base_node_index[n], n_base_mapping_shape_functions);
482  libmesh_assert_less (_radial_node_index[n], n_radial_mapping_sf);
483  }
484 
485  // fill the shape index map
486  for (unsigned int n=0; n<n_total_approx_shape_functions; n++)
487  {
488  compute_shape_indices (this->fe_type,
489  inf_elem_type,
490  n,
491  _base_shape_index[n],
492  _radial_shape_index[n]);
493  libmesh_assert_less (_base_shape_index[n], n_base_approx_shape_functions);
494  libmesh_assert_less (_radial_shape_index[n], n_radial_approx_sf);
495  }
496  }
497 
498  // resize the base data fields
499  dist.resize(n_base_mapping_shape_functions);
500 
501  // resize the total data fields
502 
503  // the phase term varies with xi, eta and zeta(v): store it for _all_ qp
504  //
505  // when computing the phase, we need the base approximations
506  // therefore, initialize the phase here, but evaluate it
507  // in combine_base_radial().
508  //
509  // the weight, though, is only needed at the radial quadrature points, n_radial_qp.
510  // but for a uniform interface to the protected data fields
511  // the weight data field (which are accessible from the outside) are expanded to n_total_qp.
512  weight.resize (n_total_qp);
513  dweightdv.resize (n_total_qp);
514  dweight.resize (n_total_qp);
515 
516  dphase.resize (n_total_qp);
517  dphasedxi.resize (n_total_qp);
518  dphasedeta.resize (n_total_qp);
519  dphasedzeta.resize (n_total_qp);
520 
521  // this vector contains the integration weights for the combined quadrature rule
522  _total_qrule_weights.resize(n_total_qp);
523 
524  // InfFE's data fields phi, dphi, dphidx, phi_map etc hold the _total_
525  // shape and mapping functions, respectively
526  {
527  phi.resize (n_total_approx_shape_functions);
528  dphi.resize (n_total_approx_shape_functions);
529  dphidx.resize (n_total_approx_shape_functions);
530  dphidy.resize (n_total_approx_shape_functions);
531  dphidz.resize (n_total_approx_shape_functions);
532  dphidxi.resize (n_total_approx_shape_functions);
533 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
534  libmesh_warning("Warning: Second derivatives for Infinite elements"
535  << " are not yet implemented!"
536  << std::endl);
537 
538  d2phi.resize (n_total_approx_shape_functions);
539  d2phidx2.resize (n_total_approx_shape_functions);
540  d2phidxdy.resize (n_total_approx_shape_functions);
541  d2phidxdz.resize (n_total_approx_shape_functions);
542  d2phidy2.resize (n_total_approx_shape_functions);
543  d2phidydz.resize (n_total_approx_shape_functions);
544  d2phidz2.resize (n_total_approx_shape_functions);
545  d2phidxi2.resize (n_total_approx_shape_functions);
546 
547  if (Dim > 1)
548  {
549  d2phidxideta.resize(n_total_approx_shape_functions);
550  d2phideta2.resize(n_total_approx_shape_functions);
551  }
552 
553  if (Dim > 2)
554  {
555  d2phidetadzeta.resize(n_total_approx_shape_functions);
556  d2phidxidzeta.resize(n_total_approx_shape_functions);
557  d2phidzeta2.resize(n_total_approx_shape_functions);
558  }
559 #endif // ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
560 
561  if (Dim > 1)
562  dphideta.resize(n_total_approx_shape_functions);
563 
564  if (Dim == 3)
565  dphidzeta.resize(n_total_approx_shape_functions);
566 
567  std::vector<std::vector<Real>> & phi_map = this->_fe_map->get_phi_map();
568  std::vector<std::vector<Real>> & dphidxi_map = this->_fe_map->get_dphidxi_map();
569 
570  phi_map.resize(n_total_mapping_shape_functions);
571  dphidxi_map.resize(n_total_mapping_shape_functions);
572 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
573  std::vector<std::vector<Real>> & d2phidxi2_map = this->_fe_map->get_d2phidxi2_map();
574  d2phidxi2_map.resize(n_total_mapping_shape_functions);
575 
576  if (Dim > 1)
577  {
578  std::vector<std::vector<Real>> & d2phidxideta_map = this->_fe_map->get_d2phidxideta_map();
579  std::vector<std::vector<Real>> & d2phideta2_map = this->_fe_map->get_d2phideta2_map();
580  d2phidxideta_map.resize(n_total_mapping_shape_functions);
581  d2phideta2_map.resize(n_total_mapping_shape_functions);
582  }
583 
584  if (Dim == 3)
585  {
586  std::vector<std::vector<Real>> & d2phidxidzeta_map = this->_fe_map->get_d2phidxidzeta_map();
587  std::vector<std::vector<Real>> & d2phidetadzeta_map = this->_fe_map->get_d2phidetadzeta_map();
588  std::vector<std::vector<Real>> & d2phidzeta2_map = this->_fe_map->get_d2phidzeta2_map();
589  d2phidxidzeta_map.resize(n_total_mapping_shape_functions);
590  d2phidetadzeta_map.resize(n_total_mapping_shape_functions);
591  d2phidzeta2_map.resize(n_total_mapping_shape_functions);
592  }
593 #endif // ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
594 
595  if (Dim > 1)
596  {
597  std::vector<std::vector<Real>> & dphideta_map = this->_fe_map->get_dphideta_map();
598  dphideta_map.resize(n_total_mapping_shape_functions);
599  }
600 
601  if (Dim == 3)
602  {
603  std::vector<std::vector<Real>> & dphidzeta_map = this->_fe_map->get_dphidzeta_map();
604  dphidzeta_map.resize(n_total_mapping_shape_functions);
605  }
606  }
607 
608  // collect all the for loops, where inner vectors are
609  // resized to the appropriate number of quadrature points
610  {
611  for (unsigned int i=0; i<n_total_approx_shape_functions; i++)
612  {
613  phi[i].resize (n_total_qp);
614  dphi[i].resize (n_total_qp);
615  dphidx[i].resize (n_total_qp);
616  dphidy[i].resize (n_total_qp);
617  dphidz[i].resize (n_total_qp);
618  dphidxi[i].resize (n_total_qp);
619 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
620  d2phi[i].resize (n_total_qp);
621  d2phidx2[i].resize (n_total_qp);
622  d2phidxdy[i].resize (n_total_qp);
623  d2phidxdz[i].resize (n_total_qp);
624  d2phidy2[i].resize (n_total_qp);
625  d2phidydz[i].resize (n_total_qp);
626  d2phidy2[i].resize (n_total_qp);
627  d2phidxi2[i].resize (n_total_qp);
628 
629  if (Dim > 1)
630  {
631  d2phidxideta[i].resize (n_total_qp);
632  d2phideta2[i].resize (n_total_qp);
633  }
634  if (Dim > 2)
635  {
636  d2phidxidzeta[i].resize (n_total_qp);
637  d2phidetadzeta[i].resize (n_total_qp);
638  d2phidzeta2[i].resize (n_total_qp);
639  }
640 #endif // ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
641 
642  if (Dim > 1)
643  dphideta[i].resize (n_total_qp);
644 
645  if (Dim == 3)
646  dphidzeta[i].resize (n_total_qp);
647 
648  }
649 
650  for (unsigned int i=0; i<n_total_mapping_shape_functions; i++)
651  {
652  std::vector<std::vector<Real>> & phi_map = this->_fe_map->get_phi_map();
653  std::vector<std::vector<Real>> & dphidxi_map = this->_fe_map->get_dphidxi_map();
654  phi_map[i].resize (n_total_qp);
655  dphidxi_map[i].resize (n_total_qp);
656 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
657  std::vector<std::vector<Real>> & d2phidxi2_map = this->_fe_map->get_d2phidxi2_map();
658  d2phidxi2_map[i].resize (n_total_qp);
659  if (Dim > 1)
660  {
661  std::vector<std::vector<Real>> & d2phidxideta_map = this->_fe_map->get_d2phidxideta_map();
662  std::vector<std::vector<Real>> & d2phideta2_map = this->_fe_map->get_d2phideta2_map();
663  d2phidxideta_map[i].resize (n_total_qp);
664  d2phideta2_map[i].resize (n_total_qp);
665  }
666 
667  if (Dim > 2)
668  {
669  std::vector<std::vector<Real>> & d2phidxidzeta_map = this->_fe_map->get_d2phidxidzeta_map();
670  std::vector<std::vector<Real>> & d2phidetadzeta_map = this->_fe_map->get_d2phidetadzeta_map();
671  std::vector<std::vector<Real>> & d2phidzeta2_map = this->_fe_map->get_d2phidzeta2_map();
672  d2phidxidzeta_map[i].resize (n_total_qp);
673  d2phidetadzeta_map[i].resize (n_total_qp);
674  d2phidzeta2_map[i].resize (n_total_qp);
675  }
676 #endif // ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
677 
678  if (Dim > 1)
679  {
680  std::vector<std::vector<Real>> & dphideta_map = this->_fe_map->get_dphideta_map();
681  dphideta_map[i].resize (n_total_qp);
682  }
683 
684  if (Dim == 3)
685  {
686  std::vector<std::vector<Real>> & dphidzeta_map = this->_fe_map->get_dphidzeta_map();
687  dphidzeta_map[i].resize (n_total_qp);
688  }
689  }
690  }
691 
692 
693 
694  {
695  // (a) compute scalar values at _all_ quadrature points -- for uniform
696  // access from the outside to these fields
697  // (b) form a std::vector<Real> which contains the appropriate weights
698  // of the combined quadrature rule!
699  libmesh_assert_equal_to (radial_qp.size(), n_radial_qp);
700 
701  if (radial_qrule && base_qrule)
702  {
703  const std::vector<Real> & radial_qw = radial_qrule->get_weights();
704  const std::vector<Real> & base_qw = base_qrule->get_weights();
705  libmesh_assert_equal_to (radial_qw.size(), n_radial_qp);
706  libmesh_assert_equal_to (base_qw.size(), n_base_qp);
707 
708  for (unsigned int rp=0; rp<n_radial_qp; rp++)
709  for (unsigned int bp=0; bp<n_base_qp; bp++)
710  {
711  weight[bp + rp*n_base_qp] = Radial::D(radial_qp[rp](0));
712  dweightdv[bp + rp*n_base_qp] = Radial::D_deriv(radial_qp[rp](0));
713  _total_qrule_weights[bp + rp*n_base_qp] = radial_qw[rp] * base_qw[bp];
714  }
715  }
716  else
717  {
718  for (unsigned int rp=0; rp<n_radial_qp; rp++)
719  for (unsigned int bp=0; bp<n_base_qp; bp++)
720  {
721  weight[bp + rp*n_base_qp] = Radial::D(radial_qp[rp](0));
722  dweightdv[bp + rp*n_base_qp] = Radial::D_deriv(radial_qp[rp](0));
723  }
724  }
725  }
726 }
libMesh::FEGenericBase::d2phi
std::vector< std::vector< OutputTensor > > d2phi
Definition: fe_base.h:551
libMesh::FEGenericBase::dphidxi
std::vector< std::vector< OutputShape > > dphidxi
Definition: fe_base.h:518
libMesh::FEGenericBase::d2phidxdz
std::vector< std::vector< OutputShape > > d2phidxdz
Definition: fe_base.h:596
libMesh::FEGenericBase::dphidzeta
std::vector< std::vector< OutputShape > > dphidzeta
Definition: fe_base.h:528
libMesh::FEGenericBase::d2phidydz
std::vector< std::vector< OutputShape > > d2phidydz
Definition: fe_base.h:606
libMesh::InfFE::radial_map
std::vector< std::vector< Real > > radial_map
Definition: inf_fe.h:651
libMesh::InfFE::Radial::D
static Real D(const Real v)
Definition: inf_fe.h:120
libMesh::InfFE::dphasedxi
std::vector< Real > dphasedxi
Definition: inf_fe.h:664
libMesh::InfFE::dweightdv
std::vector< Real > dweightdv
Definition: inf_fe.h:620
libMesh::FEGenericBase::d2phidxideta
std::vector< std::vector< OutputShape > > d2phidxideta
Definition: fe_base.h:561
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::InfFE::_base_node_index
std::vector< unsigned int > _base_node_index
Definition: inf_fe.h:703
libMesh::InfFE::_n_total_qp
unsigned int _n_total_qp
Definition: inf_fe.h:740
libMesh::FEGenericBase::weight
std::vector< Real > weight
Definition: fe_base.h:643
libMesh::FEGenericBase::d2phidx2
std::vector< std::vector< OutputShape > > d2phidx2
Definition: fe_base.h:586
libMesh::InfFE::compute_node_indices
static void compute_node_indices(const ElemType inf_elem_type, const unsigned int outer_node_index, unsigned int &base_node, unsigned int &radial_node)
Definition: inf_fe_static.C:361
libMesh::FEGenericBase::dphidy
std::vector< std::vector< OutputShape > > dphidy
Definition: fe_base.h:538
libMesh::FEGenericBase::d2phidy2
std::vector< std::vector< OutputShape > > d2phidy2
Definition: fe_base.h:601
libMesh::InfFE::mode
std::vector< std::vector< Real > > mode
Definition: inf_fe.h:640
libMesh::FEGenericBase::d2phidetadzeta
std::vector< std::vector< OutputShape > > d2phidetadzeta
Definition: fe_base.h:576
libMesh::FEGenericBase::d2phidxidzeta
std::vector< std::vector< OutputShape > > d2phidxidzeta
Definition: fe_base.h:566
libMesh::FEGenericBase::d2phidxdy
std::vector< std::vector< OutputShape > > d2phidxdy
Definition: fe_base.h:591
libMesh::FEGenericBase::dphidx
std::vector< std::vector< OutputShape > > dphidx
Definition: fe_base.h:533
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498
libMesh::FEGenericBase::d2phideta2
std::vector< std::vector< OutputShape > > d2phideta2
Definition: fe_base.h:571
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764
libMesh::InfFE::Base::n_base_mapping_sf
static unsigned int n_base_mapping_sf(const ElemType base_elem_type, const Order base_mapping_order)
Definition: inf_fe_base_radial.C:98
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::FEGenericBase::dphase
std::vector< OutputGradient > dphase
Definition: fe_base.h:629
libMesh::InfFE::dphasedzeta
std::vector< Real > dphasedzeta
Definition: inf_fe.h:678
libMesh::InfFE::dphasedeta
std::vector< Real > dphasedeta
Definition: inf_fe.h:671
libMesh::InfFE::Radial::D_deriv
static Real D_deriv(const Real v)
Definition: inf_fe.h:125
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503
libMesh::InfFE::_n_total_approx_sf
unsigned int _n_total_approx_sf
Definition: inf_fe.h:734
libMesh::InfFE::_radial_node_index
std::vector< unsigned int > _radial_node_index
Definition: inf_fe.h:693
libMesh::InfFE::som
std::vector< Real > som
Definition: inf_fe.h:629
libMesh::InfFE::base_qrule
std::unique_ptr< QBase > base_qrule
Definition: inf_fe.h:752
libMesh::InfFE::compute_shape_indices
static void compute_shape_indices(const FEType &fet, const ElemType inf_elem_type, const unsigned int i, unsigned int &base_shape, unsigned int &radial_shape)
Definition: inf_fe_static.C:677
libMesh::InfFE::_radial_shape_index
std::vector< unsigned int > _radial_shape_index
Definition: inf_fe.h:713
libMesh::FEGenericBase::d2phidz2
std::vector< std::vector< OutputShape > > d2phidz2
Definition: fe_base.h:611
libMesh::FEGenericBase::d2phidxi2
std::vector< std::vector< OutputShape > > d2phidxi2
Definition: fe_base.h:556
libMesh::InfFE::_base_shape_index
std::vector< unsigned int > _base_shape_index
Definition: inf_fe.h:723
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525
libMesh::InfFE::dist
std::vector< Real > dist
Definition: inf_fe.h:612
libMesh::InfFE::_total_qrule_weights
std::vector< Real > _total_qrule_weights
Definition: inf_fe.h:746
libMesh::FEGenericBase::d2phidzeta2
std::vector< std::vector< OutputShape > > d2phidzeta2
Definition: fe_base.h:581
libMesh::FEGenericBase::dphidz
std::vector< std::vector< OutputShape > > dphidz
Definition: fe_base.h:543
libMesh::FEGenericBase::dphideta
std::vector< std::vector< OutputShape > > dphideta
Definition: fe_base.h:523
libMesh::FEGenericBase::dweight
std::vector< RealGradient > dweight
Definition: fe_base.h:636

◆ inverse_map() [1/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
Point libMesh::InfFE< Dim, T_radial, T_map >::inverse_map ( const Elem *  elem,
const Point &  p,
const Real  tolerance = TOLERANCE,
const bool  secure = true 
)
static
Returns
The location (on the reference element) of the point p located in physical space. First, the location in the base face is computed. This requires inverting the (possibly nonlinear) transformation map in the base, so it is not trivial. The optional parameter tolerance defines how close is "good enough." The map inversion iteration computes the sequence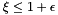 $ \{ p_n \} $, and the iteration is terminated when 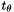$ \|p - p_n\| < \mbox{\texttt{tolerance}} $. Once the base face point is determined, the radial local coordinate is directly evaluated. If interpolated is true, the interpolated distance from the base element to the infinite element origin is used for the map in radial direction.

Definition at line 90 of file inf_fe_map.C.

References libMesh::TypeVector< T >::add_scaled(), libMesh::CARTESIAN, libMesh::FE< Dim, T >::inverse_map(), libMesh::libmesh_isinf(), libMesh::InfFE< Dim, T_radial, T_map >::map(), libMesh::TypeVector< T >::norm(), libMesh::Elem::origin(), and libMesh::Real.

Referenced by libMesh::FEInterface::ifem_inverse_map().

94 {
95  libmesh_assert(inf_elem);
96  libmesh_assert_greater_equal (tolerance, 0.);
97 
98  // Start logging the map inversion.
99  LOG_SCOPE("inverse_map()", "InfFE");
100 
101  // The strategy is:
102  // compute the intersection of the line
103  // physical_point - origin with the base element,
104  // find its internal coordinatels using FE<Dim-1,LAGRANGE>::inverse_map():
105  // The radial part can then be computed directly later on.
106 
107  // 1.)
108  // build a base element to do the map inversion in the base face
109  std::unique_ptr<Elem> base_elem (Base::build_elem (inf_elem));
110 
111  // The point on the reference element (which we are looking for).
112  Point p;
113 
114  // 2.)
115  // Now find the intersection of a plane represented by the base
116  // element nodes and the line given by the origin of the infinite
117  // element and the physical point.
118  Point intersection;
119 
120  // the origin of the infinite element
121  const Point o = inf_elem->origin();
122 
123  switch (Dim)
124  {
125  // unnecessary for 1D
126  case 1:
127  break;
128 
129  case 2:
130  libmesh_error_msg("ERROR: InfFE::inverse_map is not yet implemented in 2d");
131 
132  case 3:
133  {
134  // references to the nodal points of the base element
135  const Point & p0 = base_elem->point(0);
136  const Point & p1 = base_elem->point(1);
137  const Point & p2 = base_elem->point(2);
138 
139  // a reference to the physical point
140  const Point & fp = physical_point;
141 
142  // The intersection of the plane and the line is given by
143  // can be computed solving a linear 3x3 system
144  // a*({p1}-{p0})+b*({p2}-{p0})-c*({fp}-{o})={fp}-{p0}.
145  const Real c_factor = -(p1(0)*fp(1)*p0(2)-p1(0)*fp(2)*p0(1)
146  +fp(0)*p1(2)*p0(1)-p0(0)*fp(1)*p1(2)
147  +p0(0)*fp(2)*p1(1)+p2(0)*fp(2)*p0(1)
148  -p2(0)*fp(1)*p0(2)-fp(0)*p2(2)*p0(1)
149  +fp(0)*p0(2)*p2(1)+p0(0)*fp(1)*p2(2)
150  -p0(0)*fp(2)*p2(1)-fp(0)*p0(2)*p1(1)
151  +p0(2)*p2(0)*p1(1)-p0(1)*p2(0)*p1(2)
152  -fp(0)*p1(2)*p2(1)+p2(1)*p0(0)*p1(2)
153  -p2(0)*fp(2)*p1(1)-p1(0)*fp(1)*p2(2)
154  +p2(2)*p1(0)*p0(1)+p1(0)*fp(2)*p2(1)
155  -p0(2)*p1(0)*p2(1)-p2(2)*p0(0)*p1(1)
156  +fp(0)*p2(2)*p1(1)+p2(0)*fp(1)*p1(2))/
157  (fp(0)*p1(2)*p0(1)-p1(0)*fp(2)*p0(1)
158  +p1(0)*fp(1)*p0(2)-p1(0)*o(1)*p0(2)
159  +o(0)*p2(2)*p0(1)-p0(0)*fp(2)*p2(1)
160  +p1(0)*o(1)*p2(2)+fp(0)*p0(2)*p2(1)
161  -fp(0)*p1(2)*p2(1)-p0(0)*o(1)*p2(2)
162  +p0(0)*fp(1)*p2(2)-o(0)*p0(2)*p2(1)
163  +o(0)*p1(2)*p2(1)-p2(0)*fp(2)*p1(1)
164  +fp(0)*p2(2)*p1(1)-p2(0)*fp(1)*p0(2)
165  -o(2)*p0(0)*p1(1)-fp(0)*p0(2)*p1(1)
166  +p0(0)*o(1)*p1(2)+p0(0)*fp(2)*p1(1)
167  -p0(0)*fp(1)*p1(2)-o(0)*p1(2)*p0(1)
168  -p2(0)*o(1)*p1(2)-o(2)*p2(0)*p0(1)
169  -o(2)*p1(0)*p2(1)+o(2)*p0(0)*p2(1)
170  -fp(0)*p2(2)*p0(1)+o(2)*p2(0)*p1(1)
171  +p2(0)*o(1)*p0(2)+p2(0)*fp(1)*p1(2)
172  +p2(0)*fp(2)*p0(1)-p1(0)*fp(1)*p2(2)
173  +p1(0)*fp(2)*p2(1)-o(0)*p2(2)*p1(1)
174  +o(2)*p1(0)*p0(1)+o(0)*p0(2)*p1(1));
175 
176 
177  // Check whether the above system is ill-posed. It should
178  // only happen when \p physical_point is not in \p
179  // inf_elem. In this case, any point that is not in the
180  // element is a valid answer.
181  if (libmesh_isinf(c_factor))
182  return o;
183 
184  // The intersection should always be between the origin and the physical point.
185  // It can become positive close to the border, but should
186  // be only very small.
187  // So as in the case above, we can be sufficiently sure here
188  // that \p fp is not in this element:
189  if (c_factor > 0.01)
190  return o;
191 
192  // Compute the intersection with
193  // {intersection} = {fp} + c*({fp}-{o}).
194  intersection.add_scaled(fp,1.+c_factor);
195  intersection.add_scaled(o,-c_factor);
196 
197  break;
198  }
199 
200  default:
201  libmesh_error_msg("Invalid dim = " << Dim);
202  }
203 
204  // 3.)
205  // Now we have the intersection-point (projection of physical point onto base-element).
206  // Lets compute its internal coordinates (being p(0) and p(1)):
207  p= FE<Dim-1,LAGRANGE>::inverse_map(base_elem.get(), intersection, tolerance, secure);
208 
209  // 4.
210  //
211  // Now that we have the local coordinates in the base,
212  // we compute the radial distance with Newton iteration.
213 
214  // distance from the physical point to the ifem origin
215  const Real fp_o_dist = Point(o-physical_point).norm();
216 
217  // the distance from the intersection on the
218  // base to the origin
219  const Real a_dist = Point(o-intersection).norm();
220 
221  // element coordinate in radial direction
222  Real v = 0;
223 
224  // Physical_point is not in this element (return the best approximation)
225  if (fp_o_dist < a_dist)
226  {
227  v=-1;
228  }
229 
230  // fp_o_dist is at infinity.
231  if (libmesh_isinf(fp_o_dist))
232  {
233  v=1;
234  }
235 
236  // when we are somewhere in this element:
237  if (v==0)
238  {
239  // We know the analytic answer for CARTESIAN,
240  // other schemes do not yet have a better guess.
241  if (T_map == CARTESIAN)
242  v = 1.-2.*a_dist/fp_o_dist;
243  else
244  libmesh_not_implemented();
245 
246  // after the tests above, this should never be reached,
247  // but lets be safe and ensure a valid result.
248  if (v <= -1.-1e-5)
249  v=-1.;
250  if (v >= 1.)
251  v=1.-1e-5;
252  }
253 
254  p(Dim-1)=v;
255 #ifdef DEBUG
256  const Point check = InfFE<Dim,T_radial,T_map>::map (inf_elem, p);
257  const Point diff = physical_point - check;
258 
259  if (diff.norm() > tolerance)
260  libmesh_warning("WARNING: diff is " << diff.norm());
261 #endif
262 
263  return p;
264 }
libMesh::InfFE::Base::build_elem
static Elem * build_elem(const Elem *inf_elem)
Definition: inf_fe_base_radial.C:36
libMesh::libmesh_isinf
bool libmesh_isinf(T x)
Definition: libmesh_common.h:182
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::InfFE::map
static Point map(const Elem *inf_elem, const Point &reference_point)
Definition: inf_fe_map.C:40
libMesh::FE::inverse_map
static Point inverse_map(const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: fe_map.C:1576

◆ inverse_map() [2/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::inverse_map ( const Elem *  elem,
const std::vector< Point > &  physical_points,
std::vector< Point > &  reference_points,
const Real  tolerance = TOLERANCE,
const bool  secure = true 
)
static

Takes a number points in physical space (in the physical_points vector) and finds their location on the reference element for the input element elem. The values on the reference element are returned in the vector reference_points

Definition at line 269 of file inf_fe_map.C.

References libMesh::TypeVector< T >::size().

274 {
275  // The number of points to find the
276  // inverse map of
277  const std::size_t n_points = physical_points.size();
278 
279  // Resize the vector to hold the points
280  // on the reference element
281  reference_points.resize(n_points);
282 
283  // Find the coordinates on the reference
284  // element of each point in physical space
285  for (unsigned int p=0; p<n_points; p++)
286  reference_points[p] =
287  InfFE<Dim,T_radial,T_map>::inverse_map (elem, physical_points[p], tolerance, secure);
288 }
libMesh::InfFE::inverse_map
static Point inverse_map(const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: inf_fe_map.C:90

◆ is_hierarchic()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
virtual bool libMesh::InfFE< Dim, T_radial, T_map >::is_hierarchic ( ) const
inlineoverridevirtual
Returns
true if the element's higher order shape functions are hierarchic

Implements libMesh::FEAbstract.

Definition at line 339 of file inf_fe.h.

340  { return false; } // FIXME - Inf FEs don't handle p elevation yet

◆ map()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
Point libMesh::InfFE< Dim, T_radial, T_map >::map ( const Elem *  inf_elem,
const Point &  reference_point 
)
static
Returns
The location (in physical space) of the point p located on the reference element.

Definition at line 40 of file inf_fe_map.C.

References libMesh::TypeVector< T >::add_scaled(), libMesh::FE< Dim, T >::map(), libMesh::Elem::origin(), libMesh::Elem::point(), and libMesh::Real.

Referenced by libMesh::FEInterface::ifem_map(), and libMesh::InfFE< Dim, T_radial, T_map >::inverse_map().

42 {
43  libmesh_assert(inf_elem);
44  libmesh_assert_not_equal_to (Dim, 0);
45 
46  std::unique_ptr<Elem> base_elem (Base::build_elem (inf_elem));
47 
48  const Order radial_mapping_order (Radial::mapping_order());
49  const Real v (reference_point(Dim-1));
50 
51  // map in the base face
52  Point base_point;
53  switch (Dim)
54  {
55  case 1:
56  base_point = inf_elem->point(0);
57  break;
58  case 2:
59  base_point = FE<1,LAGRANGE>::map (base_elem.get(), reference_point);
60  break;
61  case 3:
62  base_point = FE<2,LAGRANGE>::map (base_elem.get(), reference_point);
63  break;
64  default:
65 #ifdef DEBUG
66  libmesh_error_msg("Unknown Dim = " << Dim);
67 #endif
68  break;
69  }
70 
71 
72  // map in the outer node face not necessary. Simply
73  // compute the outer_point = base_point + (base_point-origin)
74  const Point outer_point (base_point * 2. - inf_elem->origin());
75 
76  Point p;
77 
78  // there are only two mapping shapes in radial direction
79  p.add_scaled (base_point, InfFE<Dim,INFINITE_MAP,T_map>::eval (v, radial_mapping_order, 0));
80  p.add_scaled (outer_point, InfFE<Dim,INFINITE_MAP,T_map>::eval (v, radial_mapping_order, 1));
81 
82  return p;
83 }
libMesh::InfFE::Base::build_elem
static Elem * build_elem(const Elem *inf_elem)
Definition: inf_fe_base_radial.C:36
libMesh::FE::map
static Point map(const Elem *elem, const Point &reference_point)
Definition: fe_map.C:1985
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764
libMesh::InfFE::eval
static Real eval(Real v, Order o_radial, unsigned int i)
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::InfFE::Radial::mapping_order
static Order mapping_order()
Definition: inf_fe.h:131

◆ n_dofs()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
unsigned int libMesh::InfFE< Dim, T_radial, T_map >::n_dofs ( const FEType &  fet,
const ElemType  inf_elem_type 
)
static
Returns
The number of shape functions associated with this infinite element. Currently, we have o_radial+1 modes in radial direction, and
FE<Dim-1,T>::n_dofs(...)
in the base.

Definition at line 55 of file inf_fe_static.C.

References libMesh::FEInterface::n_dofs(), and libMesh::FEType::radial_order.

Referenced by libMesh::FEInterface::ifem_n_dofs(), and libMesh::InfFE< Dim, T_radial, T_map >::n_shape_functions().

57 {
58  const ElemType base_et (Base::get_elem_type(inf_elem_type));
59 
60  if (Dim > 1)
61  return FEInterface::n_dofs(Dim-1, fet, base_et) * Radial::n_dofs(fet.radial_order);
62  else
63  return Radial::n_dofs(fet.radial_order);
64 }
libMesh::FEInterface::n_dofs
static unsigned int n_dofs(const unsigned int dim, const FEType &fe_t, const ElemType t)
Definition: fe_interface.C:454
libMesh::InfFE::Base::get_elem_type
static ElemType get_elem_type(const ElemType type)
Definition: inf_fe_base_radial.C:51
libMesh::InfFE::Radial::n_dofs
static unsigned int n_dofs(const Order o_radial)
Definition: inf_fe.h:147

◆ n_dofs_at_node()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
unsigned int libMesh::InfFE< Dim, T_radial, T_map >::n_dofs_at_node ( const FEType &  fet,
const ElemType  inf_elem_type,
const unsigned int  n 
)
static
Returns
The number of dofs at infinite element node n (not dof!) for an element of type t and order o.

Definition at line 72 of file inf_fe_static.C.

References libMesh::FEInterface::n_dofs_at_node(), and libMesh::FEType::radial_order.

Referenced by libMesh::FEInterface::ifem_n_dofs_at_node().

75 {
76  const ElemType base_et (Base::get_elem_type(inf_elem_type));
77 
78  unsigned int n_base, n_radial;
79  compute_node_indices(inf_elem_type, n, n_base, n_radial);
80 
81  // libMesh::out << "elem_type=" << inf_elem_type
82  // << ", fet.radial_order=" << fet.radial_order
83  // << ", n=" << n
84  // << ", n_radial=" << n_radial
85  // << ", n_base=" << n_base
86  // << std::endl;
87 
88  if (Dim > 1)
89  return FEInterface::n_dofs_at_node(Dim-1, fet, base_et, n_base)
90  * Radial::n_dofs_at_node(fet.radial_order, n_radial);
91  else
92  return Radial::n_dofs_at_node(fet.radial_order, n_radial);
93 }
libMesh::InfFE::Radial::n_dofs_at_node
static unsigned int n_dofs_at_node(const Order o_radial, const unsigned int n_onion)
Definition: inf_fe_base_radial.C:124
libMesh::InfFE::Base::get_elem_type
static ElemType get_elem_type(const ElemType type)
Definition: inf_fe_base_radial.C:51
libMesh::InfFE::compute_node_indices
static void compute_node_indices(const ElemType inf_elem_type, const unsigned int outer_node_index, unsigned int &base_node, unsigned int &radial_node)
Definition: inf_fe_static.C:361
libMesh::FEInterface::n_dofs_at_node
static unsigned int n_dofs_at_node(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int n)
Definition: fe_interface.C:473

◆ n_dofs_per_elem()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
unsigned int libMesh::InfFE< Dim, T_radial, T_map >::n_dofs_per_elem ( const FEType &  fet,
const ElemType  inf_elem_type 
)
static
Returns
The number of dofs interior to the element, not associated with any interior nodes.

Definition at line 101 of file inf_fe_static.C.

References libMesh::FEInterface::n_dofs_per_elem(), and libMesh::FEType::radial_order.

Referenced by libMesh::FEInterface::ifem_n_dofs_per_elem().

103 {
104  const ElemType base_et (Base::get_elem_type(inf_elem_type));
105 
106  if (Dim > 1)
107  return FEInterface::n_dofs_per_elem(Dim-1, fet, base_et)
108  * Radial::n_dofs_per_elem(fet.radial_order);
109  else
110  return Radial::n_dofs_per_elem(fet.radial_order);
111 }
libMesh::FEInterface::n_dofs_per_elem
static unsigned int n_dofs_per_elem(const unsigned int dim, const FEType &fe_t, const ElemType t)
Definition: fe_interface.C:504
libMesh::InfFE::Base::get_elem_type
static ElemType get_elem_type(const ElemType type)
Definition: inf_fe_base_radial.C:51
libMesh::InfFE::Radial::n_dofs_per_elem
static unsigned int n_dofs_per_elem(const Order o_radial)
Definition: inf_fe.h:170

◆ n_objects()

static unsigned int libMesh::ReferenceCounter::n_objects ( )
inlinestaticinherited

Prints the number of outstanding (created, but not yet destroyed) objects.

Definition at line 83 of file reference_counter.h.

References libMesh::ReferenceCounter::_n_objects.

84  { return _n_objects; }
libMesh::ReferenceCounter::_n_objects
static Threads::atomic< unsigned int > _n_objects
Definition: reference_counter.h:130

◆ n_quadrature_points()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
virtual unsigned int libMesh::InfFE< Dim, T_radial, T_map >::n_quadrature_points ( ) const
inlineoverridevirtual
Returns
The total number of quadrature points. Call this to get an upper bound for the for loop in your simulation for matrix assembly of the current element.

Implements libMesh::FEAbstract.

Definition at line 468 of file inf_fe.h.

References libMesh::InfFE< Dim, T_radial, T_map >::_n_total_qp, and libMesh::InfFE< Dim, T_radial, T_map >::radial_qrule.

469  { libmesh_assert(radial_qrule); return _n_total_qp; }
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::InfFE::_n_total_qp
unsigned int _n_total_qp
Definition: inf_fe.h:740

◆ n_shape_functions() [1/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
static unsigned int libMesh::InfFE< Dim, T_radial, T_map >::n_shape_functions ( const FEType &  fet,
const ElemType  t 
)
inlinestatic
Returns
The number of shape functions associated with a finite element of type t and approximation order o.

Definition at line 301 of file inf_fe.h.

References libMesh::InfFE< Dim, T_radial, T_map >::n_dofs().

303  { return n_dofs(fet, t); }
libMesh::InfFE::n_dofs
static unsigned int n_dofs(const FEType &fet, const ElemType inf_elem_type)
Definition: inf_fe_static.C:55

◆ n_shape_functions() [2/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
virtual unsigned int libMesh::InfFE< Dim, T_radial, T_map >::n_shape_functions ( ) const
inlineoverridevirtual
Returns
The number of shape functions associated with this infinite element.

Implements libMesh::FEAbstract.

Definition at line 460 of file inf_fe.h.

References libMesh::InfFE< Dim, T_radial, T_map >::_n_total_approx_sf.

Referenced by libMesh::FEInterface::ifem_n_shape_functions().

461  { return _n_total_approx_sf; }
libMesh::InfFE::_n_total_approx_sf
unsigned int _n_total_approx_sf
Definition: inf_fe.h:734

◆ nodal_soln()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::nodal_soln ( const FEType &  fet,
const Elem *  elem,
const std::vector< Number > &  elem_soln,
std::vector< Number > &  nodal_soln 
)
static

Usually, this method would build the nodal soln from the element soln. But infinite elements require additional simulation-specific data to compute physically correct results. Use compute_data() to compute results. For compatibility an empty vector is returned.

Definition at line 119 of file inf_fe_static.C.

References libMesh::err.

Referenced by libMesh::FEInterface::ifem_nodal_soln().

123 {
124 #ifdef DEBUG
125  if (!_warned_for_nodal_soln)
126  {
127  libMesh::err << "WARNING: nodal_soln(...) does _not_ work for infinite elements." << std::endl
128  << " Will return an empty nodal solution. Use " << std::endl
129  << " InfFE<Dim,T_radial,T_map>::compute_data(..) instead!" << std::endl;
130  _warned_for_nodal_soln = true;
131  }
132 #endif
133 
134  /*
135  * In the base the infinite element couples to
136  * conventional finite elements. To not destroy
137  * the values there, clear \p nodal_soln. This
138  * indicates to the user of \p nodal_soln to
139  * not use this result.
140  */
141  nodal_soln.clear();
142  libmesh_assert (nodal_soln.empty());
143  return;
144 }
libMesh::err
OStreamProxy err(std::cerr)
Definition: libmesh_common.h:229
libMesh::InfFE::_warned_for_nodal_soln
static bool _warned_for_nodal_soln
Definition: inf_fe.h:807
libMesh::InfFE::nodal_soln
static void nodal_soln(const FEType &fet, const Elem *elem, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln)
Definition: inf_fe_static.C:119

◆ on_reference_element()

bool libMesh::FEAbstract::on_reference_element ( const Point &  p,
const ElemType  t,
const Real  eps = TOLERANCE 
)
staticinherited
Returns
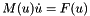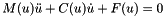true if the point p is located on the reference element for element type t, false otherwise. Since we are doing floating point comparisons here the parameter eps can be specified to indicate a tolerance. For example, $ x \le 1 $ becomes $ x \le 1 + \epsilon $.

Definition at line 581 of file fe_abstract.C.

References libMesh::EDGE2, libMesh::EDGE3, libMesh::EDGE4, libMesh::HEX20, libMesh::HEX27, libMesh::HEX8, libMesh::INFHEX16, libMesh::INFHEX18, libMesh::INFHEX8, libMesh::INFPRISM12, libMesh::INFPRISM6, libMesh::NODEELEM, libMesh::PRISM15, libMesh::PRISM18, libMesh::PRISM6, libMesh::PYRAMID13, libMesh::PYRAMID14, libMesh::PYRAMID5, libMesh::QUAD4, libMesh::QUAD8, libMesh::QUAD9, libMesh::QUADSHELL4, libMesh::QUADSHELL8, libMesh::Real, libMesh::TET10, libMesh::TET4, libMesh::TRI3, libMesh::TRI6, and libMesh::TRISHELL3.

Referenced by libMesh::FEInterface::ifem_on_reference_element(), libMesh::FE< Dim, LAGRANGE_VEC >::inverse_map(), and libMesh::FEInterface::on_reference_element().

582 {
583  libmesh_assert_greater_equal (eps, 0.);
584 
585  const Real xi = p(0);
586 #if LIBMESH_DIM > 1
587  const Real eta = p(1);
588 #else
589  const Real eta = 0.;
590 #endif
591 #if LIBMESH_DIM > 2
592  const Real zeta = p(2);
593 #else
594  const Real zeta = 0.;
595 #endif
596 
597  switch (t)
598  {
599  case NODEELEM:
600  {
601  return (!xi && !eta && !zeta);
602  }
603  case EDGE2:
604  case EDGE3:
605  case EDGE4:
606  {
607  // The reference 1D element is [-1,1].
608  if ((xi >= -1.-eps) &&
609  (xi <= 1.+eps))
610  return true;
611 
612  return false;
613  }
614 
615 
616  case TRI3:
617  case TRISHELL3:
618  case TRI6:
619  {
620  // The reference triangle is isosceles
621  // and is bound by xi=0, eta=0, and xi+eta=1.
622  if ((xi >= 0.-eps) &&
623  (eta >= 0.-eps) &&
624  ((xi + eta) <= 1.+eps))
625  return true;
626 
627  return false;
628  }
629 
630 
631  case QUAD4:
632  case QUADSHELL4:
633  case QUAD8:
634  case QUADSHELL8:
635  case QUAD9:
636  {
637  // The reference quadrilateral element is [-1,1]^2.
638  if ((xi >= -1.-eps) &&
639  (xi <= 1.+eps) &&
640  (eta >= -1.-eps) &&
641  (eta <= 1.+eps))
642  return true;
643 
644  return false;
645  }
646 
647 
648  case TET4:
649  case TET10:
650  {
651  // The reference tetrahedral is isosceles
652  // and is bound by xi=0, eta=0, zeta=0,
653  // and xi+eta+zeta=1.
654  if ((xi >= 0.-eps) &&
655  (eta >= 0.-eps) &&
656  (zeta >= 0.-eps) &&
657  ((xi + eta + zeta) <= 1.+eps))
658  return true;
659 
660  return false;
661  }
662 
663 
664  case HEX8:
665  case HEX20:
666  case HEX27:
667  {
668  /*
669  if ((xi >= -1.) &&
670  (xi <= 1.) &&
671  (eta >= -1.) &&
672  (eta <= 1.) &&
673  (zeta >= -1.) &&
674  (zeta <= 1.))
675  return true;
676  */
677 
678  // The reference hexahedral element is [-1,1]^3.
679  if ((xi >= -1.-eps) &&
680  (xi <= 1.+eps) &&
681  (eta >= -1.-eps) &&
682  (eta <= 1.+eps) &&
683  (zeta >= -1.-eps) &&
684  (zeta <= 1.+eps))
685  {
686  // libMesh::out << "Strange Point:\n";
687  // p.print();
688  return true;
689  }
690 
691  return false;
692  }
693 
694  case PRISM6:
695  case PRISM15:
696  case PRISM18:
697  {
698  // Figure this one out...
699  // inside the reference triangle with zeta in [-1,1]
700  if ((xi >= 0.-eps) &&
701  (eta >= 0.-eps) &&
702  (zeta >= -1.-eps) &&
703  (zeta <= 1.+eps) &&
704  ((xi + eta) <= 1.+eps))
705  return true;
706 
707  return false;
708  }
709 
710 
711  case PYRAMID5:
712  case PYRAMID13:
713  case PYRAMID14:
714  {
715  // Check that the point is on the same side of all the faces
716  // by testing whether:
717  //
718  // n_i.(x - x_i) <= 0
719  //
720  // for each i, where:
721  // n_i is the outward normal of face i,
722  // x_i is a point on face i.
723  if ((-eta - 1. + zeta <= 0.+eps) &&
724  ( xi - 1. + zeta <= 0.+eps) &&
725  ( eta - 1. + zeta <= 0.+eps) &&
726  ( -xi - 1. + zeta <= 0.+eps) &&
727  ( zeta >= 0.-eps))
728  return true;
729 
730  return false;
731  }
732 
733 #ifdef LIBMESH_ENABLE_INFINITE_ELEMENTS
734  case INFHEX8:
735  case INFHEX16:
736  case INFHEX18:
737  {
738  // The reference infhex8 is a [-1,1]^3.
739  if ((xi >= -1.-eps) &&
740  (xi <= 1.+eps) &&
741  (eta >= -1.-eps) &&
742  (eta <= 1.+eps) &&
743  (zeta >= -1.-eps) &&
744  (zeta <= 1.+eps))
745  {
746  return true;
747  }
748  return false;
749  }
750 
751  case INFPRISM6:
752  case INFPRISM12:
753  {
754  // inside the reference triangle with zeta in [-1,1]
755  if ((xi >= 0.-eps) &&
756  (eta >= 0.-eps) &&
757  (zeta >= -1.-eps) &&
758  (zeta <= 1.+eps) &&
759  ((xi + eta) <= 1.+eps))
760  {
761  return true;
762  }
763 
764  return false;
765  }
766 #endif
767 
768  default:
769  libmesh_error_msg("ERROR: Unknown element type " << t);
770  }
771 
772  // If we get here then the point is _not_ in the
773  // reference element. Better return false.
774 
775  return false;
776 }
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131

◆ print_d2phi()

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::print_d2phi ( std::ostream &  os) const
virtualinherited

Prints the value of each shape function's second derivatives at each quadrature point.

Implements libMesh::FEAbstract.

Definition at line 776 of file fe_base.C.

777 {
778  for (auto i : index_range(dphi))
779  for (auto j : index_range(dphi[i]))
780  os << " d2phi[" << i << "][" << j << "]=" << d2phi[i][j];
781 }
libMesh::FEGenericBase::d2phi
std::vector< std::vector< OutputTensor > > d2phi
Definition: fe_base.h:551
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503

◆ print_dphi()

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::print_dphi ( std::ostream &  os) const
virtualinherited

Prints the value of each shape function's derivative at each quadrature point.

Implements libMesh::FEAbstract.

Definition at line 718 of file fe_base.C.

719 {
720  for (auto i : index_range(dphi))
721  for (auto j : index_range(dphi[i]))
722  os << " dphi[" << i << "][" << j << "]=" << dphi[i][j];
723 }
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::FEGenericBase::dphi
std::vector< std::vector< OutputGradient > > dphi
Definition: fe_base.h:503

◆ print_info() [1/2]

void libMesh::ReferenceCounter::print_info ( std::ostream &  out = libMesh::out)
staticinherited

Prints the reference information, by default to libMesh::out.

Definition at line 87 of file reference_counter.C.

References libMesh::ReferenceCounter::_enable_print_counter, and libMesh::ReferenceCounter::get_info().

88 {
89  if (_enable_print_counter)
90  out_stream << ReferenceCounter::get_info();
91 }
libMesh::ReferenceCounter::get_info
static std::string get_info()
Definition: reference_counter.C:47

◆ print_info() [2/2]

void libMesh::FEAbstract::print_info ( std::ostream &  os) const
inherited

Prints all the relevant information about the current element.

Definition at line 793 of file fe_abstract.C.

References libMesh::FEAbstract::print_dphi(), libMesh::FEAbstract::print_JxW(), libMesh::FEAbstract::print_phi(), and libMesh::FEAbstract::print_xyz().

Referenced by libMesh::operator<<().

794 {
795  os << "phi[i][j]: Shape function i at quadrature pt. j" << std::endl;
796  this->print_phi(os);
797 
798  os << "dphi[i][j]: Shape function i's gradient at quadrature pt. j" << std::endl;
799  this->print_dphi(os);
800 
801  os << "XYZ locations of the quadrature pts." << std::endl;
802  this->print_xyz(os);
803 
804  os << "Values of JxW at the quadrature pts." << std::endl;
805  this->print_JxW(os);
806 }
libMesh::FEAbstract::print_phi
virtual void print_phi(std::ostream &os) const =0
libMesh::FEAbstract::print_dphi
virtual void print_dphi(std::ostream &os) const =0
libMesh::FEAbstract::print_xyz
void print_xyz(std::ostream &os) const
Definition: fe_abstract.C:787
libMesh::FEAbstract::print_JxW
void print_JxW(std::ostream &os) const
Definition: fe_abstract.C:780

◆ print_JxW()

void libMesh::FEAbstract::print_JxW ( std::ostream &  os) const
inherited

Prints the Jacobian times the weight for each quadrature point.

Definition at line 780 of file fe_abstract.C.

References libMesh::FEAbstract::_fe_map.

Referenced by libMesh::FEAbstract::print_info().

781 {
782  this->_fe_map->print_JxW(os);
783 }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ print_phi()

template<typename OutputType >
void libMesh::FEGenericBase< OutputType >::print_phi ( std::ostream &  os) const
virtualinherited

Prints the value of each shape function at each quadrature point.

Implements libMesh::FEAbstract.

Definition at line 707 of file fe_base.C.

708 {
709  for (auto i : index_range(phi))
710  for (auto j : index_range(phi[i]))
711  os << " phi[" << i << "][" << j << "]=" << phi[i][j] << std::endl;
712 }
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::FEGenericBase::phi
std::vector< std::vector< OutputShape > > phi
Definition: fe_base.h:498

◆ print_xyz()

void libMesh::FEAbstract::print_xyz ( std::ostream &  os) const
inherited

Prints the spatial location of each quadrature point (on the physical element).

Definition at line 787 of file fe_abstract.C.

References libMesh::FEAbstract::_fe_map.

Referenced by libMesh::FEAbstract::print_info().

788 {
789  this->_fe_map->print_xyz(os);
790 }
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525

◆ reinit() [1/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
void libMesh::InfFE< Dim, T_radial, T_map >::reinit ( const Elem *  elem,
const std::vector< Point > *const  pts = nullptr,
const std::vector< Real > *const  weights = nullptr 
)
overridevirtual

This is at the core of this class. Use this for each new element in the mesh. Reinitializes all the physical element-dependent data based on the current element elem.

Note
: pts need to be in reference space coordinates, not physical ones.

Implements libMesh::FEAbstract.

Definition at line 109 of file inf_fe.C.

References libMesh::FEGenericBase< OutputType >::build(), libMesh::EDGE2, libMesh::index_range(), libMesh::Real, and libMesh::Elem::type().

112 {
113  libmesh_assert(base_fe.get());
114  libmesh_assert(inf_elem);
115 
116  // I don't understand infinite elements well enough to risk
117  // calculating too little. :-( RHS
118  this->calculate_phi = this->calculate_dphi = this->calculate_dphiref = true;
119  this->get_xyz();
120  this->determine_calculations();
121  base_fe->calculate_phi = base_fe->calculate_dphi = base_fe->calculate_dphiref = true;
122  base_fe->get_xyz();
123  base_fe->determine_calculations();
124 
125  if (pts == nullptr)
126  {
127  libmesh_assert(base_fe->qrule);
128  libmesh_assert_equal_to (base_fe->qrule, base_qrule.get());
129  libmesh_assert(radial_qrule.get());
130 
131  bool init_shape_functions_required = false;
132 
133  // init the radial data fields only when the radial order changes
134  if (current_fe_type.radial_order != fe_type.radial_order)
135  {
136  current_fe_type.radial_order = fe_type.radial_order;
137 
138  // Watch out: this call to QBase->init() only works for
139  // current_fe_type = const! To allow variable Order,
140  // the init() of QBase has to be modified...
141  radial_qrule->init(EDGE2);
142 
143  // initialize the radial shape functions
144  this->init_radial_shape_functions(inf_elem);
145 
146  init_shape_functions_required=true;
147  }
148 
149 
150  bool update_base_elem_required=true;
151 
152  // update the type in accordance to the current cell
153  // and reinit if the cell type has changed or (as in
154  // the case of the hierarchics) the shape functions
155  // depend on the particular element and need a reinit
156  if ((Dim != 1) &&
157  ((this->get_type() != inf_elem->type()) ||
158  (base_fe->shapes_need_reinit())))
159  {
160  // store the new element type, update base_elem
161  // here. Through \p update_base_elem_required,
162  // remember whether it has to be updated (see below).
163  elem_type = inf_elem->type();
164  this->update_base_elem(inf_elem);
165  update_base_elem_required=false;
166 
167  // initialize the base quadrature rule for the new element
168  base_qrule->init(base_elem->type());
169 
170  // initialize the shape functions in the base
171  base_fe->init_base_shape_functions(base_fe->qrule->get_points(),
172  base_elem.get());
173 
174  // compute the shape functions and map functions of base_fe
175  // before using them later in combine_base_radial.
176  base_fe->_fe_map->compute_map (base_fe->dim, base_fe->qrule->get_weights(),
177  base_elem.get(), base_fe->calculate_d2phi);
178  base_fe->compute_shape_functions(base_elem.get(), base_fe->qrule->get_points());
179 
180  init_shape_functions_required=true;
181  }
182 
183 
184  // when either the radial or base part change,
185  // we have to init the whole fields
186  if (init_shape_functions_required)
187  this->init_shape_functions (radial_qrule->get_points(),
188  base_fe->qrule->get_points(),
189  inf_elem);
190 
191  // computing the distance only works when we have the current
192  // base_elem stored. This happens when fe_type is const,
193  // the inf_elem->type remains the same. Then we have to
194  // update the base elem _here_.
195  if (update_base_elem_required)
196  this->update_base_elem(inf_elem);
197 
198  // compute dist (depends on geometry, therefore has to be updated for
199  // each and every new element), throw radial and base part together
200  this->combine_base_radial (inf_elem);
201 
202  this->_fe_map->compute_map (this->dim, _total_qrule_weights, inf_elem, this->calculate_d2phi);
203 
204  // Compute the shape functions and the derivatives
205  // at all quadrature points.
206  this->compute_shape_functions (inf_elem,base_fe->qrule->get_points());
207  }
208 
209  else // if pts != nullptr
210  {
211  // update the elem_type
212  elem_type = inf_elem->type();
213 
214  // We'll assume that pts is a tensor product mesh of points.
215  // That will handle the pts.size()==1 case that we care about
216  // right now, and it will generalize a bit, and it won't break
217  // the assumptions elsewhere in InfFE.
218  std::vector<Point> radial_pts;
219  for (auto p : index_range(*pts))
220  {
221  Real radius = (*pts)[p](Dim-1);
222  //IMHO this is a dangerous check:
223  // 1) it is not guaranteed that two points have numerically equal radii
224  // 2) if there several radii but not sorted/regular, this breaks
225  if (radial_pts.size() && radial_pts[0](0) == radius)
226  break;
227  radial_pts.push_back(Point(radius));
228  }
229  const std::size_t radial_pts_size = radial_pts.size();
230  const std::size_t base_pts_size = pts->size() / radial_pts_size;
231  // If we're a tensor product we should have no remainder
232  libmesh_assert_equal_to
233  (base_pts_size * radial_pts_size, pts->size());
234 
235  if (pts->size() > 1)
236  {
237  // lets inform the user about our assumptions.
238  // If this warning appears very often, this should be taken as a reason
239  // for rewriting this.
240  libmesh_experimental();
241  libmesh_warning("We assume that the "<<pts->size()
242  <<" points are of tensor-product type with "
243  <<radial_pts_size<<" radial points and "
244  <<base_pts_size<< " angular points.");
245  }
246 
247 
248  std::vector<Point> base_pts;
249  base_pts.reserve(base_pts_size);
250  for (std::size_t p=0; p != pts->size(); p += radial_pts_size)
251  {
252  Point pt = (*pts)[p];
253  pt(Dim-1) = 0;
254  base_pts.push_back(pt);
255  }
256 
257  // init radial shapes
258  this->init_radial_shape_functions(inf_elem, &radial_pts);
259 
260  // update the base
261  this->update_base_elem(inf_elem);
262 
263  // the finite element on the ifem base
264  base_fe = FEBase::build(Dim-1, this->fe_type);
265 
266  base_fe->calculate_phi = base_fe->calculate_dphi = base_fe->calculate_dphiref = true;
267  base_fe->get_xyz();
268  base_fe->determine_calculations();
269 
270  // init base shapes
271  base_fe->init_base_shape_functions(base_pts,
272  base_elem.get());
273 
274  // compute the shape functions and map functions of base_fe
275  // before using them later in combine_base_radial.
276 
277  if (weights)
278  {
279  base_fe->_fe_map->compute_map (base_fe->dim, *weights,
280  base_elem.get(), base_fe->calculate_d2phi);
281  }
282  else
283  {
284  std::vector<Real> dummy_weights (pts->size(), 1.);
285  base_fe->_fe_map->compute_map (base_fe->dim, dummy_weights,
286  base_elem.get(), base_fe->calculate_d2phi);
287  }
288 
289  base_fe->compute_shape_functions(base_elem.get(), *pts);
290 
291  this->init_shape_functions (radial_pts, base_pts, inf_elem);
292 
293  // combine the base and radial shapes
294  this->combine_base_radial (inf_elem);
295 
296  // weights
297  if (weights != nullptr)
298  {
299  this->_fe_map->compute_map (this->dim, *weights, inf_elem, this->calculate_d2phi);
300  }
301  else
302  {
303  std::vector<Real> dummy_weights (pts->size(), 1.);
304  this->_fe_map->compute_map (this->dim, dummy_weights, inf_elem, this->calculate_d2phi);
305  }
306 
307  // finally compute the ifem shapes
308  this->compute_shape_functions (inf_elem,*pts);
309  }
310 
311 }
libMesh::FEAbstract::get_xyz
const std::vector< Point > & get_xyz() const
Definition: fe_abstract.h:238
libMesh::InfFE::combine_base_radial
void combine_base_radial(const Elem *inf_elem)
Definition: inf_fe.C:733
libMesh::FEAbstract::get_type
ElemType get_type() const
Definition: fe_abstract.h:418
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::FEType::radial_order
OrderWrapper radial_order
Definition: fe_type.h:237
libMesh::InfFE::init_shape_functions
void init_shape_functions(const std::vector< Point > &radial_qp, const std::vector< Point > &base_qp, const Elem *inf_elem)
Definition: inf_fe.C:404
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::InfFE::compute_shape_functions
virtual void compute_shape_functions(const Elem *, const std::vector< Point > &) override
Definition: inf_fe.C:878
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::FEGenericBase::build
static std::unique_ptr< FEGenericBase > build(const unsigned int dim, const FEType &type)
libMesh::InfFE::current_fe_type
FEType current_fe_type
Definition: inf_fe.h:782
libMesh::FEGenericBase::determine_calculations
void determine_calculations()
Definition: fe_base.C:728
libMesh::InfFE::init_radial_shape_functions
void init_radial_shape_functions(const Elem *inf_elem, const std::vector< Point > *radial_pts=nullptr)
Definition: inf_fe.C:320
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::InfFE::base_qrule
std::unique_ptr< QBase > base_qrule
Definition: inf_fe.h:752
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525
libMesh::InfFE::_total_qrule_weights
std::vector< Real > _total_qrule_weights
Definition: inf_fe.h:746
libMesh::InfFE::update_base_elem
void update_base_elem(const Elem *inf_elem)
Definition: inf_fe.C:98

◆ reinit() [2/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_base>
void libMesh::InfFE< Dim, T_radial, T_base >::reinit ( const Elem *  elem,
const unsigned int  side,
const Real  tolerance = TOLERANCE,
const std::vector< Point > *const  pts = nullptr,
const std::vector< Real > *const  weights = nullptr 
)
overridevirtual

Not implemented yet. Reinitializes all the physical element-dependent data based on the side of an infinite element.

Implements libMesh::FEAbstract.

Definition at line 36 of file inf_fe_boundary.C.

References libMesh::Elem::build_side_ptr(), libMesh::EDGE2, libMesh::Elem::p_level(), side, and libMesh::Elem::type().

41 {
42  if (weights != nullptr)
43  libmesh_not_implemented_msg("ERROR: User-specified weights for infinite elements are not implemented!");
44 
45  if (pts != nullptr)
46  libmesh_not_implemented_msg("ERROR: User-specified points for infinite elements are not implemented!");
47 
48  // We don't do this for 1D elements!
49  libmesh_assert_not_equal_to (Dim, 1);
50 
51  libmesh_assert(inf_elem);
52  libmesh_assert(qrule);
53 
54  // Don't do this for the base
55  libmesh_assert_not_equal_to (s, 0);
56 
57  // Build the side of interest
58  const std::unique_ptr<const Elem> side(inf_elem->build_side_ptr(s));
59 
60  // set the element type
61  elem_type = inf_elem->type();
62 
63  // eventually initialize radial quadrature rule
64  bool radial_qrule_initialized = false;
65 
66  if (current_fe_type.radial_order != fe_type.radial_order)
67  {
68  current_fe_type.radial_order = fe_type.radial_order;
69  radial_qrule->init(EDGE2, inf_elem->p_level());
70  radial_qrule_initialized = true;
71  }
72 
73  // Initialize the face shape functions
74  if (this->get_type() != inf_elem->type() ||
75  base_fe->shapes_need_reinit() ||
76  radial_qrule_initialized)
77  this->init_face_shape_functions (qrule->get_points(), side.get());
78 
79 
80  // compute the face map
81  this->_fe_map->compute_face_map(this->dim, _total_qrule_weights, side.get());
82 
83  // make a copy of the Jacobian for integration
84  const std::vector<Real> JxW_int(this->_fe_map->get_JxW());
85 
86  // Find where the integration points are located on the
87  // full element.
88  std::vector<Point> qp; this->inverse_map (inf_elem, this->_fe_map->get_xyz(),
89  qp, tolerance);
90 
91  // compute the shape function and derivative values
92  // at the points qp
93  this->reinit (inf_elem, &qp);
94 
95  // copy back old data
96  this->_fe_map->get_JxW() = JxW_int;
97 
98 }
libMesh::InfFE::init_face_shape_functions
void init_face_shape_functions(const std::vector< Point > &qp, const Elem *side)
Definition: inf_fe_boundary.C:122
libMesh::FEAbstract::get_type
ElemType get_type() const
Definition: fe_abstract.h:418
libMesh::InfFE::radial_qrule
std::unique_ptr< QBase > radial_qrule
Definition: inf_fe.h:758
libMesh::FEType::radial_order
OrderWrapper radial_order
Definition: fe_type.h:237
side
unsigned short int side
Definition: xdr_io.C:50
libMesh::FEAbstract::dim
const unsigned int dim
Definition: fe_abstract.h:531
libMesh::InfFE::base_fe
std::unique_ptr< FEBase > base_fe
Definition: inf_fe.h:772
libMesh::InfFE::current_fe_type
FEType current_fe_type
Definition: inf_fe.h:782
libMesh::InfFE::inverse_map
static Point inverse_map(const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true)
Definition: inf_fe_map.C:90
libMesh::QBase::get_points
const std::vector< Point > & get_points() const
Definition: quadrature.h:142
libMesh::InfFE::reinit
virtual void reinit(const Elem *elem, const std::vector< Point > *const pts=nullptr, const std::vector< Real > *const weights=nullptr) override
Definition: inf_fe.C:109
libMesh::FEAbstract::_fe_map
std::unique_ptr< FEMap > _fe_map
Definition: fe_abstract.h:525
libMesh::InfFE::_total_qrule_weights
std::vector< Real > _total_qrule_weights
Definition: inf_fe.h:746

◆ set_fe_order()

void libMesh::FEAbstract::set_fe_order ( int  new_order)
inlineinherited

Sets the base FE order of the finite element.

Definition at line 439 of file fe_abstract.h.

References libMesh::FEAbstract::fe_type, and libMesh::FEType::order.

439 { fe_type.order = new_order; }
libMesh::FEType::order
OrderWrapper order
Definition: fe_type.h:198

◆ shape() [1/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
Real libMesh::InfFE< Dim, T_radial, T_map >::shape ( const FEType &  fet,
const ElemType  t,
const unsigned int  i,
const Point &  p 
)
static
Returns
The value of the 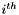$ i^{th} $ shape function at point p. This method lets you specify the relevant data directly, and is therefore allowed to be static.
Note
This class member is not as efficient as its counterpart in FE<Dim,T>, and is not employed in the reinit() cycle.
This method does not return physically correct shapes, instead use compute_data(). The shape() methods should only be used for mapping.

Definition at line 154 of file inf_fe_static.C.

References libMesh::InfFE< Dim, T_radial, T_map >::Radial::decay(), libMesh::err, libMesh::InfFE< Dim, T_radial, T_map >::eval(), libMesh::INFINITE_MAP, libMesh::FEType::radial_order, libMesh::Real, and libMesh::FEInterface::shape().

Referenced by libMesh::FEInterface::ifem_shape().

158 {
159  libmesh_assert_not_equal_to (Dim, 0);
160 
161 #ifdef DEBUG
162  // this makes only sense when used for mapping
163  if ((T_radial != INFINITE_MAP) && !_warned_for_shape)
164  {
165  libMesh::err << "WARNING: InfFE<Dim,T_radial,T_map>::shape(...) does _not_" << std::endl
166  << " return the correct trial function! Use " << std::endl
167  << " InfFE<Dim,T_radial,T_map>::compute_data(..) instead!"
168  << std::endl;
169  _warned_for_shape = true;
170  }
171 #endif
172 
173  const ElemType base_et (Base::get_elem_type(inf_elem_type));
174  const Order o_radial (fet.radial_order);
175  const Real v (p(Dim-1));
176 
177  unsigned int i_base, i_radial;
178  compute_shape_indices(fet, inf_elem_type, i, i_base, i_radial);
179 
180  //TODO:[SP/DD] exp(ikr) is still missing here!
181  // but is it intended? It would be probably somehow nice, but than it would be Number, not Real !
182  // --> thus it would destroy the interface...
183  if (Dim > 1)
184  return FEInterface::shape(Dim-1, fet, base_et, i_base, p)
185  * InfFE<Dim,T_radial,T_map>::eval(v, o_radial, i_radial)
186  * InfFE<Dim,T_radial,T_map>::Radial::decay(v);
187  else
188  return InfFE<Dim,T_radial,T_map>::eval(v, o_radial, i_radial)
189  * InfFE<Dim,T_radial,T_map>::Radial::decay(v);
190 }
libMesh::InfFE::_warned_for_shape
static bool _warned_for_shape
Definition: inf_fe.h:808
libMesh::InfFE::Base::get_elem_type
static ElemType get_elem_type(const ElemType type)
Definition: inf_fe_base_radial.C:51
libMesh::InfFE::Radial::decay
static Real decay(const Real v)
Definition: inf_fe.h:827
libMesh::FEInterface::shape
static Real shape(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int i, const Point &p)
Definition: fe_interface.C:657
libMesh::InfFE::eval
static Real eval(Real v, Order o_radial, unsigned int i)
libMesh::err
OStreamProxy err(std::cerr)
Definition: libmesh_common.h:229
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::InfFE::compute_shape_indices
static void compute_shape_indices(const FEType &fet, const ElemType inf_elem_type, const unsigned int i, unsigned int &base_shape, unsigned int &radial_shape)
Definition: inf_fe_static.C:677

◆ shape() [2/2]

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
Real libMesh::InfFE< Dim, T_radial, T_map >::shape ( const FEType &  fet,
const Elem *  elem,
const unsigned int  i,
const Point &  p 
)
static
Returns
The value of the 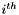$ i^{th} $ shape function at point p. This method lets you specify the relevant data directly, and is therefore allowed to be static.
Note
This class member is not as efficient as its counterpart in FE<Dim,T>, and is not employed in the reinit() cycle.
This method does not return physically correct shapes, instead use compute_data(). The shape() methods should only be used for mapping.

Definition at line 198 of file inf_fe_static.C.

References libMesh::Elem::build_side_ptr(), libMesh::InfFE< Dim, T_radial, T_map >::Radial::decay(), libMesh::err, libMesh::InfFE< Dim, T_radial, T_map >::eval(), libMesh::INFINITE_MAP, libMesh::FEType::radial_order, libMesh::Real, libMesh::FEInterface::shape(), and libMesh::Elem::type().

202 {
203  libmesh_assert(inf_elem);
204  libmesh_assert_not_equal_to (Dim, 0);
205 
206 #ifdef DEBUG
207  // this makes only sense when used for mapping
208  if ((T_radial != INFINITE_MAP) && !_warned_for_shape)
209  {
210  libMesh::err << "WARNING: InfFE<Dim,T_radial,T_map>::shape(...) does _not_" << std::endl
211  << " return the correct trial function! Use " << std::endl
212  << " InfFE<Dim,T_radial,T_map>::compute_data(..) instead!"
213  << std::endl;
214  _warned_for_shape = true;
215  }
216 #endif
217 
218  const Order o_radial (fet.radial_order);
219  const Real v (p(Dim-1));
220  std::unique_ptr<const Elem> base_el (inf_elem->build_side_ptr(0));
221 
222  unsigned int i_base, i_radial;
223  compute_shape_indices(fet, inf_elem->type(), i, i_base, i_radial);
224 
225  if (Dim > 1)
226  return FEInterface::shape(Dim-1, fet, base_el.get(), i_base, p)
227  * InfFE<Dim,T_radial,T_map>::eval(v, o_radial, i_radial)
228  * InfFE<Dim,T_radial,T_map>::Radial::decay(v);
229  else
230  return InfFE<Dim,T_radial,T_map>::eval(v, o_radial, i_radial)
231  * InfFE<Dim,T_radial,T_map>::Radial::decay(v);
232 }
libMesh::InfFE::_warned_for_shape
static bool _warned_for_shape
Definition: inf_fe.h:808
libMesh::InfFE::Radial::decay
static Real decay(const Real v)
Definition: inf_fe.h:827
libMesh::FEInterface::shape
static Real shape(const unsigned int dim, const FEType &fe_t, const ElemType t, const unsigned int i, const Point &p)
Definition: fe_interface.C:657
libMesh::InfFE::eval
static Real eval(Real v, Order o_radial, unsigned int i)
libMesh::err
OStreamProxy err(std::cerr)
Definition: libmesh_common.h:229
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131
libMesh::InfFE::compute_shape_indices
static void compute_shape_indices(const FEType &fet, const ElemType inf_elem_type, const unsigned int i, unsigned int &base_shape, unsigned int &radial_shape)
Definition: inf_fe_static.C:677

◆ shapes_need_reinit()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
bool libMesh::InfFE< Dim, T_radial, T_map >::shapes_need_reinit ( ) const
overrideprivatevirtual
Returns
false, currently not required.

Implements libMesh::FEAbstract.

Definition at line 980 of file inf_fe.C.

981 {
982  return false;
983 }

◆ side_map()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
virtual void libMesh::InfFE< Dim, T_radial, T_map >::side_map ( const Elem *  ,
const Elem *  ,
const unsigned int  ,
const std::vector< Point > &  ,
std::vector< Point > &   
)
inlineoverridevirtual

Computes the reference space quadrature points on the side of an element based on the side quadrature points.

Implements libMesh::FEAbstract.

Definition at line 434 of file inf_fe.h.

439  {
440  libmesh_not_implemented();
441  }

◆ update_base_elem()

template<unsigned int Dim, FEFamily T_radial, InfMapType T_base>
void libMesh::InfFE< Dim, T_radial, T_base >::update_base_elem ( const Elem *  inf_elem)
protected

Updates the protected member base_elem to the appropriate base element for the given inf_elem.

Definition at line 98 of file inf_fe.C.

99 {
100  base_elem.reset(Base::build_elem(inf_elem));
101 }
libMesh::InfFE::Base::build_elem
static Elem * build_elem(const Elem *inf_elem)
Definition: inf_fe_base_radial.C:36
libMesh::InfFE::base_elem
std::unique_ptr< Elem > base_elem
Definition: inf_fe.h:764

Friends And Related Function Documentation

◆ InfFE

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
template<unsigned int friend_Dim, FEFamily friend_T_radial, InfMapType friend_T_map>
friend class InfFE
friend

Make all InfFE<Dim,T_radial,T_map> classes friends of each other, so that the protected eval() may be accessed.

Definition at line 818 of file inf_fe.h.

Member Data Documentation

◆ _base_node_index

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<unsigned int> libMesh::InfFE< Dim, T_radial, T_map >::_base_node_index
protected

The internal structure of the InfFE – tensor product of base element times radial nodes – has to be determined from the node numbering of the current element. This vector maps the infinite Elem node number to the associated node in the base element.

Definition at line 703 of file inf_fe.h.

◆ _base_shape_index

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<unsigned int> libMesh::InfFE< Dim, T_radial, T_map >::_base_shape_index
protected

The internal structure of the InfFE – tensor product of base element shapes times radial shapes – has to be determined from the dof numbering scheme of the current infinite element. This vector maps the infinite Elem dof index to the associated dof in the base FE.

Definition at line 723 of file inf_fe.h.

◆ _compute_node_indices_fast_current_elem_type

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
ElemType libMesh::InfFE< Dim, T_radial, T_map >::_compute_node_indices_fast_current_elem_type = INVALID_ELEM
staticprivate

When compute_node_indices_fast() is used, this static variable remembers the element type for which the static variables in compute_node_indices_fast() are currently set. Using a class member for the element type helps initializing it to a default value.

Definition at line 799 of file inf_fe.h.

◆ _counts

ReferenceCounter::Counts libMesh::ReferenceCounter::_counts
staticprotectedinherited

Actually holds the data.

Definition at line 122 of file reference_counter.h.

Referenced by libMesh::ReferenceCounter::get_info(), libMesh::ReferenceCounter::increment_constructor_count(), and libMesh::ReferenceCounter::increment_destructor_count().

◆ _enable_print_counter

bool libMesh::ReferenceCounter::_enable_print_counter = true
staticprotectedinherited

Flag to control whether reference count information is printed when print_info is called.

Definition at line 141 of file reference_counter.h.

Referenced by libMesh::ReferenceCounter::disable_print_counter_info(), libMesh::ReferenceCounter::enable_print_counter_info(), and libMesh::ReferenceCounter::print_info().

◆ _fe_map

std::unique_ptr<FEMap> libMesh::FEAbstract::_fe_map
protectedinherited

Definition at line 525 of file fe_abstract.h.

Referenced by libMesh::FEAbstract::get_curvatures(), libMesh::FEAbstract::get_d2xyzdeta2(), libMesh::FEAbstract::get_d2xyzdetadzeta(), libMesh::FEAbstract::get_d2xyzdxi2(), libMesh::FEAbstract::get_d2xyzdxideta(), libMesh::FEAbstract::get_d2xyzdxidzeta(), libMesh::FEAbstract::get_d2xyzdzeta2(), libMesh::FEAbstract::get_detadx(), libMesh::FEAbstract::get_detady(), libMesh::FEAbstract::get_detadz(), libMesh::FEAbstract::get_dxidx(), libMesh::FEAbstract::get_dxidy(), libMesh::FEAbstract::get_dxidz(), libMesh::FEAbstract::get_dxyzdeta(), libMesh::FEAbstract::get_dxyzdxi(), libMesh::FEAbstract::get_dxyzdzeta(), libMesh::FEAbstract::get_dzetadx(), libMesh::FEAbstract::get_dzetady(), libMesh::FEAbstract::get_dzetadz(), libMesh::FEAbstract::get_fe_map(), libMesh::FEAbstract::get_JxW(), libMesh::FEAbstract::get_normals(), libMesh::FEAbstract::get_tangents(), libMesh::FEAbstract::get_xyz(), libMesh::FESubdivision::init_shape_functions(), libMesh::FEAbstract::print_JxW(), and libMesh::FEAbstract::print_xyz().

◆ _fe_trans

template<typename OutputType>
std::unique_ptr<FETransformationBase<OutputType> > libMesh::FEGenericBase< OutputType >::_fe_trans
protectedinherited

Object that handles computing shape function values, gradients, etc in the physical domain.

Definition at line 493 of file fe_base.h.

◆ _mutex

Threads::spin_mutex libMesh::ReferenceCounter::_mutex
staticprotectedinherited

Mutual exclusion object to enable thread-safe reference counting.

Definition at line 135 of file reference_counter.h.

◆ _n_objects

Threads::atomic< unsigned int > libMesh::ReferenceCounter::_n_objects
staticprotectedinherited

The number of objects. Print the reference count information when the number returns to 0.

Definition at line 130 of file reference_counter.h.

Referenced by libMesh::ReferenceCounter::n_objects(), libMesh::ReferenceCounter::ReferenceCounter(), and libMesh::ReferenceCounter::~ReferenceCounter().

◆ _n_total_approx_sf

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
unsigned int libMesh::InfFE< Dim, T_radial, T_map >::_n_total_approx_sf
protected

The number of total approximation shape functions for the current configuration

Definition at line 734 of file inf_fe.h.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::n_shape_functions().

◆ _n_total_qp

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
unsigned int libMesh::InfFE< Dim, T_radial, T_map >::_n_total_qp
protected

The total number of quadrature points for the current configuration

Definition at line 740 of file inf_fe.h.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::n_quadrature_points().

◆ _p_level

unsigned int libMesh::FEAbstract::_p_level
protectedinherited

The p refinement level the current data structures are set up for.

Definition at line 587 of file fe_abstract.h.

Referenced by libMesh::FEAbstract::get_order(), and libMesh::FEAbstract::get_p_level().

◆ _radial_node_index

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<unsigned int> libMesh::InfFE< Dim, T_radial, T_map >::_radial_node_index
protected

The internal structure of the InfFE – tensor product of base element times radial nodes – has to be determined from the node numbering of the current infinite element. This vector maps the infinite Elem node number to the radial node (either 0 or 1).

Definition at line 693 of file inf_fe.h.

◆ _radial_shape_index

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<unsigned int> libMesh::InfFE< Dim, T_radial, T_map >::_radial_shape_index
protected

The internal structure of the InfFE – tensor product of base element shapes times radial shapes – has to be determined from the dof numbering scheme of the current infinite element. This vector maps the infinite Elem dof index to the radial InfFE shape index (0..radial_order+1 ).

Definition at line 713 of file inf_fe.h.

◆ _total_qrule_weights

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::_total_qrule_weights
protected

this vector contains the combined integration weights, so that FEAbstract::compute_map() can still be used

Definition at line 746 of file inf_fe.h.

◆ _warned_for_nodal_soln

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
bool libMesh::InfFE< Dim, T_radial, T_map >::_warned_for_nodal_soln = false
staticprivate

static members that are used to issue warning messages only once.

Definition at line 807 of file inf_fe.h.

◆ _warned_for_shape

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
bool libMesh::InfFE< Dim, T_radial, T_map >::_warned_for_shape = false
staticprivate

Definition at line 808 of file inf_fe.h.

◆ base_elem

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::unique_ptr<Elem> libMesh::InfFE< Dim, T_radial, T_map >::base_elem
protected

The base element associated with the current infinite element

Definition at line 764 of file inf_fe.h.

◆ base_fe

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::unique_ptr<FEBase> libMesh::InfFE< Dim, T_radial, T_map >::base_fe
protected

Have a FE<Dim-1,T_base> handy for base approximation. Since this one is created using the FEBase::build() method, the InfFE class is not required to be templated w.r.t. to the base approximation shape.

Definition at line 772 of file inf_fe.h.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::InfFE().

◆ base_qrule

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::unique_ptr<QBase> libMesh::InfFE< Dim, T_radial, T_map >::base_qrule
protected

The quadrature rule for the base element associated with the current infinite element

Definition at line 752 of file inf_fe.h.

◆ calculate_curl_phi

bool libMesh::FEAbstract::calculate_curl_phi
mutableprotectedinherited

Should we calculate shape function curls?

Definition at line 557 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi().

◆ calculate_d2phi

bool libMesh::FEAbstract::calculate_d2phi
mutableprotectedinherited

Should we calculate shape function hessians?

Definition at line 552 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2(), and libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2().

◆ calculate_div_phi

bool libMesh::FEAbstract::calculate_div_phi
mutableprotectedinherited

Should we calculate shape function divergences?

Definition at line 562 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi().

◆ calculate_dphi

bool libMesh::FEAbstract::calculate_dphi
mutableprotectedinherited

Should we calculate shape function gradients?

Definition at line 547 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy(), and libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz().

◆ calculate_dphiref

bool libMesh::FEAbstract::calculate_dphiref
mutableprotectedinherited

Should we calculate reference shape function gradients?

Definition at line 567 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidxi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz(), and libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidzeta().

◆ calculate_phi

bool libMesh::FEAbstract::calculate_phi
mutableprotectedinherited

Should we calculate shape functions?

Definition at line 542 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_phi().

◆ calculations_started

bool libMesh::FEAbstract::calculations_started
mutableprotectedinherited

Have calculations with this object already been started? Then all get_* functions should already have been called.

Definition at line 537 of file fe_abstract.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidxi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_phi(), and libMesh::FESubdivision::init_shape_functions().

◆ curl_phi

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::curl_phi
protectedinherited

Shape function curl values. Only defined for vector types.

Definition at line 508 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi().

◆ current_fe_type

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
FEType libMesh::InfFE< Dim, T_radial, T_map >::current_fe_type
protected

This FEType stores the characteristics for which the data structures phi, phi_map etc are currently initialized. This avoids re-initializing the radial part.

Note
Currently only order may change, both the FE families and base_order must remain constant.

Definition at line 782 of file inf_fe.h.

◆ d2phi

template<typename OutputType>
std::vector<std::vector<OutputTensor> > libMesh::FEGenericBase< OutputType >::d2phi
protectedinherited

Shape function second derivative values.

Definition at line 551 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi().

◆ d2phideta2

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phideta2
protectedinherited

Shape function second derivatives in the eta direction.

Definition at line 571 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2().

◆ d2phidetadzeta

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidetadzeta
protectedinherited

Shape function second derivatives in the eta-zeta direction.

Definition at line 576 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta().

◆ d2phidx2

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidx2
protectedinherited

Shape function second derivatives in the x direction.

Definition at line 586 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2().

◆ d2phidxdy

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidxdy
protectedinherited

Shape function second derivatives in the x-y direction.

Definition at line 591 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy().

◆ d2phidxdz

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidxdz
protectedinherited

Shape function second derivatives in the x-z direction.

Definition at line 596 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz().

◆ d2phidxi2

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidxi2
protectedinherited

Shape function second derivatives in the xi direction.

Definition at line 556 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2().

◆ d2phidxideta

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidxideta
protectedinherited

Shape function second derivatives in the xi-eta direction.

Definition at line 561 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta().

◆ d2phidxidzeta

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidxidzeta
protectedinherited

Shape function second derivatives in the xi-zeta direction.

Definition at line 566 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta().

◆ d2phidy2

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidy2
protectedinherited

Shape function second derivatives in the y direction.

Definition at line 601 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2().

◆ d2phidydz

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidydz
protectedinherited

Shape function second derivatives in the y-z direction.

Definition at line 606 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz().

◆ d2phidz2

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidz2
protectedinherited

Shape function second derivatives in the z direction.

Definition at line 611 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2().

◆ d2phidzeta2

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::d2phidzeta2
protectedinherited

Shape function second derivatives in the zeta direction.

Definition at line 581 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2().

◆ dim

const unsigned int libMesh::FEAbstract::dim
protectedinherited

The dimensionality of the object

Definition at line 531 of file fe_abstract.h.

Referenced by libMesh::FEAbstract::build(), and libMesh::FEAbstract::get_dim().

◆ dist

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::dist
protected

the radial distance of the base nodes from the origin

Definition at line 612 of file inf_fe.h.

◆ div_phi

template<typename OutputType>
std::vector<std::vector<OutputDivergence> > libMesh::FEGenericBase< OutputType >::div_phi
protectedinherited

Shape function divergence values. Only defined for vector types.

Definition at line 513 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi().

◆ dmodedv

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<std::vector<Real> > libMesh::InfFE< Dim, T_radial, T_map >::dmodedv
protected

the first local derivative of the radial approximation shapes. Needed when setting up the overall shape functions.

Definition at line 646 of file inf_fe.h.

◆ dphase

template<typename OutputType>
std::vector<OutputGradient> libMesh::FEGenericBase< OutputType >::dphase
protectedinherited

Used for certain infinite element families: the first derivatives of the phase term in global coordinates, over all quadrature points.

Definition at line 629 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphase().

◆ dphasedeta

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::dphasedeta
protected

the second local derivative (for 3D, the second in the base) of the phase term in local coordinates. Needed in the overall weak form of infinite element formulations.

Definition at line 671 of file inf_fe.h.

◆ dphasedxi

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::dphasedxi
protected

the first local derivative (for 3D, the first in the base) of the phase term in local coordinates. Needed in the overall weak form of infinite element formulations.

Definition at line 664 of file inf_fe.h.

◆ dphasedzeta

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::dphasedzeta
protected

the third local derivative (for 3D, the derivative in radial direction) of the phase term in local coordinates. Needed in the overall weak form of infinite element formulations.

Definition at line 678 of file inf_fe.h.

◆ dphi

template<typename OutputType>
std::vector<std::vector<OutputGradient> > libMesh::FEGenericBase< OutputType >::dphi
protectedinherited

Shape function derivative values.

Definition at line 503 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi().

◆ dphideta

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::dphideta
protectedinherited

Shape function derivatives in the eta direction.

Definition at line 523 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphideta().

◆ dphidx

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::dphidx
protectedinherited

Shape function derivatives in the x direction.

Definition at line 533 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx().

◆ dphidxi

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::dphidxi
protectedinherited

Shape function derivatives in the xi direction.

Definition at line 518 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidxi().

◆ dphidy

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::dphidy
protectedinherited

Shape function derivatives in the y direction.

Definition at line 538 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy().

◆ dphidz

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::dphidz
protectedinherited

Shape function derivatives in the z direction.

Definition at line 543 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz().

◆ dphidzeta

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::dphidzeta
protectedinherited

Shape function derivatives in the zeta direction.

Definition at line 528 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidzeta().

◆ dradialdv_map

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<std::vector<Real> > libMesh::InfFE< Dim, T_radial, T_map >::dradialdv_map
protected

the first local derivative of the radial mapping shapes

Definition at line 657 of file inf_fe.h.

◆ dsomdv

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::dsomdv
protected

the first local derivative of the radial decay $ 1/r $ in local coordinates. Needed when setting up the overall shape functions.

Definition at line 634 of file inf_fe.h.

◆ dweight

template<typename OutputType>
std::vector<RealGradient> libMesh::FEGenericBase< OutputType >::dweight
protectedinherited

Used for certain infinite element families: the global derivative of the additional radial weight $ 1/{r^2} $, over all quadrature points.

Definition at line 636 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_Sobolev_dweight().

◆ dweightdv

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::dweightdv
protected

the additional radial weight $ 1/{r^2} $ in local coordinates, over all quadrature points. The weight does not vary in base direction. However, for uniform access to the data fields from the outside, this data field is expanded to all quadrature points.

Definition at line 620 of file inf_fe.h.

◆ elem_type

ElemType libMesh::FEAbstract::elem_type
protectedinherited

The element type the current data structures are set up for.

Definition at line 581 of file fe_abstract.h.

Referenced by libMesh::FESubdivision::attach_quadrature_rule(), and libMesh::FEAbstract::get_type().

◆ fe_type

FEType libMesh::FEAbstract::fe_type
protectedinherited

The finite element type for this object.

Note
This should be constant for the object.

Definition at line 575 of file fe_abstract.h.

Referenced by libMesh::FEAbstract::compute_node_constraints(), libMesh::FEAbstract::compute_periodic_node_constraints(), libMesh::FEAbstract::get_family(), libMesh::FEAbstract::get_fe_type(), libMesh::FEAbstract::get_order(), libMesh::InfFE< Dim, T_radial, T_map >::InfFE(), libMesh::FESubdivision::init_shape_functions(), and libMesh::FEAbstract::set_fe_order().

◆ mode

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<std::vector<Real> > libMesh::InfFE< Dim, T_radial, T_map >::mode
protected

the radial approximation shapes in local coordinates Needed when setting up the overall shape functions.

Definition at line 640 of file inf_fe.h.

◆ phi

template<typename OutputType>
std::vector<std::vector<OutputShape> > libMesh::FEGenericBase< OutputType >::phi
protectedinherited

Shape function values.

Definition at line 498 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_phi().

◆ qrule

QBase* libMesh::FEAbstract::qrule
protectedinherited

A pointer to the quadrature rule employed

Definition at line 592 of file fe_abstract.h.

Referenced by libMesh::FESubdivision::attach_quadrature_rule().

◆ radial_map

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<std::vector<Real> > libMesh::InfFE< Dim, T_radial, T_map >::radial_map
protected

the radial mapping shapes in local coordinates

Definition at line 651 of file inf_fe.h.

◆ radial_qrule

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::unique_ptr<QBase> libMesh::InfFE< Dim, T_radial, T_map >::radial_qrule
protected

The quadrature rule for the base element associated with the current infinite element

Definition at line 758 of file inf_fe.h.

Referenced by libMesh::InfFE< Dim, T_radial, T_map >::n_quadrature_points().

◆ shapes_on_quadrature

bool libMesh::FEAbstract::shapes_on_quadrature
protectedinherited

A flag indicating if current data structures correspond to quadrature rule points

Definition at line 598 of file fe_abstract.h.

◆ som

template<unsigned int Dim, FEFamily T_radial, InfMapType T_map>
std::vector<Real> libMesh::InfFE< Dim, T_radial, T_map >::som
protected

the radial decay $ 1/r $ in local coordinates. Needed when setting up the overall shape functions.

Note
It is this decay which ensures that the Sommerfeld radiation condition is satisfied in advance.

Definition at line 629 of file inf_fe.h.

◆ weight

template<typename OutputType>
std::vector<Real> libMesh::FEGenericBase< OutputType >::weight
protectedinherited

Used for certain infinite element families: the additional radial weight 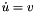$ 1/{r^2} $ in local coordinates, over all quadrature points.

Definition at line 643 of file fe_base.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_Sobolev_weight().

The documentation for this class was generated from the following files:
generated by doxygen