A matrix object used for finite element assembly and numerics. More...

#include <dense_matrix.h>

Inheritance diagram for libMesh::DenseMatrix< T >:

Public Member Functions
	DenseMatrix (const unsigned int new_m=0, const unsigned int new_n=0)

	DenseMatrix (DenseMatrix &&)=default

	DenseMatrix (const DenseMatrix &)=default

DenseMatrix &	operator= (const DenseMatrix &)=default

DenseMatrix &	operator= (DenseMatrix &&)=default

virtual	~DenseMatrix ()=default

virtual void	zero () override

T	operator() (const unsigned int i, const unsigned int j) const

T &	operator() (const unsigned int i, const unsigned int j)

virtual T	el (const unsigned int i, const unsigned int j) const override

virtual T &	el (const unsigned int i, const unsigned int j) override

virtual void	left_multiply (const DenseMatrixBase< T > &M2) override

template<typename T2 >
void	left_multiply (const DenseMatrixBase< T2 > &M2)

virtual void	right_multiply (const DenseMatrixBase< T > &M2) override

template<typename T2 >
void	right_multiply (const DenseMatrixBase< T2 > &M2)

void	vector_mult (DenseVector< T > &dest, const DenseVector< T > &arg) const

template<typename T2 >
void	vector_mult (DenseVector< typename CompareTypes< T, T2 >::supertype > &dest, const DenseVector< T2 > &arg) const

void	vector_mult_transpose (DenseVector< T > &dest, const DenseVector< T > &arg) const

template<typename T2 >
void	vector_mult_transpose (DenseVector< typename CompareTypes< T, T2 >::supertype > &dest, const DenseVector< T2 > &arg) const

void	vector_mult_add (DenseVector< T > &dest, const T factor, const DenseVector< T > &arg) const

template<typename T2 , typename T3 >
void	vector_mult_add (DenseVector< typename CompareTypes< T, typename CompareTypes< T2, T3 >::supertype >::supertype > &dest, const T2 factor, const DenseVector< T3 > &arg) const

void	get_principal_submatrix (unsigned int sub_m, unsigned int sub_n, DenseMatrix< T > &dest) const

void	get_principal_submatrix (unsigned int sub_m, DenseMatrix< T > &dest) const

void	outer_product (const DenseVector< T > &a, const DenseVector< T > &b)

template<typename T2 >
DenseMatrix< T > &	operator= (const DenseMatrix< T2 > &other_matrix)

void	swap (DenseMatrix< T > &other_matrix)

void	resize (const unsigned int new_m, const unsigned int new_n)

void	scale (const T factor)

void	scale_column (const unsigned int col, const T factor)

DenseMatrix< T > &	operator*= (const T factor)

template<typename T2 , typename T3 >
boostcopy::enable_if_c< ScalarTraits< T2 >::value, void >::type	add (const T2 factor, const DenseMatrix< T3 > &mat)

bool	operator== (const DenseMatrix< T > &mat) const

bool	operator!= (const DenseMatrix< T > &mat) const

DenseMatrix< T > &	operator+= (const DenseMatrix< T > &mat)

DenseMatrix< T > &	operator-= (const DenseMatrix< T > &mat)

Real	min () const

Real	max () const

Real	l1_norm () const

Real	linfty_norm () const

void	left_multiply_transpose (const DenseMatrix< T > &A)

template<typename T2 >
void	left_multiply_transpose (const DenseMatrix< T2 > &A)

void	right_multiply_transpose (const DenseMatrix< T > &A)

template<typename T2 >
void	right_multiply_transpose (const DenseMatrix< T2 > &A)

T	transpose (const unsigned int i, const unsigned int j) const

void	get_transpose (DenseMatrix< T > &dest) const

std::vector< T > &	get_values ()

const std::vector< T > &	get_values () const

void	condense (const unsigned int i, const unsigned int j, const T val, DenseVector< T > &rhs)

void	lu_solve (const DenseVector< T > &b, DenseVector< T > &x)

template<typename T2 >
void	cholesky_solve (const DenseVector< T2 > &b, DenseVector< T2 > &x)

void	svd (DenseVector< Real > &sigma)

void	svd (DenseVector< Real > &sigma, DenseMatrix< Number > &U, DenseMatrix< Number > &VT)

void	svd_solve (const DenseVector< T > &rhs, DenseVector< T > &x, Real rcond=std::numeric_limits< Real >::epsilon()) const

void	evd (DenseVector< T > &lambda_real, DenseVector< T > &lambda_imag)

void	evd_left (DenseVector< T > &lambda_real, DenseVector< T > &lambda_imag, DenseMatrix< T > &VL)

void	evd_right (DenseVector< T > &lambda_real, DenseVector< T > &lambda_imag, DenseMatrix< T > &VR)

void	evd_left_and_right (DenseVector< T > &lambda_real, DenseVector< T > &lambda_imag, DenseMatrix< T > &VL, DenseMatrix< T > &VR)

T	det ()

unsigned int	m () const

unsigned int	n () const

void	print (std::ostream &os=libMesh::out) const

void	print_scientific (std::ostream &os, unsigned precision=8) const

template<typename T2 , typename T3 >
boostcopy::enable_if_c< ScalarTraits< T2 >::value, void >::type	add (const T2 factor, const DenseMatrixBase< T3 > &mat)

Public Attributes
bool	use_blas_lapack

Protected Member Functions
void	condense (const unsigned int i, const unsigned int j, const T val, DenseVectorBase< T > &rhs)

Static Protected Member Functions
static void	multiply (DenseMatrixBase< T > &M1, const DenseMatrixBase< T > &M2, const DenseMatrixBase< T > &M3)

Protected Attributes
unsigned int	_m

unsigned int	_n

Private Types
enum	DecompositionType { LU =0, CHOLESKY =1, LU_BLAS_LAPACK, NONE }

enum	_BLAS_Multiply_Flag { LEFT_MULTIPLY = 0, RIGHT_MULTIPLY, LEFT_MULTIPLY_TRANSPOSE, RIGHT_MULTIPLY_TRANSPOSE }

typedef PetscBLASInt	pivot_index_t

typedef int	pivot_index_t

Private Member Functions
void	_lu_decompose ()

void	_lu_back_substitute (const DenseVector< T > &b, DenseVector< T > &x) const

void	_cholesky_decompose ()

template<typename T2 >
void	_cholesky_back_substitute (const DenseVector< T2 > &b, DenseVector< T2 > &x) const

void	_multiply_blas (const DenseMatrixBase< T > &other, _BLAS_Multiply_Flag flag)

void	_lu_decompose_lapack ()

void	_svd_lapack (DenseVector< Real > &sigma)

void	_svd_lapack (DenseVector< Real > &sigma, DenseMatrix< Number > &U, DenseMatrix< Number > &VT)

void	_svd_solve_lapack (const DenseVector< T > &rhs, DenseVector< T > &x, Real rcond) const

void	_svd_helper (char JOBU, char JOBVT, std::vector< Real > &sigma_val, std::vector< Number > &U_val, std::vector< Number > &VT_val)

void	_evd_lapack (DenseVector< T > &lambda_real, DenseVector< T > &lambda_imag, DenseMatrix< T > VL=nullptr, DenseMatrix< T > VR=nullptr)

void	_lu_back_substitute_lapack (const DenseVector< T > &b, DenseVector< T > &x)

void	_matvec_blas (T alpha, T beta, DenseVector< T > &dest, const DenseVector< T > &arg, bool trans=false) const

Private Attributes
std::vector< T >	_val

DecompositionType	_decomposition_type

std::vector< pivot_index_t >	_pivots

Detailed Description

template<typename T>
class libMesh::DenseMatrix< T >

A matrix object used for finite element assembly and numerics.

Defines a dense matrix for use in Finite Element-type computations. Useful for storing element stiffness matrices before summation into a global matrix. All overridden virtual functions are documented in dense_matrix_base.h.

Author: Benjamin S. Kirk

Date: 2002

Definition at line 54 of file dense_matrix.h.

Member Typedef Documentation

◆ pivot_index_t [1/2]

template<typename T>

typedef PetscBLASInt libMesh::DenseMatrix< T >::pivot_index_t

private

Array used to store pivot indices. May be used by whatever factorization is currently active, clients of the class should not rely on it for any reason.

Definition at line 668 of file dense_matrix.h.

◆ pivot_index_t [2/2]

template<typename T>

typedef int libMesh::DenseMatrix< T >::pivot_index_t

private

Definition at line 670 of file dense_matrix.h.

Member Enumeration Documentation

◆ _BLAS_Multiply_Flag

template<typename T>

enum libMesh::DenseMatrix::_BLAS_Multiply_Flag

private

Enumeration used to determine the behavior of the _multiply_blas function.

Enumerator
LEFT_MULTIPLY
RIGHT_MULTIPLY
LEFT_MULTIPLY_TRANSPOSE
RIGHT_MULTIPLY_TRANSPOSE

Definition at line 588 of file dense_matrix.h.

                            {
     LEFT_MULTIPLY = 0,
     RIGHT_MULTIPLY,
     LEFT_MULTIPLY_TRANSPOSE,
     RIGHT_MULTIPLY_TRANSPOSE
   };

◆ DecompositionType

template<typename T>

enum libMesh::DenseMatrix::DecompositionType

private

The decomposition schemes above change the entries of the matrix A. It is therefore an error to call A.lu_solve() and subsequently call A.cholesky_solve() since the result will probably not match any desired outcome. This typedef keeps track of which decomposition has been called for this matrix.

Enumerator
LU
CHOLESKY
LU_BLAS_LAPACK
NONE

Definition at line 576 of file dense_matrix.h.

576 {LU=0, CHOLESKY=1, LU_BLAS_LAPACK, NONE};

libMesh::DenseMatrix::LU_BLAS_LAPACK

Definition: dense_matrix.h:576

libMesh::DenseMatrix::CHOLESKY

Definition: dense_matrix.h:576

libMesh::DenseMatrix::LU

Definition: dense_matrix.h:576

libMesh::DenseMatrix::NONE

Definition: dense_matrix.h:576

Constructor & Destructor Documentation

◆ DenseMatrix() [1/3]

template<typename T >

libMesh::DenseMatrix< T >::DenseMatrix	(	const unsigned int	new_m = `0`,
		const unsigned int	new_n = `0`
	)

inline

Constructor. Creates a dense matrix of dimension m by n.

Definition at line 744 of file dense_matrix.h.

                                                       :
   DenseMatrixBase<T>(new_m,new_n),
 #if defined(LIBMESH_HAVE_PETSC) && defined(LIBMESH_USE_REAL_NUMBERS) && defined(LIBMESH_DEFAULT_DOUBLE_PRECISION)
   use_blas_lapack(true),
 #else
   use_blas_lapack(false),
 #endif
   _val(),
   _decomposition_type(NONE)
 {
   this->resize(new_m,new_n);
 }

◆ DenseMatrix() [2/3]

template<typename T>

libMesh::DenseMatrix< T >::DenseMatrix ( DenseMatrix< T > && )

default

The 5 special functions can be defaulted for this class, as it does not manage any memory itself.

◆ DenseMatrix() [3/3]

template<typename T>

libMesh::DenseMatrix< T >::DenseMatrix ( const DenseMatrix< T > & )

default

◆ ~DenseMatrix()

template<typename T>

virtual libMesh::DenseMatrix< T >::~DenseMatrix ( )

virtualdefault

Member Function Documentation

◆ _cholesky_back_substitute()

template<typename T >

template<typename T2 >

void libMesh::DenseMatrix< T >::_cholesky_back_substitute	(	const DenseVector< T2 > &	b,
		DenseVector< T2 > &	x
	)		const

private

Solves the equation Ax=b for the unknown value x and rhs b based on the Cholesky factorization of A.

Note: This method may be used when A is real-valued and b and x are complex-valued.

Definition at line 1007 of file dense_matrix_impl.h.

 {
   // Shorthand notation for number of rows and columns.
   const unsigned int
     n_rows = this->m(),
     n_cols = this->n();
 
   // Just to be really sure...
   libmesh_assert_equal_to (n_rows, n_cols);
 
   // A convenient reference to *this
   const DenseMatrix<T> & A = *this;
 
   // Now compute the solution to Ax =b using the factorization.
   x.resize(n_rows);
 
   // Solve for Ly=b
   for (unsigned int i=0; i<n_cols; ++i)
     {
       T2 temp = b(i);
 
       for (unsigned int k=0; k<i; ++k)
         temp -= A(i,k)*x(k);
 
       x(i) = temp / A(i,i);
     }
 
   // Solve for L^T x = y
   for (unsigned int i=0; i<n_cols; ++i)
     {
       const unsigned int ib = (n_cols-1)-i;
 
       for (unsigned int k=(ib+1); k<n_cols; ++k)
         x(ib) -= A(k,ib) * x(k);
 
       x(ib) /= A(ib,ib);
     }
 }

◆ _cholesky_decompose()

template<typename T >

void libMesh::DenseMatrix< T >::_cholesky_decompose ( )

private

Decomposes a symmetric positive definite matrix into a product of two lower triangular matrices according to A = LL^T.

Note: This program generates an error if the matrix is not SPD.

Definition at line 961 of file dense_matrix_impl.h.

 {
   // If we called this function, there better not be any
   // previous decomposition of the matrix.
   libmesh_assert_equal_to (this->_decomposition_type, NONE);
 
   // Shorthand notation for number of rows and columns.
   const unsigned int
     n_rows = this->m(),
     n_cols = this->n();
 
   // Just to be really sure...
   libmesh_assert_equal_to (n_rows, n_cols);
 
   // A convenient reference to *this
   DenseMatrix<T> & A = *this;
 
   for (unsigned int i=0; i<n_rows; ++i)
     {
       for (unsigned int j=i; j<n_cols; ++j)
         {
           for (unsigned int k=0; k<i; ++k)
             A(i,j) -= A(i,k) * A(j,k);
 
           if (i == j)
             {
 #ifndef LIBMESH_USE_COMPLEX_NUMBERS
               if (A(i,j) <= 0.0)
                 libmesh_error_msg("Error! Can only use Cholesky decomposition with symmetric positive definite matrices.");
 #endif
 
               A(i,i) = std::sqrt(A(i,j));
             }
           else
             A(j,i) = A(i,j) / A(i,i);
         }
     }
 
   // Set the flag for CHOLESKY decomposition
   this->_decomposition_type = CHOLESKY;
 }

◆ _evd_lapack()

template<typename T>

template void libMesh::DenseMatrix< T >::_evd_lapack	(	DenseVector< T > &	lambda_real,
		DenseVector< T > &	lambda_imag,
		DenseMatrix< T > *	VL = `nullptr`,
		DenseMatrix< T > *	VR = `nullptr`
	)

private

Computes the eigenvalues of the matrix using the Lapack routine "DGEEV". If VR and/or VL are not nullptr, then the matrix of right and/or left eigenvectors is also computed and returned by this function.

[ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 703 of file dense_matrix_blas_lapack.C.

 {
   // This algorithm only works for square matrices, so verify this up front.
   if (this->m() != this->n())
     libmesh_error_msg("Can only compute eigen-decompositions for square matrices.");
 
   // If the user requests left or right eigenvectors, we have to make
   // sure and pass the transpose of this matrix to Lapack, otherwise
   // it will compute the inverse transpose of what we are
   // after... since we know the matrix is square, we can just swap
   // entries in place.  If the user does not request eigenvectors, we
   // can skip this extra step, since the eigenvalues for A and A^T are
   // the same.
   if (VL || VR)
     {
       for (auto i : IntRange<int>(0, this->_m))
         for (auto j : IntRange<int>(0, i))
           std::swap((*this)(i,j), (*this)(j,i));
     }
 
   // The calling sequence for dgeev is:
   // DGEEV (character  JOBVL,
   //        character  JOBVR,
   //        integer N,
   //        double precision, dimension( lda, * )  A,
   //        integer  LDA,
   //        double precision, dimension( * )  WR,
   //        double precision, dimension( * )  WI,
   //        double precision, dimension( ldvl, * )  VL,
   //        integer  LDVL,
   //        double precision, dimension( ldvr, * )  VR,
   //        integer  LDVR,
   //        double precision, dimension( * )  WORK,
   //        integer  LWORK,
   //        integer  INFO)
 
   // JOBVL (input)
   //       = 'N': left eigenvectors of A are not computed;
   //       = 'V': left eigenvectors of A are computed.
   char JOBVL = VL ? 'V' : 'N';
 
   // JOBVR (input)
   //       = 'N': right eigenvectors of A are not computed;
   //       = 'V': right eigenvectors of A are computed.
   char JOBVR = VR ? 'V' : 'N';
 
   // N (input)
   //   The number of rows/cols of the matrix A.  N >= 0.
   PetscBLASInt N = this->m();
 
   // A (input/output) DOUBLE PRECISION array, dimension (LDA,N)
   //   On entry, the N-by-N matrix A.
   //   On exit, A has been overwritten.
 
   // LDA (input)
   //     The leading dimension of the array A.  LDA >= max(1,N).
   PetscBLASInt LDA = N;
 
   // WR (output) double precision array, dimension (N)
   // WI (output) double precision array, dimension (N)
   //    WR and WI contain the real and imaginary parts,
   //    respectively, of the computed eigenvalues.  Complex
   //    conjugate pairs of eigenvalues appear consecutively
   //    with the eigenvalue having the positive imaginary part
   //    first.
   lambda_real.resize(N);
   lambda_imag.resize(N);
 
   // VL (output) double precision array, dimension (LDVL,N)
   //    If JOBVL = 'V', the left eigenvectors u(j) are stored one
   //    after another in the columns of VL, in the same order
   //    as their eigenvalues.
   //    If JOBVL = 'N', VL is not referenced.
   //    If the j-th eigenvalue is real, then u(j) = VL(:,j),
   //    the j-th column of VL.
   //    If the j-th and (j+1)-st eigenvalues form a complex
   //    conjugate pair, then u(j) = VL(:,j) + i*VL(:,j+1) and
   //    u(j+1) = VL(:,j) - i*VL(:,j+1).
   // Will be set below if needed.
 
   // LDVL (input)
   //      The leading dimension of the array VL.  LDVL >= 1; if
   //      JOBVL = 'V', LDVL >= N.
   PetscBLASInt LDVL = VL ? N : 1;
 
   // VR (output) DOUBLE PRECISION array, dimension (LDVR,N)
   //    If JOBVR = 'V', the right eigenvectors v(j) are stored one
   //    after another in the columns of VR, in the same order
   //    as their eigenvalues.
   //    If JOBVR = 'N', VR is not referenced.
   //    If the j-th eigenvalue is real, then v(j) = VR(:,j),
   //    the j-th column of VR.
   //    If the j-th and (j+1)-st eigenvalues form a complex
   //    conjugate pair, then v(j) = VR(:,j) + i*VR(:,j+1) and
   //    v(j+1) = VR(:,j) - i*VR(:,j+1).
   // Will be set below if needed.
 
   // LDVR (input)
   //      The leading dimension of the array VR.  LDVR >= 1; if
   //      JOBVR = 'V', LDVR >= N.
   PetscBLASInt LDVR = VR ? N : 1;
 
   // WORK (workspace/output) double precision array, dimension (MAX(1,LWORK))
   //      On exit, if INFO = 0, WORK(1) returns the optimal LWORK.
   //
   // LWORK (input)
   //       The dimension of the array WORK.  LWORK >= max(1,3*N), and
   //       if JOBVL = 'V' or JOBVR = 'V', LWORK >= 4*N.  For good
   //       performance, LWORK must generally be larger.
   //
   //       If LWORK = -1, then a workspace query is assumed; the routine
   //       only calculates the optimal size of the WORK array, returns
   //       this value as the first entry of the WORK array, and no error
   //       message related to LWORK is issued by XERBLA.
   PetscBLASInt LWORK = (VR || VL) ? 4*N : 3*N;
   std::vector<T> WORK(LWORK);
 
   // INFO (output)
   //      = 0:  successful exit
   //      < 0:  if INFO = -i, the i-th argument had an illegal value.
   //      > 0:  if INFO = i, the QR algorithm failed to compute all the
   //            eigenvalues, and no eigenvectors or condition numbers
   //            have been computed; elements 1:ILO-1 and i+1:N of WR
   //            and WI contain eigenvalues which have converged.
   PetscBLASInt INFO = 0;
 
   // Get references to raw data
   std::vector<T> & lambda_real_val = lambda_real.get_values();
   std::vector<T> & lambda_imag_val = lambda_imag.get_values();
 
   // Set up eigenvector storage if necessary.
   T * VR_ptr = nullptr;
   if (VR)
     {
       VR->resize(N, N);
       VR_ptr = VR->get_values().data();
     }
 
   T * VL_ptr = nullptr;
   if (VL)
     {
       VL->resize(N, N);
       VL_ptr = VL->get_values().data();
     }
 
   // Ready to call the Lapack routine through PETSc's interface
   LAPACKgeev_(&JOBVL,
               &JOBVR,
               &N,
               _val.data(),
               &LDA,
               lambda_real_val.data(),
               lambda_imag_val.data(),
               VL_ptr,
               &LDVL,
               VR_ptr,
               &LDVR,
               WORK.data(),
               &LWORK,
               &INFO);
 
   // Check return value for errors
   if (INFO != 0)
     libmesh_error_msg("INFO=" << INFO << ", Error during Lapack eigenvalue calculation!");
 
   // If the user requested either right or left eigenvectors, LAPACK
   // has now computed the transpose of the desired matrix, i.e. V^T
   // instead of V.  We could leave this up to user code to handle, but
   // rather than risking getting very unexpected results, we'll just
   // transpose it in place before handing it back.
   if (VR)
     {
       for (auto i : IntRange<int>(0, N))
         for (auto j : IntRange<int>(0, i))
           std::swap((*VR)(i,j), (*VR)(j,i));
     }
 
   if (VL)
     {
       for (auto i : IntRange<int>(0, N))
         for (auto j : IntRange<int>(0, i))
           std::swap((*VL)(i,j), (*VL)(j,i));
     }
 }

◆ _lu_back_substitute()

template<typename T>

void libMesh::DenseMatrix< T >::_lu_back_substitute	(	const DenseVector< T > &	b,
		DenseVector< T > &	x
	)		const

private

Solves the system Ax=b through back substitution. This function is private since it is only called as part of the implementation of the lu_solve(...) function.

Definition at line 666 of file dense_matrix_impl.h.

 {
   const unsigned int
     n_cols = this->n();
 
   libmesh_assert_equal_to (this->m(), n_cols);
   libmesh_assert_equal_to (this->m(), b.size());
 
   x.resize (n_cols);
 
   // A convenient reference to *this
   const DenseMatrix<T> & A = *this;
 
   // Temporary vector storage.  We use this instead of
   // modifying the RHS.
   DenseVector<T> z = b;
 
   // Lower-triangular "top to bottom" solve step, taking into account pivots
   for (unsigned int i=0; i<n_cols; ++i)
     {
       // Swap
       if (_pivots[i] != static_cast<pivot_index_t>(i))
         std::swap( z(i), z(_pivots[i]) );
 
       x(i) = z(i);
 
       for (unsigned int j=0; j<i; ++j)
         x(i) -= A(i,j)*x(j);
 
       x(i) /= A(i,i);
     }
 
   // Upper-triangular "bottom to top" solve step
   const unsigned int last_row = n_cols-1;
 
   for (int i=last_row; i>=0; --i)
     {
       for (int j=i+1; j<static_cast<int>(n_cols); ++j)
         x(i) -= A(i,j)*x(j);
     }
 }

◆ _lu_back_substitute_lapack()

template<typename T>

template void libMesh::DenseMatrix< T >::_lu_back_substitute_lapack	(	const DenseVector< T > &	b,
		DenseVector< T > &	x
	)

private

Companion function to _lu_decompose_lapack(). Do not use directly, called through the public lu_solve() interface. This function is logically const in that it does not modify the matrix, but since we are just calling LAPACK routines, it's less const_cast hassle to just declare the function non-const. [ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 911 of file dense_matrix_blas_lapack.C.

 {
   // The calling sequence for getrs is:
   // dgetrs(TRANS, N, NRHS, A, LDA, IPIV, B, LDB, INFO)
 
   // trans (input)
   //       'n' for no transpose, 't' for transpose
   char TRANS[] = "t";
 
   // N (input)
   //   The order of the matrix A.  N >= 0.
   PetscBLASInt N = this->m();
 
 
   // NRHS (input)
   //      The number of right hand sides, i.e., the number of columns
   //      of the matrix B.  NRHS >= 0.
   PetscBLASInt NRHS = 1;
 
   // A (input) double precision array, dimension (LDA,N)
   //   The factors L and U from the factorization A = P*L*U
   //   as computed by dgetrf.
 
   // LDA (input)
   //     The leading dimension of the array A.  LDA >= max(1,N).
   PetscBLASInt LDA = N;
 
   // ipiv (input) int array, dimension (N)
   //      The pivot indices from DGETRF; for 1<=i<=N, row i of the
   //      matrix was interchanged with row IPIV(i).
   // Here, we pass _pivots.data() which was computed in _lu_decompose_lapack
 
   // B (input/output) double precision array, dimension (LDB,NRHS)
   //   On entry, the right hand side matrix B.
   //   On exit, the solution matrix X.
   // Here, we pass a copy of the rhs vector's data array in x, so that the
   // passed right-hand side b is unmodified.  I don't see a way around this
   // copy if we want to maintain an unmodified rhs in LibMesh.
   x = b;
   std::vector<T> & x_vec = x.get_values();
 
   // We can avoid the copy if we don't care about overwriting the RHS: just
   // pass b to the Lapack routine and then swap with x before exiting
   // std::vector<T> & x_vec = b.get_values();
 
   // LDB (input)
   //     The leading dimension of the array B.  LDB >= max(1,N).
   PetscBLASInt LDB = N;
 
   // INFO (output)
   //      = 0:  successful exit
   //      < 0:  if INFO = -i, the i-th argument had an illegal value
   PetscBLASInt INFO = 0;
 
   // Finally, ready to call the Lapack getrs function
   LAPACKgetrs_(TRANS, &N, &NRHS, _val.data(), &LDA, _pivots.data(), x_vec.data(), &LDB, &INFO);
 
   // Check return value for errors
   if (INFO != 0)
     libmesh_error_msg("INFO=" << INFO << ", Error during Lapack LU solve!");
 
   // Don't do this if you already made a copy of b above
   // Swap b and x.  The solution will then be in x, and whatever was originally
   // in x, maybe garbage, maybe nothing, will be in b.
   // FIXME: Rewrite the LU and Cholesky solves to just take one input, and overwrite
   // the input.  This *should* make user code simpler, as they don't have to create
   // an extra vector just to pass it in to the solve function!
   // b.swap(x);
 }

◆ _lu_decompose()

template<typename T >

void libMesh::DenseMatrix< T >::_lu_decompose ( )

private

Form the LU decomposition of the matrix. This function is private since it is only called as part of the implementation of the lu_solve(...) function.

Definition at line 717 of file dense_matrix_impl.h.

 {
   // If this function was called, there better not be any
   // previous decomposition of the matrix.
   libmesh_assert_equal_to (this->_decomposition_type, NONE);
 
   // Get the matrix size and make sure it is square
   const unsigned int
     n_rows = this->m();
 
   // A convenient reference to *this
   DenseMatrix<T> & A = *this;
 
   _pivots.resize(n_rows);
 
   for (unsigned int i=0; i<n_rows; ++i)
     {
       // Find the pivot row by searching down the i'th column
       _pivots[i] = i;
 
       // std::abs(complex) must return a Real!
       Real the_max = std::abs( A(i,i) );
       for (unsigned int j=i+1; j<n_rows; ++j)
         {
           Real candidate_max = std::abs( A(j,i) );
           if (the_max < candidate_max)
             {
               the_max = candidate_max;
               _pivots[i] = j;
             }
         }
 
       // libMesh::out << "the_max=" << the_max << " found at row " << _pivots[i] << std::endl;
 
       // If the max was found in a different row, interchange rows.
       // Here we interchange the *entire* row, in Gaussian elimination
       // you would only interchange the subrows A(i,j) and A(p(i),j), for j>i
       if (_pivots[i] != static_cast<pivot_index_t>(i))
         {
           for (unsigned int j=0; j<n_rows; ++j)
             std::swap( A(i,j), A(_pivots[i], j) );
         }
 
 
       // If the max abs entry found is zero, the matrix is singular
       if (A(i,i) == libMesh::zero)
         libmesh_error_msg("Matrix A is singular!");
 
       // Scale upper triangle entries of row i by the diagonal entry
       // Note: don't scale the diagonal entry itself!
       const T diag_inv = 1. / A(i,i);
       for (unsigned int j=i+1; j<n_rows; ++j)
         A(i,j) *= diag_inv;
 
       // Update the remaining sub-matrix A[i+1:m][i+1:m]
       // by subtracting off (the diagonal-scaled)
       // upper-triangular part of row i, scaled by the
       // i'th column entry of each row.  In terms of
       // row operations, this is:
       // for each r > i
       //   SubRow(r) = SubRow(r) - A(r,i)*SubRow(i)
       //
       // If we were scaling the i'th column as well, like
       // in Gaussian elimination, this would 'zero' the
       // entry in the i'th column.
       for (unsigned int row=i+1; row<n_rows; ++row)
         for (unsigned int col=i+1; col<n_rows; ++col)
           A(row,col) -= A(row,i) * A(i,col);
 
     } // end i loop
 
   // Set the flag for LU decomposition
   this->_decomposition_type = LU;
 }

◆ _lu_decompose_lapack()

template<typename T >

template void libMesh::DenseMatrix< T >::_lu_decompose_lapack ( )

private

Computes an LU factorization of the matrix using the Lapack routine "getrf". This routine should only be used by the "use_blas_lapack" branch of the lu_solve() function. After the call to this function, the matrix is replaced by its factorized version, and the DecompositionType is set to LU_BLAS_LAPACK. [ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 207 of file dense_matrix_blas_lapack.C.

 {
   // If this function was called, there better not be any
   // previous decomposition of the matrix.
   libmesh_assert_equal_to (this->_decomposition_type, NONE);
 
   // The calling sequence for dgetrf is:
   // dgetrf(M, N, A, lda, ipiv, info)
 
   // M (input)
   //   The number of rows of the matrix A.  M >= 0.
   // In C/C++, pass the number of *cols* of A
   PetscBLASInt M = this->n();
 
   // N (input)
   //   The number of columns of the matrix A.  N >= 0.
   // In C/C++, pass the number of *rows* of A
   PetscBLASInt N = this->m();
 
   // A (input/output) double precision array, dimension (LDA,N)
   //   On entry, the M-by-N matrix to be factored.
   //   On exit, the factors L and U from the factorization
   //   A = P*L*U; the unit diagonal elements of L are not stored.
 
   // LDA (input)
   //     The leading dimension of the array A.  LDA >= max(1,M).
   PetscBLASInt LDA = M;
 
   // ipiv (output) integer array, dimension (min(m,n))
   //      The pivot indices; for 1 <= i <= min(m,n), row i of the
   //      matrix was interchanged with row IPIV(i).
   // Here, we pass _pivots.data(), a private class member used to store pivots
   this->_pivots.resize( std::min(M,N) );
 
   // info (output)
   //      = 0:  successful exit
   //      < 0:  if INFO = -i, the i-th argument had an illegal value
   //      > 0:  if INFO = i, U(i,i) is exactly zero. The factorization
   //            has been completed, but the factor U is exactly
   //            singular, and division by zero will occur if it is used
   //            to solve a system of equations.
   PetscBLASInt INFO = 0;
 
   // Ready to call the actual factorization routine through PETSc's interface
   LAPACKgetrf_(&M, &N, this->_val.data(), &LDA, _pivots.data(), &INFO);
 
   // Check return value for errors
   if (INFO != 0)
     libmesh_error_msg("INFO=" << INFO << ", Error during Lapack LU factorization!");
 
   // Set the flag for LU decomposition
   this->_decomposition_type = LU_BLAS_LAPACK;
 }

◆ _matvec_blas()

template<typename T>

template void libMesh::DenseMatrix< T >::_matvec_blas	(	T	alpha,
		T	beta,
		DenseVector< T > &	dest,
		const DenseVector< T > &	arg,
		bool	trans = `false`
	)		const

private

Uses the BLAS GEMV function (through PETSc) to compute

dest := alpha*A*arg + beta*dest

where alpha and beta are scalars, A is this matrix, and arg and dest are input vectors of appropriate size. If trans is true, the transpose matvec is computed instead. By default, trans==false.

[ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 1000 of file dense_matrix_blas_lapack.C.

 {
   // Ensure that dest and arg sizes are compatible
   if (!trans)
     {
       // dest  ~ A     * arg
       // (mx1)   (mxn) * (nx1)
       if ((dest.size() != this->m()) || (arg.size() != this->n()))
         libmesh_error_msg("Improper input argument sizes!");
     }
 
   else // trans == true
     {
       // Ensure that dest and arg are proper size
       // dest  ~ A^T   * arg
       // (nx1)   (nxm) * (mx1)
       if ((dest.size() != this->n()) || (arg.size() != this->m()))
         libmesh_error_msg("Improper input argument sizes!");
     }
 
   // Calling sequence for dgemv:
   //
   // dgemv(TRANS,M,N,ALPHA,A,LDA,X,INCX,BETA,Y,INCY)
 
   // TRANS (input)
   //       't' for transpose, 'n' for non-transpose multiply
   // We store everything in row-major order, so pass the transpose flag for
   // non-transposed matvecs and the 'n' flag for transposed matvecs
   char TRANS[] = "t";
   if (trans)
     TRANS[0] = 'n';
 
   // M (input)
   //   On entry, M specifies the number of rows of the matrix A.
   // In C/C++, pass the number of *cols* of A
   PetscBLASInt M = this->n();
 
   // N (input)
   //   On entry, N specifies the number of columns of the matrix A.
   // In C/C++, pass the number of *rows* of A
   PetscBLASInt N = this->m();
 
   // ALPHA (input)
   // The scalar constant passed to this function
 
   // A (input) double precision array of DIMENSION ( LDA, n ).
   //   Before entry, the leading m by n part of the array A must
   //   contain the matrix of coefficients.
   // The matrix, *this.  Note that _matvec_blas is called from
   // a const function, vector_mult(), and so we have made this function const
   // as well.  Since BLAS knows nothing about const, we have to cast it away
   // now.
   DenseMatrix<T> & a_ref = const_cast<DenseMatrix<T> &> ( *this );
   std::vector<T> & a = a_ref.get_values();
 
   // LDA (input)
   //     On entry, LDA specifies the first dimension of A as declared
   //     in the calling (sub) program. LDA must be at least
   //     max( 1, m ).
   PetscBLASInt LDA = M;
 
   // X (input) double precision array of DIMENSION at least
   //   ( 1 + ( n - 1 )*abs( INCX ) ) when TRANS = 'N' or 'n'
   //   and at least
   //   ( 1 + ( m - 1 )*abs( INCX ) ) otherwise.
   //   Before entry, the incremented array X must contain the
   //   vector x.
   // Here, we must cast away the const-ness of "arg" since BLAS knows
   // nothing about const
   DenseVector<T> & x_ref = const_cast<DenseVector<T> &> ( arg );
   std::vector<T> & x = x_ref.get_values();
 
   // INCX (input)
   //      On entry, INCX specifies the increment for the elements of
   //      X. INCX must not be zero.
   PetscBLASInt INCX = 1;
 
   // BETA (input)
   //      On entry, BETA specifies the scalar beta. When BETA is
   //      supplied as zero then Y need not be set on input.
   // The second scalar constant passed to this function
 
   // Y (input) double precision array of DIMENSION at least
   //   ( 1 + ( m - 1 )*abs( INCY ) ) when TRANS = 'N' or 'n'
   //   and at least
   //   ( 1 + ( n - 1 )*abs( INCY ) ) otherwise.
   //   Before entry with BETA non-zero, the incremented array Y
   //   must contain the vector y. On exit, Y is overwritten by the
   //   updated vector y.
   // The input vector "dest"
   std::vector<T> & y = dest.get_values();
 
   // INCY (input)
   //      On entry, INCY specifies the increment for the elements of
   //      Y. INCY must not be zero.
   PetscBLASInt INCY = 1;
 
   // Finally, ready to call the BLAS function
   BLASgemv_(TRANS, &M, &N, &alpha, a.data(), &LDA, x.data(), &INCX, &beta, y.data(), &INCY);
 }

◆ _multiply_blas()

template<typename T>

template void libMesh::DenseMatrix< T >::_multiply_blas	(	const DenseMatrixBase< T > &	other,
		_BLAS_Multiply_Flag	flag
	)

private

The _multiply_blas function computes A <- op(A) * op(B) using BLAS gemm function. Used in the right_multiply(), left_multiply(), right_multiply_transpose(), and left_multiply_transpose() routines. [ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 37 of file dense_matrix_blas_lapack.C.

 {
   int result_size = 0;
 
   // For each case, determine the size of the final result make sure
   // that the inner dimensions match
   switch (flag)
     {
     case LEFT_MULTIPLY:
       {
         result_size = other.m() * this->n();
         if (other.n() == this->m())
           break;
       }
       libmesh_fallthrough();
     case RIGHT_MULTIPLY:
       {
         result_size = other.n() * this->m();
         if (other.m() == this->n())
           break;
       }
       libmesh_fallthrough();
     case LEFT_MULTIPLY_TRANSPOSE:
       {
         result_size = other.n() * this->n();
         if (other.m() == this->m())
           break;
       }
       libmesh_fallthrough();
     case RIGHT_MULTIPLY_TRANSPOSE:
       {
         result_size = other.m() * this->m();
         if (other.n() == this->n())
           break;
       }
       libmesh_fallthrough();
     default:
       libmesh_error_msg("Unknown flag selected or matrices are incompatible for multiplication.");
     }
 
   // For this to work, the passed arg. must actually be a DenseMatrix<T>
   const DenseMatrix<T> * const_that = cast_ptr<const DenseMatrix<T> *>(&other);
 
   // Also, although 'that' is logically const in this BLAS routine,
   // the PETSc BLAS interface does not specify that any of the inputs are
   // const.  To use it, I must cast away const-ness.
   DenseMatrix<T> * that = const_cast<DenseMatrix<T> *> (const_that);
 
   // Initialize A, B pointers for LEFT_MULTIPLY* cases
   DenseMatrix<T> * A = this;
   DenseMatrix<T> * B = that;
 
   // For RIGHT_MULTIPLY* cases, swap the meaning of A and B.
   // Here is a full table of combinations we can pass to BLASgemm, and what the answer is when finished:
   // pass A B   -> (Fortran) -> A^T B^T -> (C++) -> (A^T B^T)^T -> (identity) -> B A   "lt multiply"
   // pass B A   -> (Fortran) -> B^T A^T -> (C++) -> (B^T A^T)^T -> (identity) -> A B   "rt multiply"
   // pass A B^T -> (Fortran) -> A^T B   -> (C++) -> (A^T B)^T   -> (identity) -> B^T A "lt multiply t"
   // pass B^T A -> (Fortran) -> B A^T   -> (C++) -> (B A^T)^T   -> (identity) -> A B^T "rt multiply t"
   if (flag==RIGHT_MULTIPLY || flag==RIGHT_MULTIPLY_TRANSPOSE)
     std::swap(A,B);
 
   // transa, transb values to pass to blas
   char
     transa[] = "n",
     transb[] = "n";
 
   // Integer values to pass to BLAS:
   //
   // M
   // In Fortran, the number of rows of op(A),
   // In the BLAS documentation, typically known as 'M'.
   //
   // In C/C++, we set:
   // M = n_cols(A) if (transa='n')
   //     n_rows(A) if (transa='t')
   PetscBLASInt M = static_cast<PetscBLASInt>( A->n() );
 
   // N
   // In Fortran, the number of cols of op(B), and also the number of cols of C.
   // In the BLAS documentation, typically known as 'N'.
   //
   // In C/C++, we set:
   // N = n_rows(B) if (transb='n')
   //     n_cols(B) if (transb='t')
   PetscBLASInt N = static_cast<PetscBLASInt>( B->m() );
 
   // K
   // In Fortran, the number of cols of op(A), and also
   // the number of rows of op(B). In the BLAS documentation,
   // typically known as 'K'.
   //
   // In C/C++, we set:
   // K = n_rows(A) if (transa='n')
   //     n_cols(A) if (transa='t')
   PetscBLASInt K = static_cast<PetscBLASInt>( A->m() );
 
   // LDA (leading dimension of A). In our cases,
   // LDA is always the number of columns of A.
   PetscBLASInt LDA = static_cast<PetscBLASInt>( A->n() );
 
   // LDB (leading dimension of B).  In our cases,
   // LDB is always the number of columns of B.
   PetscBLASInt LDB = static_cast<PetscBLASInt>( B->n() );
 
   if (flag == LEFT_MULTIPLY_TRANSPOSE)
     {
       transb[0] = 't';
       N = static_cast<PetscBLASInt>( B->n() );
     }
 
   else if (flag == RIGHT_MULTIPLY_TRANSPOSE)
     {
       transa[0] = 't';
       std::swap(M,K);
     }
 
   // LDC (leading dimension of C).  LDC is the
   // number of columns in the solution matrix.
   PetscBLASInt LDC = M;
 
   // Scalar values to pass to BLAS
   //
   // scalar multiplying the whole product AB
   T alpha = 1.;
 
   // scalar multiplying C, which is the original matrix.
   T beta  = 0.;
 
   // Storage for the result
   std::vector<T> result (result_size);
 
   // Finally ready to call the BLAS
   BLASgemm_(transa, transb, &M, &N, &K, &alpha, A->get_values().data(), &LDA, B->get_values().data(), &LDB, &beta, result.data(), &LDC);
 
   // Update the relevant dimension for this matrix.
   switch (flag)
     {
     case LEFT_MULTIPLY:            { this->_m = other.m(); break; }
     case RIGHT_MULTIPLY:           { this->_n = other.n(); break; }
     case LEFT_MULTIPLY_TRANSPOSE:  { this->_m = other.n(); break; }
     case RIGHT_MULTIPLY_TRANSPOSE: { this->_n = other.m(); break; }
     default:
       libmesh_error_msg("Unknown flag selected.");
     }
 
   // Swap my data vector with the result
   this->_val.swap(result);
 }

◆ _svd_helper()

template<typename T >

template void libMesh::DenseMatrix< T >::_svd_helper	(	char	JOBU,
		char	JOBVT,
		std::vector< Real > &	sigma_val,
		std::vector< Number > &	U_val,
		std::vector< Number > &	VT_val
	)

private

Helper function that actually performs the SVD. [ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 381 of file dense_matrix_blas_lapack.C.

 {
 
   // M (input)
   //   The number of rows of the matrix A.  M >= 0.
   // In C/C++, pass the number of *cols* of A
   PetscBLASInt M = this->n();
 
   // N (input)
   //   The number of columns of the matrix A.  N >= 0.
   // In C/C++, pass the number of *rows* of A
   PetscBLASInt N = this->m();
 
   PetscBLASInt min_MN = (M < N) ? M : N;
   PetscBLASInt max_MN = (M > N) ? M : N;
 
   // A (input/output) DOUBLE PRECISION array, dimension (LDA,N)
   //   On entry, the M-by-N matrix A.
   //   On exit,
   //   if JOBU  = 'O', A is overwritten with the first min(m,n)
   //                   columns of U (the left singular vectors,
   //                   stored columnwise);
   //   if JOBVT = 'O', A is overwritten with the first min(m,n)
   //                   rows of V**T (the right singular vectors,
   //                   stored rowwise);
   //   if JOBU != 'O' and JOBVT != 'O', the contents of A are destroyed.
 
   // LDA (input)
   //     The leading dimension of the array A.  LDA >= max(1,M).
   PetscBLASInt LDA = M;
 
   // S (output) DOUBLE PRECISION array, dimension (min(M,N))
   //   The singular values of A, sorted so that S(i) >= S(i+1).
   sigma_val.resize( min_MN );
 
   // LDU (input)
   //     The leading dimension of the array U.  LDU >= 1; if
   //     JOBU = 'S' or 'A', LDU >= M.
   PetscBLASInt LDU = M;
 
   // U (output) DOUBLE PRECISION array, dimension (LDU,UCOL)
   //   (LDU,M) if JOBU = 'A' or (LDU,min(M,N)) if JOBU = 'S'.
   //   If JOBU = 'A', U contains the M-by-M orthogonal matrix U;
   //   if JOBU = 'S', U contains the first min(m,n) columns of U
   //   (the left singular vectors, stored columnwise);
   //   if JOBU = 'N' or 'O', U is not referenced.
   if (JOBU == 'S')
     U_val.resize( LDU*min_MN );
   else
     U_val.resize( LDU*M );
 
   // LDVT (input)
   //      The leading dimension of the array VT.  LDVT >= 1; if
   //      JOBVT = 'A', LDVT >= N; if JOBVT = 'S', LDVT >= min(M,N).
   PetscBLASInt LDVT = N;
   if (JOBVT == 'S')
     LDVT = min_MN;
 
   // VT (output) DOUBLE PRECISION array, dimension (LDVT,N)
   //    If JOBVT = 'A', VT contains the N-by-N orthogonal matrix
   //    V**T;
   //    if JOBVT = 'S', VT contains the first min(m,n) rows of
   //    V**T (the right singular vectors, stored rowwise);
   //    if JOBVT = 'N' or 'O', VT is not referenced.
   VT_val.resize( LDVT*N );
 
   // LWORK (input)
   //       The dimension of the array WORK.
   //       LWORK >= MAX(1,3*MIN(M,N)+MAX(M,N),5*MIN(M,N)).
   //       For good performance, LWORK should generally be larger.
   //
   //       If LWORK = -1, then a workspace query is assumed; the routine
   //       only calculates the optimal size of the WORK array, returns
   //       this value as the first entry of the WORK array, and no error
   //       message related to LWORK is issued by XERBLA.
   PetscBLASInt larger = (3*min_MN+max_MN > 5*min_MN) ? 3*min_MN+max_MN : 5*min_MN;
   PetscBLASInt LWORK  = (larger > 1) ? larger : 1;
 
 
   // WORK (workspace/output) DOUBLE PRECISION array, dimension (MAX(1,LWORK))
   //      On exit, if INFO = 0, WORK(1) returns the optimal LWORK;
   //      if INFO > 0, WORK(2:MIN(M,N)) contains the unconverged
   //      superdiagonal elements of an upper bidiagonal matrix B
   //      whose diagonal is in S (not necessarily sorted). B
   //      satisfies A = U * B * VT, so it has the same singular values
   //      as A, and singular vectors related by U and VT.
   std::vector<Number> WORK( LWORK );
 
   // INFO (output)
   //      = 0:  successful exit.
   //      < 0:  if INFO = -i, the i-th argument had an illegal value.
   //      > 0:  if DBDSQR did not converge, INFO specifies how many
   //            superdiagonals of an intermediate bidiagonal form B
   //            did not converge to zero. See the description of WORK
   //            above for details.
   PetscBLASInt INFO = 0;
 
   // Ready to call the actual factorization routine through PETSc's interface.
 #ifdef LIBMESH_USE_REAL_NUMBERS
   // Note that the call to LAPACKgesvd_ may modify _val
   LAPACKgesvd_(&JOBU, &JOBVT, &M, &N, _val.data(), &LDA, sigma_val.data(), U_val.data(),
                &LDU, VT_val.data(), &LDVT, WORK.data(), &LWORK, &INFO);
 #else
   // When we have LIBMESH_USE_COMPLEX_NUMBERS then we must pass an array of Complex
   // numbers to LAPACKgesvd_, but _val may contain Reals so we copy to Number below to
   // handle both the real-valued and complex-valued cases.
   std::vector<Number> val_copy(_val.size());
   for (std::size_t i=0; i<_val.size(); i++)
     val_copy[i] = _val[i];
 
   std::vector<Real> RWORK(5 * min_MN);
   LAPACKgesvd_(&JOBU, &JOBVT, &M, &N, val_copy.data(), &LDA, sigma_val.data(), U_val.data(),
                &LDU, VT_val.data(), &LDVT, WORK.data(), &LWORK, RWORK.data(), &INFO);
 #endif
 
   // Check return value for errors
   if (INFO != 0)
     libmesh_error_msg("INFO=" << INFO << ", Error during Lapack SVD calculation!");
 }

◆ _svd_lapack() [1/2]

template<typename T >

template void libMesh::DenseMatrix< T >::_svd_lapack ( DenseVector< Real > & sigma )

private

Computes an SVD of the matrix using the Lapack routine "getsvd". [ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 274 of file dense_matrix_blas_lapack.C.

 {
   // The calling sequence for dgetrf is:
   // DGESVD( JOBU, JOBVT, M, N, A, LDA, S, U, LDU, VT, LDVT, WORK, LWORK, INFO )
 
   // JOBU (input)
   //      Specifies options for computing all or part of the matrix U:
   //      = 'A':  all M columns of U are returned in array U:
   //      = 'S':  the first min(m,n) columns of U (the left singular
   //              vectors) are returned in the array U;
   //      = 'O':  the first min(m,n) columns of U (the left singular
   //              vectors) are overwritten on the array A;
   //      = 'N':  no columns of U (no left singular vectors) are
   //              computed.
   char JOBU = 'N';
 
   // JOBVT (input)
   //       Specifies options for computing all or part of the matrix
   //       V**T:
   //       = 'A':  all N rows of V**T are returned in the array VT;
   //       = 'S':  the first min(m,n) rows of V**T (the right singular
   //               vectors) are returned in the array VT;
   //       = 'O':  the first min(m,n) rows of V**T (the right singular
   //               vectors) are overwritten on the array A;
   //       = 'N':  no rows of V**T (no right singular vectors) are
   //               computed.
   char JOBVT = 'N';
 
   std::vector<Real> sigma_val;
   std::vector<Number> U_val;
   std::vector<Number> VT_val;
 
   _svd_helper(JOBU, JOBVT, sigma_val, U_val, VT_val);
 
   // Copy the singular values into sigma, ignore U_val and VT_val
   sigma.resize(cast_int<unsigned int>(sigma_val.size()));
   for (auto i : IntRange<int>(0, sigma.size()))
     sigma(i) = sigma_val[i];
 }

◆ _svd_lapack() [2/2]

template<typename T >

template void libMesh::DenseMatrix< T >::_svd_lapack	(	DenseVector< Real > &	sigma,
		DenseMatrix< Number > &	U,
		DenseMatrix< Number > &	VT
	)

private

Computes a "reduced" SVD of the matrix using the Lapack routine "getsvd". [ Implementation in dense_matrix_blas_lapack.C ]

Definition at line 315 of file dense_matrix_blas_lapack.C.

 {
   // The calling sequence for dgetrf is:
   // DGESVD( JOBU, JOBVT, M, N, A, LDA, S, U, LDU, VT, LDVT, WORK, LWORK, INFO )
 
   // JOBU (input)
   //      Specifies options for computing all or part of the matrix U:
   //      = 'A':  all M columns of U are returned in array U:
   //      = 'S':  the first min(m,n) columns of U (the left singular
   //              vectors) are returned in the array U;
   //      = 'O':  the first min(m,n) columns of U (the left singular
   //              vectors) are overwritten on the array A;
   //      = 'N':  no columns of U (no left singular vectors) are
   //              computed.
   char JOBU = 'S';
 
   // JOBVT (input)
   //       Specifies options for computing all or part of the matrix
   //       V**T:
   //       = 'A':  all N rows of V**T are returned in the array VT;
   //       = 'S':  the first min(m,n) rows of V**T (the right singular
   //               vectors) are returned in the array VT;
   //       = 'O':  the first min(m,n) rows of V**T (the right singular
   //               vectors) are overwritten on the array A;
   //       = 'N':  no rows of V**T (no right singular vectors) are
   //               computed.
   char JOBVT = 'S';
 
   // Note: Lapack is going to compute the singular values of A^T.  If
   // A=U * S * V^T, then A^T = V * S * U^T, which means that the
   // values returned in the "U_val" array actually correspond to the
   // entries of the V matrix, and the values returned in the VT_val
   // array actually correspond to the entries of U^T.  Therefore, we
   // pass VT in the place of U and U in the place of VT below!
   std::vector<Real> sigma_val;
   int M = this->n();
   int N = this->m();
   int min_MN = (M < N) ? M : N;
 
   // Size user-provided storage appropriately. Inside svd_helper:
   // U_val is sized to (M x min_MN)
   // VT_val is sized to (min_MN x N)
   // So, we set up U to have the shape of "VT_val^T", and VT to
   // have the shape of "U_val^T".
   //
   // Finally, since the results are stored in column-major order by
   // Lapack, but we actually want the transpose of what Lapack
   // returns, this means (conveniently) that we don't even have to
   // copy anything after the call to _svd_helper, it should already be
   // in the correct order!
   U.resize(N, min_MN);
   VT.resize(min_MN, M);
 
   _svd_helper(JOBU, JOBVT, sigma_val, VT.get_values(), U.get_values());
 
   // Copy the singular values into sigma.
   sigma.resize(cast_int<unsigned int>(sigma_val.size()));
   for (auto i : IntRange<int>(0, sigma.size()))
     sigma(i) = sigma_val[i];
 }

◆ _svd_solve_lapack()

template<typename T>

template void libMesh::DenseMatrix< T >::_svd_solve_lapack	(	const DenseVector< T > &	rhs,
		DenseVector< T > &	x,
		Real	rcond
	)		const

private

Called by svd_solve(rhs).

Definition at line 526 of file dense_matrix_blas_lapack.C.

 {
   // Since BLAS is expecting column-major storage, we first need to
   // make a transposed copy of *this, then pass it to the gelss
   // routine instead of the original.  This extra copy is kind of a
   // bummer, it might be better if we could use the full SVD to
   // compute the least-squares solution instead...  Note that it isn't
   // completely terrible either, since A_trans gets overwritten by
   // Lapack, and we usually would end up making a copy of A outside
   // the function call anyway.
   DenseMatrix<T> A_trans;
   this->get_transpose(A_trans);
 
   // M
   // The number of rows of the input matrix. M >= 0.
   // This is actually the number of *columns* of A_trans.
   PetscBLASInt M = A_trans.n();
 
   // N
   // The number of columns of the matrix A. N >= 0.
   // This is actually the number of *rows* of A_trans.
   PetscBLASInt N = A_trans.m();
 
   // We'll use the min and max of (M,N) several times below.
   PetscBLASInt max_MN = std::max(M,N);
   PetscBLASInt min_MN = std::min(M,N);
 
   // NRHS
   // The number of right hand sides, i.e., the number of columns
   // of the matrices B and X. NRHS >= 0.
   // This could later be generalized to solve for multiple right-hand
   // sides...
   PetscBLASInt NRHS = 1;
 
   // A is double precision array, dimension (LDA,N)
   // On entry, the M-by-N matrix A.
   // On exit, the first min(m,n) rows of A are overwritten with
   // its right singular vectors, stored rowwise.
   //
   // The data vector that will be passed to Lapack.
   std::vector<T> & A_trans_vals = A_trans.get_values();
 
   // LDA
   // The leading dimension of the array A.  LDA >= max(1,M).
   PetscBLASInt LDA = M;
 
   // B is double precision array, dimension (LDB,NRHS)
   // On entry, the M-by-NRHS right hand side matrix B.
   // On exit, B is overwritten by the N-by-NRHS solution
   // matrix X.  If m >= n and RANK = n, the residual
   // sum-of-squares for the solution in the i-th column is given
   // by the sum of squares of elements n+1:m in that column.
   //
   // Since we don't want the user's rhs vector to be overwritten by
   // the solution, we copy the rhs values into the solution vector "x"
   // now.  x needs to be long enough to hold both the (Nx1) solution
   // vector or the (Mx1) rhs, so size it to the max of those.
   x.resize(max_MN);
   for (auto i : IntRange<int>(0, rhs.size()))
     x(i) = rhs(i);
 
   // Make the syntax below simpler by grabbing a reference to this array.
   std::vector<T> & B = x.get_values();
 
   // LDB
   // The leading dimension of the array B. LDB >= max(1,max(M,N)).
   PetscBLASInt LDB = x.size();
 
   // S is double precision array, dimension (min(M,N))
   // The singular values of A in decreasing order.
   // The condition number of A in the 2-norm = S(1)/S(min(m,n)).
   std::vector<T> S(min_MN);
 
   // RCOND
   // Used to determine the effective rank of A.  Singular values
   // S(i) <= RCOND*S(1) are treated as zero.  If RCOND < 0, machine
   // precision is used instead.
   Real RCOND = rcond;
 
   // RANK
   // The effective rank of A, i.e., the number of singular values
   // which are greater than RCOND*S(1).
   PetscBLASInt RANK = 0;
 
   // LWORK
   // The dimension of the array WORK. LWORK >= 1, and also:
   // LWORK >= 3*min(M,N) + max( 2*min(M,N), max(M,N), NRHS )
   // For good performance, LWORK should generally be larger.
   //
   // If LWORK = -1, then a workspace query is assumed; the routine
   // only calculates the optimal size of the WORK array, returns
   // this value as the first entry of the WORK array, and no error
   // message related to LWORK is issued by XERBLA.
   //
   // The factor of 3/2 is arbitrary and is used to satisfy the "should
   // generally be larger" clause.
   PetscBLASInt LWORK = (3*min_MN + std::max(2*min_MN, std::max(max_MN, NRHS))) * 3/2;
 
   // WORK is double precision array, dimension (MAX(1,LWORK))
   // On exit, if INFO = 0, WORK(1) returns the optimal LWORK.
   std::vector<T> WORK(LWORK);
 
   // INFO
   // = 0:  successful exit
   // < 0:  if INFO = -i, the i-th argument had an illegal value.
   // > 0:  the algorithm for computing the SVD failed to converge;
   //       if INFO = i, i off-diagonal elements of an intermediate
   //       bidiagonal form did not converge to zero.
   PetscBLASInt INFO = 0;
 
   // LAPACKgelss_(const PetscBLASInt *, // M
   //              const PetscBLASInt *, // N
   //              const PetscBLASInt *, // NRHS
   //              PetscScalar *,        // A
   //              const PetscBLASInt *, // LDA
   //              PetscScalar *,        // B
   //              const PetscBLASInt *, // LDB
   //              PetscReal *,          // S(out) = singular values of A in increasing order
   //              const PetscReal *,    // RCOND = tolerance for singular values
   //              PetscBLASInt *,       // RANK(out) = number of "non-zero" singular values
   //              PetscScalar *,        // WORK
   //              const PetscBLASInt *, // LWORK
   //              PetscBLASInt *);      // INFO
   LAPACKgelss_(&M, &N, &NRHS, A_trans_vals.data(), &LDA, B.data(), &LDB, S.data(), &RCOND, &RANK, WORK.data(), &LWORK, &INFO);
 
   // Check for errors in the Lapack call
   if (INFO < 0)
     libmesh_error_msg("Error, argument " << -INFO << " to LAPACKgelss_ had an illegal value.");
   if (INFO > 0)
     libmesh_error_msg("The algorithm for computing the SVD failed to converge!");
 
   // Debugging: print singular values and information about condition number:
   // libMesh::err << "RCOND=" << RCOND << std::endl;
   // libMesh::err << "Singular values: " << std::endl;
   // for (std::size_t i=0; i<S.size(); ++i)
   //   libMesh::err << S[i] << std::endl;
   // libMesh::err << "The condition number of A is approximately: " << S[0]/S.back() << std::endl;
 
   // Lapack has already written the solution into B, but it will be
   // the wrong size for non-square problems, so we need to resize it
   // correctly.  The size of the solution vector should be the number
   // of columns of the original A matrix.  Unfortunately, resizing a
   // DenseVector currently also zeros it out (unlike a std::vector) so
   // we'll resize the underlying storage directly (the size is not
   // stored independently elsewhere).
   x.get_values().resize(this->n());
 }

◆ add() [1/2]

template<typename T >

template<typename T2 , typename T3 >

boostcopy::enable_if_c< ScalarTraits< T2 >::value, void >::type libMesh::DenseMatrixBase< T >::add	(	const T2	factor,
		const DenseMatrixBase< T3 > &	mat
	)

inlineinherited

Adds factor to every element in the matrix. This should only work if T += T2 * T3 is valid C++ and if T2 is scalar. Return type is void

Definition at line 188 of file dense_matrix_base.h.

References libMesh::DenseMatrixBase< T >::el(), libMesh::DenseMatrixBase< T >::m(), and libMesh::DenseMatrixBase< T >::n().

 {
   libmesh_assert_equal_to (this->m(), mat.m());
   libmesh_assert_equal_to (this->n(), mat.n());
 
   for (unsigned int j=0; j<this->n(); j++)
     for (unsigned int i=0; i<this->m(); i++)
       this->el(i,j) += factor*mat.el(i,j);
 }

◆ add() [2/2]

template<typename T >

template<typename T2 , typename T3 >

boostcopy::enable_if_c< ScalarTraits< T2 >::value, void >::type libMesh::DenseMatrix< T >::add	(	const T2	factor,
		const DenseMatrix< T3 > &	mat
	)

inline

Adds factor times mat to this matrix.

Returns: A reference to *this.

Definition at line 884 of file dense_matrix.h.

Referenced by libMesh::FEMSystem::assembly().

 {
   libmesh_assert_equal_to (this->m(), mat.m());
   libmesh_assert_equal_to (this->n(), mat.n());
 
   for (unsigned int i=0; i<this->m(); i++)
     for (unsigned int j=0; j<this->n(); j++)
       (*this)(i,j) += factor * mat(i,j);
 }

◆ cholesky_solve()

template<typename T >

template<typename T2 >

void libMesh::DenseMatrix< T >::cholesky_solve	(	const DenseVector< T2 > &	b,
		DenseVector< T2 > &	x
	)

For symmetric positive definite (SPD) matrices. A Cholesky factorization of A such that A = L L^T is about twice as fast as a standard LU factorization. Therefore you can use this method if you know a-priori that the matrix is SPD. If the matrix is not SPD, an error is generated. One nice property of Cholesky decompositions is that they do not require pivoting for stability.

Note: This method may also be used when A is real-valued and x and b are complex-valued.

Definition at line 929 of file dense_matrix_impl.h.

Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::coarsened_dof_values(), libMesh::FEGenericBase< FEOutputType< T >::type >::compute_periodic_constraints(), libMesh::FEGenericBase< FEOutputType< T >::type >::compute_proj_constraints(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), libMesh::BoundaryProjectSolution::operator()(), and libMesh::HPCoarsenTest::select_refinement().

 {
   // Check for a previous decomposition
   switch(this->_decomposition_type)
     {
     case NONE:
       {
         this->_cholesky_decompose ();
         break;
       }
 
     case CHOLESKY:
       {
         // Already factored, just need to call back_substitute.
         break;
       }
 
     default:
       libmesh_error_msg("Error! This matrix already has a different decomposition...");
     }
 
   // Perform back substitution
   this->_cholesky_back_substitute (b, x);
 }

◆ condense() [1/2]

template<typename T >

void libMesh::DenseMatrixBase< T >::condense	(	const unsigned int	i,
		const unsigned int	j,
		const T	val,
		DenseVectorBase< T > &	rhs
	)

protectedinherited

Condense-out the (i,j) entry of the matrix, forcing it to take on the value val. This is useful in numerical simulations for applying boundary conditions. Preserves the symmetry of the matrix.

Definition at line 58 of file dense_matrix_base.C.

References libMesh::DenseVectorBase< T >::el(), and libMesh::DenseVectorBase< T >::size().

Referenced by libMesh::DenseMatrix< Number >::condense().

 {
   libmesh_assert_equal_to (this->_m, rhs.size());
   libmesh_assert_equal_to (iv, jv);
 
 
   // move the known value into the RHS
   // and zero the column
   for (unsigned int i=0; i<this->m(); i++)
     {
       rhs.el(i) -= this->el(i,jv)*val;
       this->el(i,jv) = 0.;
     }
 
   // zero the row
   for (unsigned int j=0; j<this->n(); j++)
     this->el(iv,j) = 0.;
 
   this->el(iv,jv) = 1.;
   rhs.el(iv) = val;
 
 }

◆ condense() [2/2]

template<typename T>

void libMesh::DenseMatrix< T >::condense	(	const unsigned int	i,
		const unsigned int	j,
		const T	val,
		DenseVector< T > &	rhs
	)

inline

Condense-out the (i,j) entry of the matrix, forcing it to take on the value val. This is useful in numerical simulations for applying boundary conditions. Preserves the symmetry of the matrix.

Definition at line 354 of file dense_matrix.h.

358 { DenseMatrixBase<T>::condense (i, j, val, rhs); }

libMesh::DenseMatrixBase::condense

void condense(const unsigned int i, const unsigned int j, const T val, DenseVectorBase< T > &rhs)

Definition: dense_matrix_base.C:58

◆ det()

template<typename T >

T libMesh::DenseMatrix< T >::det ( )

Returns: The determinant of the matrix.

Note: Implemented by computing an LU decomposition and then taking the product of the diagonal terms. Therefore this is a non-const method which modifies the entries of the matrix.

Definition at line 868 of file dense_matrix_impl.h.

 {
   switch(this->_decomposition_type)
     {
     case NONE:
       {
         // First LU decompose the matrix.
         // Note that the lu_decompose routine will check to see if the
         // matrix is square so we don't worry about it.
         if (this->use_blas_lapack)
           this->_lu_decompose_lapack();
         else
           this->_lu_decompose ();
       }
     case LU:
     case LU_BLAS_LAPACK:
       {
         // Already decomposed, don't do anything
         break;
       }
     default:
       libmesh_error_msg("Error! Can't compute the determinant under the current decomposition.");
     }
 
   // A variable to keep track of the running product of diagonal terms.
   T determinant = 1.;
 
   // Loop over diagonal terms, computing the product.  In practice,
   // be careful because this value could easily become too large to
   // fit in a double or float.  To be safe, one should keep track of
   // the power (of 10) of the determinant in a separate variable
   // and maintain an order 1 value for the determinant itself.
   unsigned int n_interchanges = 0;
   for (unsigned int i=0; i<this->m(); i++)
     {
       if (this->_decomposition_type==LU)
         if (_pivots[i] != static_cast<pivot_index_t>(i))
           n_interchanges++;
 
       // Lapack pivots are 1-based!
       if (this->_decomposition_type==LU_BLAS_LAPACK)
         if (_pivots[i] != static_cast<pivot_index_t>(i+1))
           n_interchanges++;
 
       determinant *= (*this)(i,i);
     }
 
   // Compute sign of determinant, depends on number of row interchanges!
   // The sign should be (-1)^{n}, where n is the number of interchanges.
   Real sign = n_interchanges % 2 == 0 ? 1. : -1.;
 
   return sign*determinant;
 }

◆ el() [1/2]

template<typename T>

virtual T libMesh::DenseMatrix< T >::el	(	const unsigned int	i,
		const unsigned int	j
	)		const

inlineoverridevirtual

Returns: The (i,j) element of the matrix. Since internal data representations may differ, you must redefine this function.

Implements libMesh::DenseMatrixBase< T >.

Definition at line 88 of file dense_matrix.h.

90 { return (*this)(i,j); }

◆ el() [2/2]

template<typename T>

virtual T& libMesh::DenseMatrix< T >::el	(	const unsigned int	i,
		const unsigned int	j
	)

inlineoverridevirtual

Returns: The (i,j) element of the matrix as a writable reference. Since internal data representations may differ, you must redefine this function.

Implements libMesh::DenseMatrixBase< T >.

Definition at line 92 of file dense_matrix.h.

94 { return (*this)(i,j); }

◆ evd()

template<typename T>

void libMesh::DenseMatrix< T >::evd	(	DenseVector< T > &	lambda_real,
		DenseVector< T > &	lambda_imag
	)

Compute the eigenvalues (both real and imaginary parts) of a general matrix.

Warning: the contents of *this are overwritten by this function!

The implementation requires the LAPACKgeev_ function which is wrapped by PETSc.

Definition at line 824 of file dense_matrix_impl.h.

 {
   // We use the LAPACK eigenvalue problem implementation
   _evd_lapack(lambda_real, lambda_imag);
 }

◆ evd_left()

template<typename T>

void libMesh::DenseMatrix< T >::evd_left	(	DenseVector< T > &	lambda_real,
		DenseVector< T > &	lambda_imag,
		DenseMatrix< T > &	VL
	)

Compute the eigenvalues (both real and imaginary parts) and left eigenvectors of a general matrix, 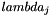$ A $ .

Warning: the contents of *this are overwritten by this function!

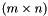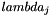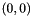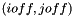The left eigenvector $ u_j $ of $ A $ satisfies: $ u_j^H A = lambda_j u_j^H $ where $ u_j^H $ denotes the conjugate-transpose of $ u_j $ .

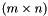If the j-th and (j+1)-st eigenvalues form a complex conjugate pair, then the j-th and (j+1)-st columns of VL "share" their real-valued storage in the following way: u_j = VL(:,j) + i*VL(:,j+1) and u_{j+1} = VL(:,j) - i*VL(:,j+1).

The implementation requires the LAPACKgeev_ routine which is provided by PETSc.

Definition at line 834 of file dense_matrix_impl.h.

 {
   // We use the LAPACK eigenvalue problem implementation
   _evd_lapack(lambda_real, lambda_imag, &VL, nullptr);
 }

◆ evd_left_and_right()

template<typename T>

void libMesh::DenseMatrix< T >::evd_left_and_right	(	DenseVector< T > &	lambda_real,
		DenseVector< T > &	lambda_imag,
		DenseMatrix< T > &	VL,
		DenseMatrix< T > &	VR
	)

Compute the eigenvalues (both real and imaginary parts) as well as the left and right eigenvectors of a general matrix.

Warning: the contents of *this are overwritten by this function!

See the documentation of the evd_left() and evd_right() functions for more information. The implementation requires the LAPACKgeev_ routine which is provided by PETSc.

Definition at line 856 of file dense_matrix_impl.h.

 {
   // We use the LAPACK eigenvalue problem implementation
   _evd_lapack(lambda_real, lambda_imag, &VL, &VR);
 }

◆ evd_right()

template<typename T>

void libMesh::DenseMatrix< T >::evd_right	(	DenseVector< T > &	lambda_real,
		DenseVector< T > &	lambda_imag,
		DenseMatrix< T > &	VR
	)

Compute the eigenvalues (both real and imaginary parts) and right eigenvectors of a general matrix, 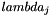$ A $ .

Warning: the contents of *this are overwritten by this function!

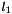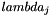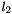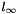The right eigenvector $ v_j $ of $ A $ satisfies: $ A v_j = lambda_j v_j $ where $ lambda_j $ is its corresponding eigenvalue.

Note: If the j-th and (j+1)-st eigenvalues form a complex conjugate pair, then the j-th and (j+1)-st columns of VR "share" their real-valued storage in the following way: v_j = VR(:,j) + i*VR(:,j+1) and v_{j+1} = VR(:,j) - i*VR(:,j+1).

The implementation requires the LAPACKgeev_ routine which is provided by PETSc.

Definition at line 845 of file dense_matrix_impl.h.

 {
   // We use the LAPACK eigenvalue problem implementation
   _evd_lapack(lambda_real, lambda_imag, nullptr, &VR);
 }

◆ get_principal_submatrix() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::get_principal_submatrix	(	unsigned int	sub_m,
		unsigned int	sub_n,
		DenseMatrix< T > &	dest
	)		const

Put the sub_m x sub_n principal submatrix into dest.

Definition at line 556 of file dense_matrix_impl.h.

 {
   libmesh_assert( (sub_m <= this->m()) && (sub_n <= this->n()) );
 
   dest.resize(sub_m, sub_n);
   for (unsigned int i=0; i<sub_m; i++)
     for (unsigned int j=0; j<sub_n; j++)
       dest(i,j) = (*this)(i,j);
 }

◆ get_principal_submatrix() [2/2]

template<typename T>

void libMesh::DenseMatrix< T >::get_principal_submatrix	(	unsigned int	sub_m,
		DenseMatrix< T > &	dest
	)		const

Put the sub_m x sub_m principal submatrix into dest.

Definition at line 586 of file dense_matrix_impl.h.

 {
   get_principal_submatrix(sub_m, sub_m, dest);
 }

◆ get_transpose()

template<typename T>

void libMesh::DenseMatrix< T >::get_transpose ( DenseMatrix< T > & dest ) const

Put the tranposed matrix into dest.

Definition at line 594 of file dense_matrix_impl.h.

 {
   dest.resize(this->n(), this->m());
 
   for (unsigned int i=0; i<dest.m(); i++)
     for (unsigned int j=0; j<dest.n(); j++)
       dest(i,j) = (*this)(j,i);
 }

◆ get_values() [1/2]

template<typename T>

std::vector<T>& libMesh::DenseMatrix< T >::get_values ( )

inline

Returns: A reference to the underlying data storage vector.

This should be used with caution (i.e. one should not change the size of the vector, etc.) but is useful for interoperating with low level BLAS routines which expect a simple array.

Definition at line 341 of file dense_matrix.h.

Referenced by libMesh::DenseMatrix< Number >::_evd_lapack(), libMesh::DenseMatrix< Number >::_matvec_blas(), libMesh::DenseMatrix< Number >::_multiply_blas(), libMesh::DenseMatrix< Number >::_svd_lapack(), libMesh::DenseMatrix< Number >::_svd_solve_lapack(), libMesh::PetscMatrix< T >::add_block_matrix(), libMesh::EpetraMatrix< T >::add_matrix(), and libMesh::PetscMatrix< T >::add_matrix().

341 { return _val; }

libMesh::DenseMatrix::_val

std::vector< T > _val

Definition: dense_matrix.h:532

◆ get_values() [2/2]

template<typename T>

const std::vector<T>& libMesh::DenseMatrix< T >::get_values ( ) const

inline

Returns: A constant reference to the underlying data storage vector.

Definition at line 346 of file dense_matrix.h.

346 { return _val; }

libMesh::DenseMatrix::_val

std::vector< T > _val

Definition: dense_matrix.h:532

◆ l1_norm()

template<typename T >

Real libMesh::DenseMatrix< T >::l1_norm ( ) const

inline

Returns: The l1-norm of the matrix, that is, the max column sum:

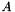$|M|_1 = max_{all columns j} \sum_{all rows i} |M_ij|$ ,

This is the natural matrix norm that is compatible to the l1-norm for vectors, i.e. 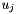$|Mv|_1 \leq |M|_1 |v|_1$ .

Definition at line 991 of file dense_matrix.h.

Referenced by libMesh::FEMSystem::assembly().

 {
   libmesh_assert (this->_m);
   libmesh_assert (this->_n);
 
   Real columnsum = 0.;
   for (unsigned int i=0; i!=this->_m; i++)
     {
       columnsum += std::abs((*this)(i,0));
     }
   Real my_max = columnsum;
   for (unsigned int j=1; j!=this->_n; j++)
     {
       columnsum = 0.;
       for (unsigned int i=0; i!=this->_m; i++)
         {
           columnsum += std::abs((*this)(i,j));
         }
       my_max = (my_max > columnsum? my_max : columnsum);
     }
   return my_max;
 }

◆ left_multiply() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::left_multiply ( const DenseMatrixBase< T > & M2 )

overridevirtual

Performs the operation: (*this) <- M2 * (*this)

Implements libMesh::DenseMatrixBase< T >.

Definition at line 40 of file dense_matrix_impl.h.

 {
   if (this->use_blas_lapack)
     this->_multiply_blas(M2, LEFT_MULTIPLY);
   else
     {
       // (*this) <- M2 * (*this)
       // Where:
       // (*this) = (m x n),
       // M2      = (m x p),
       // M3      = (p x n)
 
       // M3 is a copy of *this before it gets resize()d
       DenseMatrix<T> M3(*this);
 
       // Resize *this so that the result can fit
       this->resize (M2.m(), M3.n());
 
       // Call the multiply function in the base class
       this->multiply(*this, M2, M3);
     }
 }

◆ left_multiply() [2/2]

template<typename T >

template<typename T2 >

void libMesh::DenseMatrix< T >::left_multiply ( const DenseMatrixBase< T2 > & M2 )

Left multiplies by the matrix M2 of different type

Definition at line 67 of file dense_matrix_impl.h.

 {
   // (*this) <- M2 * (*this)
   // Where:
   // (*this) = (m x n),
   // M2      = (m x p),
   // M3      = (p x n)
 
   // M3 is a copy of *this before it gets resize()d
   DenseMatrix<T> M3(*this);
 
   // Resize *this so that the result can fit
   this->resize (M2.m(), M3.n());
 
   // Call the multiply function in the base class
   this->multiply(*this, M2, M3);
 }

◆ left_multiply_transpose() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::left_multiply_transpose ( const DenseMatrix< T > & A )

Left multiplies by the transpose of the matrix A.

Definition at line 88 of file dense_matrix_impl.h.

Referenced by libMesh::DofMap::constrain_element_matrix(), libMesh::DofMap::constrain_element_matrix_and_vector(), and libMesh::DofMap::heterogenously_constrain_element_matrix_and_vector().

 {
   if (this->use_blas_lapack)
     this->_multiply_blas(A, LEFT_MULTIPLY_TRANSPOSE);
   else
     {
       //Check to see if we are doing (A^T)*A
       if (this == &A)
         {
           //libmesh_here();
           DenseMatrix<T> B(*this);
 
           // Simple but inefficient way
           // return this->left_multiply_transpose(B);
 
           // More efficient, but more code way
           // If A is mxn, the result will be a square matrix of Size n x n.
           const unsigned int n_rows = A.m();
           const unsigned int n_cols = A.n();
 
           // resize() *this and also zero out all entries.
           this->resize(n_cols,n_cols);
 
           // Compute the lower-triangular part
           for (unsigned int i=0; i<n_cols; ++i)
             for (unsigned int j=0; j<=i; ++j)
               for (unsigned int k=0; k<n_rows; ++k) // inner products are over n_rows
                 (*this)(i,j) += B(k,i)*B(k,j);
 
           // Copy lower-triangular part into upper-triangular part
           for (unsigned int i=0; i<n_cols; ++i)
             for (unsigned int j=i+1; j<n_cols; ++j)
               (*this)(i,j) = (*this)(j,i);
         }
 
       else
         {
           DenseMatrix<T> B(*this);
 
           this->resize (A.n(), B.n());
 
           libmesh_assert_equal_to (A.m(), B.m());
           libmesh_assert_equal_to (this->m(), A.n());
           libmesh_assert_equal_to (this->n(), B.n());
 
           const unsigned int m_s = A.n();
           const unsigned int p_s = A.m();
           const unsigned int n_s = this->n();
 
           // Do it this way because there is a
           // decent chance (at least for constraint matrices)
           // that A.transpose(i,k) = 0.
           for (unsigned int i=0; i<m_s; i++)
             for (unsigned int k=0; k<p_s; k++)
               if (A.transpose(i,k) != 0.)
                 for (unsigned int j=0; j<n_s; j++)
                   (*this)(i,j) += A.transpose(i,k)*B(k,j);
         }
     }
 
 }

◆ left_multiply_transpose() [2/2]

template<typename T >

template<typename T2 >

void libMesh::DenseMatrix< T >::left_multiply_transpose ( const DenseMatrix< T2 > & A )

Left multiplies by the transpose of the matrix A which contains a different numerical type.

Definition at line 154 of file dense_matrix_impl.h.

 {
   //Check to see if we are doing (A^T)*A
   if (this == &A)
     {
       //libmesh_here();
       DenseMatrix<T> B(*this);
 
       // Simple but inefficient way
       // return this->left_multiply_transpose(B);
 
       // More efficient, but more code way
       // If A is mxn, the result will be a square matrix of Size n x n.
       const unsigned int n_rows = A.m();
       const unsigned int n_cols = A.n();
 
       // resize() *this and also zero out all entries.
       this->resize(n_cols,n_cols);
 
       // Compute the lower-triangular part
       for (unsigned int i=0; i<n_cols; ++i)
         for (unsigned int j=0; j<=i; ++j)
           for (unsigned int k=0; k<n_rows; ++k) // inner products are over n_rows
             (*this)(i,j) += B(k,i)*B(k,j);
 
       // Copy lower-triangular part into upper-triangular part
       for (unsigned int i=0; i<n_cols; ++i)
         for (unsigned int j=i+1; j<n_cols; ++j)
           (*this)(i,j) = (*this)(j,i);
     }
 
   else
     {
       DenseMatrix<T> B(*this);
 
       this->resize (A.n(), B.n());
 
       libmesh_assert_equal_to (A.m(), B.m());
       libmesh_assert_equal_to (this->m(), A.n());
       libmesh_assert_equal_to (this->n(), B.n());
 
       const unsigned int m_s = A.n();
       const unsigned int p_s = A.m();
       const unsigned int n_s = this->n();
 
       // Do it this way because there is a
       // decent chance (at least for constraint matrices)
       // that A.transpose(i,k) = 0.
       for (unsigned int i=0; i<m_s; i++)
         for (unsigned int k=0; k<p_s; k++)
           if (A.transpose(i,k) != 0.)
             for (unsigned int j=0; j<n_s; j++)
               (*this)(i,j) += A.transpose(i,k)*B(k,j);
     }
 }

◆ linfty_norm()

template<typename T >

Real libMesh::DenseMatrix< T >::linfty_norm ( ) const

inline

Returns: The linfty-norm of the matrix, that is, the max row sum:

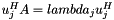$|M|_\infty = max_{all rows i} \sum_{all columns j} |M_ij|$ ,

This is the natural matrix norm that is compatible to the linfty-norm of vectors, i.e. 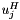$|Mv|_\infty \leq |M|_\infty |v|_\infty$ .

Definition at line 1018 of file dense_matrix.h.

 {
   libmesh_assert (this->_m);
   libmesh_assert (this->_n);
 
   Real rowsum = 0.;
   for (unsigned int j=0; j!=this->_n; j++)
     {
       rowsum += std::abs((*this)(0,j));
     }
   Real my_max = rowsum;
   for (unsigned int i=1; i!=this->_m; i++)
     {
       rowsum = 0.;
       for (unsigned int j=0; j!=this->_n; j++)
         {
           rowsum += std::abs((*this)(i,j));
         }
       my_max = (my_max > rowsum? my_max : rowsum);
     }
   return my_max;
 }

◆ lu_solve()

template<typename T>

void libMesh::DenseMatrix< T >::lu_solve	(	const DenseVector< T > &	b,
		DenseVector< T > &	x
	)

Solve the system Ax=b given the input vector b. Partial pivoting is performed by default in order to keep the algorithm stable to the effects of round-off error.

Definition at line 607 of file dense_matrix_impl.h.

Referenced by libMesh::WeightedPatchRecoveryErrorEstimator::EstimateError::operator()(), and libMesh::PatchRecoveryErrorEstimator::EstimateError::operator()().

 {
   // Check to be sure that the matrix is square before attempting
   // an LU-solve.  In general, one can compute the LU factorization of
   // a non-square matrix, but:
   //
   // Overdetermined systems (m>n) have a solution only if enough of
   // the equations are linearly-dependent.
   //
   // Underdetermined systems (m<n) typically have infinitely many
   // solutions.
   //
   // We don't want to deal with either of these ambiguous cases here...
   libmesh_assert_equal_to (this->m(), this->n());
 
   switch(this->_decomposition_type)
     {
     case NONE:
       {
         if (this->use_blas_lapack)
           this->_lu_decompose_lapack();
         else
           this->_lu_decompose ();
         break;
       }
 
     case LU_BLAS_LAPACK:
       {
         // Already factored, just need to call back_substitute.
         if (this->use_blas_lapack)
           break;
       }
       libmesh_fallthrough();
 
     case LU:
       {
         // Already factored, just need to call back_substitute.
         if (!(this->use_blas_lapack))
           break;
       }
       libmesh_fallthrough();
 
     default:
       libmesh_error_msg("Error! This matrix already has a different decomposition...");
     }
 
   if (this->use_blas_lapack)
     this->_lu_back_substitute_lapack (b, x);
   else
     this->_lu_back_substitute (b, x);
 }

◆ m()

template<typename T>

unsigned int libMesh::DenseMatrixBase< T >::m ( ) const

inlineinherited

Returns: The row-dimension of the matrix.

Definition at line 102 of file dense_matrix_base.h.

References libMesh::DenseMatrixBase< T >::_m.

102 { return _m; }

libMesh::DenseMatrixBase::_m

unsigned int _m

Definition: dense_matrix_base.h:169

◆ max()

template<typename T >

Real libMesh::DenseMatrix< T >::max ( ) const

inline

Returns: The maximum entry in the matrix, or the maximum real part in the case of complex numbers.

Definition at line 970 of file dense_matrix.h.

 {
   libmesh_assert (this->_m);
   libmesh_assert (this->_n);
   Real my_max = libmesh_real((*this)(0,0));
 
   for (unsigned int i=0; i!=this->_m; i++)
     {
       for (unsigned int j=0; j!=this->_n; j++)
         {
           Real current = libmesh_real((*this)(i,j));
           my_max = (my_max > current? my_max : current);
         }
     }
   return my_max;
 }

◆ min()

template<typename T >

Real libMesh::DenseMatrix< T >::min ( ) const

inline

Returns: The minimum entry in the matrix, or the minimum real part in the case of complex numbers.

Definition at line 949 of file dense_matrix.h.

 {
   libmesh_assert (this->_m);
   libmesh_assert (this->_n);
   Real my_min = libmesh_real((*this)(0,0));
 
   for (unsigned int i=0; i!=this->_m; i++)
     {
       for (unsigned int j=0; j!=this->_n; j++)
         {
           Real current = libmesh_real((*this)(i,j));
           my_min = (my_min < current? my_min : current);
         }
     }
   return my_min;
 }

◆ multiply()

template<typename T >

void libMesh::DenseMatrixBase< T >::multiply	(	DenseMatrixBase< T > &	M1,
		const DenseMatrixBase< T > &	M2,
		const DenseMatrixBase< T > &	M3
	)

staticprotectedinherited

Helper function - Performs the computation M1 = M2 * M3 where: M1 = (m x n) M2 = (m x p) M3 = (p x n)

Definition at line 31 of file dense_matrix_base.C.

References libMesh::DenseMatrixBase< T >::el(), libMesh::DenseMatrixBase< T >::m(), and libMesh::DenseMatrixBase< T >::n().

 {
   // Assertions to make sure we have been
   // passed matrices of the correct dimension.
   libmesh_assert_equal_to (M1.m(), M2.m());
   libmesh_assert_equal_to (M1.n(), M3.n());
   libmesh_assert_equal_to (M2.n(), M3.m());
 
   const unsigned int m_s = M2.m();
   const unsigned int p_s = M2.n();
   const unsigned int n_s = M1.n();
 
   // Do it this way because there is a
   // decent chance (at least for constraint matrices)
   // that M3(k,j) = 0. when right-multiplying.
   for (unsigned int k=0; k<p_s; k++)
     for (unsigned int j=0; j<n_s; j++)
       if (M3.el(k,j) != 0.)
         for (unsigned int i=0; i<m_s; i++)
           M1.el(i,j) += M2.el(i,k) * M3.el(k,j);
 }

◆ n()

template<typename T>

unsigned int libMesh::DenseMatrixBase< T >::n ( ) const

inlineinherited

Returns: The column-dimension of the matrix.

Definition at line 107 of file dense_matrix_base.h.

References libMesh::DenseMatrixBase< T >::_n.

107 { return _n; }

libMesh::DenseMatrixBase::_n

unsigned int _n

Definition: dense_matrix_base.h:174

◆ operator!=()

template<typename T>

bool libMesh::DenseMatrix< T >::operator!= ( const DenseMatrix< T > & mat ) const

inline

Returns: true if mat is not exactly equal to this matrix, false otherwise.

Definition at line 912 of file dense_matrix.h.

 {
   for (std::size_t i=0; i<_val.size(); i++)
     if (_val[i] != mat._val[i])
       return true;
 
   return false;
 }

◆ operator()() [1/2]

template<typename T >

T libMesh::DenseMatrix< T >::operator()	(	const unsigned int	i,
		const unsigned int	j
	)		const

inline

Returns: The (i,j) element of the matrix.

Definition at line 819 of file dense_matrix.h.

 {
   libmesh_assert_less (i*j, _val.size());
   libmesh_assert_less (i, this->_m);
   libmesh_assert_less (j, this->_n);
 
 
   //  return _val[(i) + (this->_m)*(j)]; // col-major
   return _val[(i)*(this->_n) + (j)]; // row-major
 }

◆ operator()() [2/2]

template<typename T >

T & libMesh::DenseMatrix< T >::operator()	(	const unsigned int	i,
		const unsigned int	j
	)

inline

Returns: The (i,j) element of the matrix as a writable reference.

Definition at line 835 of file dense_matrix.h.

 {
   libmesh_assert_less (i*j, _val.size());
   libmesh_assert_less (i, this->_m);
   libmesh_assert_less (j, this->_n);
 
   //return _val[(i) + (this->_m)*(j)]; // col-major
   return _val[(i)*(this->_n) + (j)]; // row-major
 }

◆ operator*=()

template<typename T>

DenseMatrix< T > & libMesh::DenseMatrix< T >::operator*= ( const T factor )

inline

Multiplies every element in the matrix by factor.

Returns: A reference to *this.

Definition at line 871 of file dense_matrix.h.

 {
   this->scale(factor);
   return *this;
 }

◆ operator+=()

template<typename T>

DenseMatrix< T > & libMesh::DenseMatrix< T >::operator+= ( const DenseMatrix< T > & mat )

inline

Adds mat to this matrix.

Returns: A reference to *this.

Definition at line 925 of file dense_matrix.h.

 {
   for (std::size_t i=0; i<_val.size(); i++)
     _val[i] += mat._val[i];
 
   return *this;
 }

◆ operator-=()

template<typename T>

DenseMatrix< T > & libMesh::DenseMatrix< T >::operator-= ( const DenseMatrix< T > & mat )

inline

Subtracts mat from this matrix.

Returns: A reference to *this.

Definition at line 937 of file dense_matrix.h.

 {
   for (std::size_t i=0; i<_val.size(); i++)
     _val[i] -= mat._val[i];
 
   return *this;
 }

◆ operator=() [1/3]

template<typename T>

DenseMatrix& libMesh::DenseMatrix< T >::operator= ( const DenseMatrix< T > & )

default

◆ operator=() [2/3]

template<typename T>

DenseMatrix& libMesh::DenseMatrix< T >::operator= ( DenseMatrix< T > && )

default

◆ operator=() [3/3]

template<typename T >

template<typename T2 >

DenseMatrix< T > & libMesh::DenseMatrix< T >::operator= ( const DenseMatrix< T2 > & other_matrix )

inline

Assignment-from-other-matrix-type operator.

Copies the dense matrix of type T2 into the present matrix. This is useful for copying real matrices into complex ones for further operations.

Returns: A reference to *this.

Definition at line 777 of file dense_matrix.h.

 {
   unsigned int mat_m = mat.m(), mat_n = mat.n();
   this->resize(mat_m, mat_n);
   for (unsigned int i=0; i<mat_m; i++)
     for (unsigned int j=0; j<mat_n; j++)
       (*this)(i,j) = mat(i,j);
 
   return *this;
 }

◆ operator==()

template<typename T>

bool libMesh::DenseMatrix< T >::operator== ( const DenseMatrix< T > & mat ) const

inline

Returns: true if mat is exactly equal to this matrix, false otherwise.

Definition at line 899 of file dense_matrix.h.

 {
   for (std::size_t i=0; i<_val.size(); i++)
     if (_val[i] != mat._val[i])
       return false;
 
   return true;
 }

◆ outer_product()

template<typename T>

void libMesh::DenseMatrix< T >::outer_product	(	const DenseVector< T > &	a,
		const DenseVector< T > &	b
	)

Computes the outer (dyadic) product of two vectors and stores in (*this).

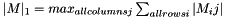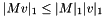The outer product of two real-valued vectors $\mathbf{a}$ and $\mathbf{b}$ is

$(\mathbf{a}\mathbf{b}^T)_{i,j} = \mathbf{a}_i \mathbf{b}_j .$

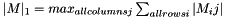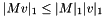The outer product of two complex-valued vectors $\mathbf{a}$ and $\mathbf{b}$ is

$(\mathbf{a}\mathbf{b}^H)_{i,j} = \mathbf{a}_i \mathbf{b}^*_j ,$

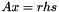where $H$ denotes the conjugate transpose of the vector and 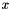$*$ denotes the complex conjugate.

Parameters

[in]	a	Vector whose entries correspond to rows in the product matrix.
[in]	b	Vector whose entries correspond to columns in the product matrix.

Definition at line 571 of file dense_matrix_impl.h.

 {
   const unsigned int m = a.size();
   const unsigned int n = b.size();
 
   this->resize(m, n);
   for (unsigned int i = 0; i < m; ++i)
     for (unsigned int j = 0; j < n; ++j)
       (*this)(i,j) = a(i) * libmesh_conj(b(j));
 }

◆ print()

template<typename T >

void libMesh::DenseMatrixBase< T >::print ( std::ostream & os = libMesh::out ) const

inherited

Pretty-print the matrix, by default to libMesh::out.

Definition at line 110 of file dense_matrix_base.C.

 {
   for (unsigned int i=0; i<this->m(); i++)
     {
       for (unsigned int j=0; j<this->n(); j++)
         os << std::setw(8)
            << this->el(i,j) << " ";
 
       os << std::endl;
     }
 
   return;
 }

◆ print_scientific()

template<typename T >

void libMesh::DenseMatrixBase< T >::print_scientific	(	std::ostream &	os,
		unsigned	precision = `8`
	)		const

inherited

Prints the matrix entries with more decimal places in scientific notation.

Definition at line 86 of file dense_matrix_base.C.

 {
   // save the initial format flags
   std::ios_base::fmtflags os_flags = os.flags();
 
   // Print the matrix entries.
   for (unsigned int i=0; i<this->m(); i++)
     {
       for (unsigned int j=0; j<this->n(); j++)
         os << std::setw(15)
            << std::scientific
            << std::setprecision(precision)
            << this->el(i,j) << " ";
 
       os << std::endl;
     }
 
   // reset the original format flags
   os.flags(os_flags);
 }

◆ resize()

template<typename T >

void libMesh::DenseMatrix< T >::resize	(	const unsigned int	new_m,
		const unsigned int	new_n
	)

inline

Resize the matrix. Will never free memory, but may allocate more. Sets all elements to 0.

Definition at line 792 of file dense_matrix.h.

Referenced by libMesh::DenseMatrix< Number >::_evd_lapack(), libMesh::DenseMatrix< Number >::_svd_lapack(), libMesh::HPCoarsenTest::add_projection(), libMesh::DofMap::build_constraint_matrix(), libMesh::DofMap::build_constraint_matrix_and_vector(), libMesh::FEGenericBase< FEOutputType< T >::type >::coarsened_dof_values(), libMesh::FEGenericBase< FEOutputType< T >::type >::compute_periodic_constraints(), libMesh::FEGenericBase< FEOutputType< T >::type >::compute_proj_constraints(), libMesh::DenseMatrix< Number >::get_principal_submatrix(), libMesh::DenseMatrix< Number >::get_transpose(), libMesh::DGFEMContext::neighbor_side_fe_reinit(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), libMesh::BoundaryProjectSolution::operator()(), libMesh::FEMContext::pre_fe_reinit(), libMesh::DenseMatrix< Number >::resize(), and libMesh::HPCoarsenTest::select_refinement().

 {
   _val.resize(new_m*new_n);
 
   this->_m = new_m;
   this->_n = new_n;
 
   // zero and set decomposition_type to NONE
   this->zero();
 }

◆ right_multiply() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::right_multiply ( const DenseMatrixBase< T > & M3 )

overridevirtual

Performs the operation: (*this) <- (*this) * M3

Implements libMesh::DenseMatrixBase< T >.

Definition at line 213 of file dense_matrix_impl.h.

Referenced by libMesh::DofMap::build_constraint_matrix(), libMesh::DofMap::build_constraint_matrix_and_vector(), libMesh::DofMap::constrain_element_matrix(), libMesh::DofMap::constrain_element_matrix_and_vector(), libMesh::DofMap::heterogenously_constrain_element_matrix_and_vector(), and libMesh::FESubdivision::init_shape_functions().

 {
   if (this->use_blas_lapack)
     this->_multiply_blas(M3, RIGHT_MULTIPLY);
   else
     {
       // (*this) <- M3 * (*this)
       // Where:
       // (*this) = (m x n),
       // M2      = (m x p),
       // M3      = (p x n)
 
       // M2 is a copy of *this before it gets resize()d
       DenseMatrix<T> M2(*this);
 
       // Resize *this so that the result can fit
       this->resize (M2.m(), M3.n());
 
       this->multiply(*this, M2, M3);
     }
 }

◆ right_multiply() [2/2]

template<typename T >

template<typename T2 >

void libMesh::DenseMatrix< T >::right_multiply ( const DenseMatrixBase< T2 > & M2 )

Right multiplies by the matrix M2 of different type

Definition at line 239 of file dense_matrix_impl.h.

 {
   // (*this) <- M3 * (*this)
   // Where:
   // (*this) = (m x n),
   // M2      = (m x p),
   // M3      = (p x n)
 
   // M2 is a copy of *this before it gets resize()d
   DenseMatrix<T> M2(*this);
 
   // Resize *this so that the result can fit
   this->resize (M2.m(), M3.n());
 
   this->multiply(*this, M2, M3);
 }

◆ right_multiply_transpose() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::right_multiply_transpose ( const DenseMatrix< T > & A )

Right multiplies by the transpose of the matrix A

Definition at line 260 of file dense_matrix_impl.h.

 {
   if (this->use_blas_lapack)
     this->_multiply_blas(B, RIGHT_MULTIPLY_TRANSPOSE);
   else
     {
       //Check to see if we are doing B*(B^T)
       if (this == &B)
         {
           //libmesh_here();
           DenseMatrix<T> A(*this);
 
           // Simple but inefficient way
           // return this->right_multiply_transpose(A);
 
           // More efficient, more code
           // If B is mxn, the result will be a square matrix of Size m x m.
           const unsigned int n_rows = B.m();
           const unsigned int n_cols = B.n();
 
           // resize() *this and also zero out all entries.
           this->resize(n_rows,n_rows);
 
           // Compute the lower-triangular part
           for (unsigned int i=0; i<n_rows; ++i)
             for (unsigned int j=0; j<=i; ++j)
               for (unsigned int k=0; k<n_cols; ++k) // inner products are over n_cols
                 (*this)(i,j) += A(i,k)*A(j,k);
 
           // Copy lower-triangular part into upper-triangular part
           for (unsigned int i=0; i<n_rows; ++i)
             for (unsigned int j=i+1; j<n_rows; ++j)
               (*this)(i,j) = (*this)(j,i);
         }
 
       else
         {
           DenseMatrix<T> A(*this);
 
           this->resize (A.m(), B.m());
 
           libmesh_assert_equal_to (A.n(), B.n());
           libmesh_assert_equal_to (this->m(), A.m());
           libmesh_assert_equal_to (this->n(), B.m());
 
           const unsigned int m_s = A.m();
           const unsigned int p_s = A.n();
           const unsigned int n_s = this->n();
 
           // Do it this way because there is a
           // decent chance (at least for constraint matrices)
           // that B.transpose(k,j) = 0.
           for (unsigned int j=0; j<n_s; j++)
             for (unsigned int k=0; k<p_s; k++)
               if (B.transpose(k,j) != 0.)
                 for (unsigned int i=0; i<m_s; i++)
                   (*this)(i,j) += A(i,k)*B.transpose(k,j);
         }
     }
 }

◆ right_multiply_transpose() [2/2]

template<typename T >

template<typename T2 >

void libMesh::DenseMatrix< T >::right_multiply_transpose ( const DenseMatrix< T2 > & A )

Right multiplies by the transpose of the matrix A which contains a different numerical type.

Definition at line 325 of file dense_matrix_impl.h.

 {
   //Check to see if we are doing B*(B^T)
   if (this == &B)
     {
       //libmesh_here();
       DenseMatrix<T> A(*this);
 
       // Simple but inefficient way
       // return this->right_multiply_transpose(A);
 
       // More efficient, more code
       // If B is mxn, the result will be a square matrix of Size m x m.
       const unsigned int n_rows = B.m();
       const unsigned int n_cols = B.n();
 
       // resize() *this and also zero out all entries.
       this->resize(n_rows,n_rows);
 
       // Compute the lower-triangular part
       for (unsigned int i=0; i<n_rows; ++i)
         for (unsigned int j=0; j<=i; ++j)
           for (unsigned int k=0; k<n_cols; ++k) // inner products are over n_cols
             (*this)(i,j) += A(i,k)*A(j,k);
 
       // Copy lower-triangular part into upper-triangular part
       for (unsigned int i=0; i<n_rows; ++i)
         for (unsigned int j=i+1; j<n_rows; ++j)
           (*this)(i,j) = (*this)(j,i);
     }
 
   else
     {
       DenseMatrix<T> A(*this);
 
       this->resize (A.m(), B.m());
 
       libmesh_assert_equal_to (A.n(), B.n());
       libmesh_assert_equal_to (this->m(), A.m());
       libmesh_assert_equal_to (this->n(), B.m());
 
       const unsigned int m_s = A.m();
       const unsigned int p_s = A.n();
       const unsigned int n_s = this->n();
 
       // Do it this way because there is a
       // decent chance (at least for constraint matrices)
       // that B.transpose(k,j) = 0.
       for (unsigned int j=0; j<n_s; j++)
         for (unsigned int k=0; k<p_s; k++)
           if (B.transpose(k,j) != 0.)
             for (unsigned int i=0; i<m_s; i++)
               (*this)(i,j) += A(i,k)*B.transpose(k,j);
     }
 }

◆ scale()

template<typename T>

void libMesh::DenseMatrix< T >::scale ( const T factor )

inline

Multiplies every element in the matrix by factor.

Definition at line 852 of file dense_matrix.h.

 {
   for (std::size_t i=0; i<_val.size(); i++)
     _val[i] *= factor;
 }

◆ scale_column()

template<typename T>

void libMesh::DenseMatrix< T >::scale_column	(	const unsigned int	col,
		const T	factor
	)

inline

Multiplies every element in the column col matrix by factor.

Definition at line 861 of file dense_matrix.h.

 {
   for (unsigned int i=0; i<this->m(); i++)
     (*this)(i, col) *= factor;
 }

◆ svd() [1/2]

template<typename T >

void libMesh::DenseMatrix< T >::svd ( DenseVector< Real > & sigma )

Compute the singular value decomposition of the matrix. On exit, sigma holds all of the singular values (in descending order).

The implementation uses PETSc's interface to BLAS/LAPACK. If this is not available, this function throws an error.

Definition at line 795 of file dense_matrix_impl.h.

 {
   // We use the LAPACK svd implementation
   _svd_lapack(sigma);
 }

◆ svd() [2/2]

template<typename T >

void libMesh::DenseMatrix< T >::svd	(	DenseVector< Real > &	sigma,
		DenseMatrix< Number > &	U,
		DenseMatrix< Number > &	VT
	)

Compute the "reduced" singular value decomposition of the matrix. On exit, sigma holds all of the singular values (in descending order), U holds the left singular vectors, and VT holds the transpose of the right singular vectors. In the reduced SVD, U has min(m,n) columns and VT has min(m,n) rows. (In the "full" SVD, U and VT would be square.)

The implementation uses PETSc's interface to BLAS/LAPACK. If this is not available, this function throws an error.

Definition at line 803 of file dense_matrix_impl.h.

 {
   // We use the LAPACK svd implementation
   _svd_lapack(sigma, U, VT);
 }

◆ svd_solve()

template<typename T>

void libMesh::DenseMatrix< T >::svd_solve	(	const DenseVector< T > &	rhs,
		DenseVector< T > &	x,
		Real	rcond = `std::numeric_limits<Real>::epsilon()`
	)		const

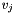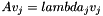Solve the system of equations $ A x = rhs $ for $ x $ in the least-squares sense. 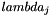$ A $ may be non-square and/or rank-deficient. You can control which singular values are treated as zero by changing the "rcond" parameter. Singular values S(i) for which S(i) <= rcond*S(1) are treated as zero for purposes of the solve. Passing a negative number for rcond forces a "machine precision" value to be used instead.

This function is marked const, since due to various implementation details, we do not need to modify the contents of A in order to compute the SVD (a copy is made internally instead).

Requires PETSc >= 3.1 since this was the first version to provide the LAPACKgelss_ wrapper.

Definition at line 814 of file dense_matrix_impl.h.

 {
   _svd_solve_lapack(rhs, x, rcond);
 }

◆ swap()

template<typename T>

void libMesh::DenseMatrix< T >::swap ( DenseMatrix< T > & other_matrix )

inline

STL-like swap method

Definition at line 762 of file dense_matrix.h.

Referenced by libMesh::EulerSolver::_general_residual(), libMesh::Euler2Solver::_general_residual(), and libMesh::NewmarkSolver::_general_residual().

 {
   std::swap(this->_m, other_matrix._m);
   std::swap(this->_n, other_matrix._n);
   _val.swap(other_matrix._val);
   DecompositionType _temp = _decomposition_type;
   _decomposition_type = other_matrix._decomposition_type;
   other_matrix._decomposition_type = _temp;
 }

◆ transpose()

template<typename T >

T libMesh::DenseMatrix< T >::transpose	(	const unsigned int	i,
		const unsigned int	j
	)		const

inline

Returns: The (i,j) element of the transposed matrix.

Definition at line 1045 of file dense_matrix.h.

Referenced by libMesh::DenseMatrix< Number >::right_multiply_transpose().

 {
   // Implement in terms of operator()
   return (*this)(j,i);
 }

◆ vector_mult() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::vector_mult	(	DenseVector< T > &	dest,
		const DenseVector< T > &	arg
	)		const

Performs the matrix-vector multiplication, dest := (*this) * arg.

Definition at line 385 of file dense_matrix_impl.h.

Referenced by libMesh::FEMap::compute_single_point_map(), libMesh::DofMap::heterogenously_constrain_element_matrix_and_vector(), and libMesh::DofMap::heterogenously_constrain_element_vector().

 {
   // Make sure the input sizes are compatible
   libmesh_assert_equal_to (this->n(), arg.size());
 
   // Resize and clear dest.
   // Note: DenseVector::resize() also zeros the vector.
   dest.resize(this->m());
 
   // Short-circuit if the matrix is empty
   if(this->m() == 0 || this->n() == 0)
     return;
 
   if (this->use_blas_lapack)
     this->_matvec_blas(1., 0., dest, arg);
   else
     {
       const unsigned int n_rows = this->m();
       const unsigned int n_cols = this->n();
 
       for (unsigned int i=0; i<n_rows; i++)
         for (unsigned int j=0; j<n_cols; j++)
           dest(i) += (*this)(i,j)*arg(j);
     }
 }

◆ vector_mult() [2/2]

template<typename T>

template<typename T2 >

void libMesh::DenseMatrix< T >::vector_mult	(	DenseVector< typename CompareTypes< T, T2 >::supertype > &	dest,
		const DenseVector< T2 > &	arg
	)		const

Performs the matrix-vector multiplication, dest := (*this) * arg on mixed types

Definition at line 416 of file dense_matrix_impl.h.

 {
   // Make sure the input sizes are compatible
   libmesh_assert_equal_to (this->n(), arg.size());
 
   // Resize and clear dest.
   // Note: DenseVector::resize() also zeros the vector.
   dest.resize(this->m());
 
   // Short-circuit if the matrix is empty
   if (this->m() == 0 || this->n() == 0)
     return;
 
   const unsigned int n_rows = this->m();
   const unsigned int n_cols = this->n();
 
   for (unsigned int i=0; i<n_rows; i++)
     for (unsigned int j=0; j<n_cols; j++)
       dest(i) += (*this)(i,j)*arg(j);
 }

◆ vector_mult_add() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::vector_mult_add	(	DenseVector< T > &	dest,
		const T	factor,
		const DenseVector< T > &	arg
	)		const

Performs the scaled matrix-vector multiplication, dest += factor * (*this) * arg.

Definition at line 511 of file dense_matrix_impl.h.

Referenced by libMesh::DofMap::build_constraint_matrix_and_vector().

 {
   // Short-circuit if the matrix is empty
   if (this->m() == 0)
     {
       dest.resize(0);
       return;
     }
 
   if (this->use_blas_lapack)
     this->_matvec_blas(factor, 1., dest, arg);
   else
     {
       DenseVector<T> temp(arg.size());
       this->vector_mult(temp, arg);
       dest.add(factor, temp);
     }
 }

◆ vector_mult_add() [2/2]

template<typename T>

template<typename T2 , typename T3 >

void libMesh::DenseMatrix< T >::vector_mult_add	(	DenseVector< typename CompareTypes< T, typename CompareTypes< T2, T3 >::supertype >::supertype > &	dest,
		const T2	factor,
		const DenseVector< T3 > &	arg
	)		const

Performs the scaled matrix-vector multiplication, dest += factor * (*this) * arg. on mixed types

Definition at line 536 of file dense_matrix_impl.h.

 {
   // Short-circuit if the matrix is empty
   if (this->m() == 0)
     {
       dest.resize(0);
       return;
     }
 
   DenseVector<typename CompareTypes<T,T3>::supertype>
     temp(arg.size());
   this->vector_mult(temp, arg);
   dest.add(factor, temp);
 }

◆ vector_mult_transpose() [1/2]

template<typename T>

void libMesh::DenseMatrix< T >::vector_mult_transpose	(	DenseVector< T > &	dest,
		const DenseVector< T > &	arg
	)		const

Performs the matrix-vector multiplication, dest := (*this)^T * arg.

Definition at line 441 of file dense_matrix_impl.h.

Referenced by libMesh::DofMap::constrain_element_dyad_matrix(), libMesh::DofMap::constrain_element_matrix_and_vector(), libMesh::DofMap::constrain_element_vector(), libMesh::DofMap::heterogenously_constrain_element_matrix_and_vector(), and libMesh::DofMap::heterogenously_constrain_element_vector().

 {
   // Make sure the input sizes are compatible
   libmesh_assert_equal_to (this->m(), arg.size());
 
   // Resize and clear dest.
   // Note: DenseVector::resize() also zeros the vector.
   dest.resize(this->n());
 
   // Short-circuit if the matrix is empty
   if (this->m() == 0)
     return;
 
   if (this->use_blas_lapack)
     {
       this->_matvec_blas(1., 0., dest, arg, /*trans=*/true);
     }
   else
     {
       const unsigned int n_rows = this->m();
       const unsigned int n_cols = this->n();
 
       // WORKS
       // for (unsigned int j=0; j<n_cols; j++)
       //   for (unsigned int i=0; i<n_rows; i++)
       //     dest(j) += (*this)(i,j)*arg(i);
 
       // ALSO WORKS, (i,j) just swapped
       for (unsigned int i=0; i<n_cols; i++)
         for (unsigned int j=0; j<n_rows; j++)
           dest(i) += (*this)(j,i)*arg(j);
     }
 }

◆ vector_mult_transpose() [2/2]

template<typename T>

template<typename T2 >

void libMesh::DenseMatrix< T >::vector_mult_transpose	(	DenseVector< typename CompareTypes< T, T2 >::supertype > &	dest,
		const DenseVector< T2 > &	arg
	)		const

Performs the matrix-vector multiplication, dest := (*this)^T * arg. on mixed types

Definition at line 480 of file dense_matrix_impl.h.

 {
   // Make sure the input sizes are compatible
   libmesh_assert_equal_to (this->m(), arg.size());
 
   // Resize and clear dest.
   // Note: DenseVector::resize() also zeros the vector.
   dest.resize(this->n());
 
   // Short-circuit if the matrix is empty
   if (this->m() == 0)
     return;
 
   const unsigned int n_rows = this->m();
   const unsigned int n_cols = this->n();
 
   // WORKS
   // for (unsigned int j=0; j<n_cols; j++)
   //   for (unsigned int i=0; i<n_rows; i++)
   //     dest(j) += (*this)(i,j)*arg(i);
 
   // ALSO WORKS, (i,j) just swapped
   for (unsigned int i=0; i<n_cols; i++)
     for (unsigned int j=0; j<n_rows; j++)
       dest(i) += (*this)(j,i)*arg(j);
 }

◆ zero()

template<typename T >

void libMesh::DenseMatrix< T >::zero ( )

inlineoverridevirtual

Set every element in the matrix to 0. You must redefine what you mean by zeroing the matrix since it depends on how your values are stored.

Implements libMesh::DenseMatrixBase< T >.

Definition at line 808 of file dense_matrix.h.

Referenced by libMesh::HPCoarsenTest::add_projection(), libMesh::FEMSystem::assembly(), libMesh::FEGenericBase< FEOutputType< T >::type >::coarsened_dof_values(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), libMesh::BoundaryProjectSolution::operator()(), and libMesh::HPCoarsenTest::select_refinement().

 {
   _decomposition_type = NONE;
 
   std::fill (_val.begin(), _val.end(), static_cast<T>(0));
 }

Member Data Documentation

◆ _decomposition_type

template<typename T>

DecompositionType libMesh::DenseMatrix< T >::_decomposition_type

private

This flag keeps track of which type of decomposition has been performed on the matrix.

Definition at line 582 of file dense_matrix.h.

Referenced by libMesh::DenseMatrix< Number >::swap().

◆ _m

template<typename T>

unsigned int libMesh::DenseMatrixBase< T >::_m

protectedinherited

The row dimension.

Definition at line 169 of file dense_matrix_base.h.

Referenced by libMesh::DenseMatrixBase< T >::m(), and libMesh::DenseMatrix< Number >::swap().

◆ _n

template<typename T>

unsigned int libMesh::DenseMatrixBase< T >::_n

protectedinherited

The column dimension.

Definition at line 174 of file dense_matrix_base.h.

Referenced by libMesh::DenseMatrixBase< T >::n(), and libMesh::DenseMatrix< Number >::swap().

◆ _pivots

template<typename T>

std::vector<pivot_index_t> libMesh::DenseMatrix< T >::_pivots

private

Definition at line 672 of file dense_matrix.h.

◆ _val

template<typename T>

std::vector<T> libMesh::DenseMatrix< T >::_val

private

The actual data values, stored as a 1D array.

Definition at line 532 of file dense_matrix.h.

Referenced by libMesh::DenseMatrix< Number >::get_values(), libMesh::DenseMatrix< Number >::operator!=(), libMesh::DenseMatrix< Number >::operator+=(), libMesh::DenseMatrix< Number >::operator-=(), libMesh::DenseMatrix< Number >::operator==(), and libMesh::DenseMatrix< Number >::swap().

◆ use_blas_lapack

template<typename T>

bool libMesh::DenseMatrix< T >::use_blas_lapack

Computes the inverse of the dense matrix (assuming it is invertible) by first computing the LU decomposition and then performing multiple back substitution steps. Follows the algorithm from Numerical Recipes in C that is available on the web.

This routine is commented out since it is not really a memory- or computationally- efficient implementation. Also, you typically don't need the actual inverse for anything, and can use something like lu_solve() instead. Run-time selectable option to turn on/off BLAS support. This was primarily used for testing purposes, and could be removed...

Definition at line 525 of file dense_matrix.h.

The documentation for this class was generated from the following files:

Public Member Functions

Public Attributes

Protected Member Functions

Static Protected Member Functions

Protected Attributes

Private Types

Private Member Functions

Private Attributes

Detailed Description

template<typename T> class libMesh::DenseMatrix< T >

Member Typedef Documentation

◆ pivot_index_t [1/2]

◆ pivot_index_t [2/2]

Member Enumeration Documentation

◆ _BLAS_Multiply_Flag

◆ DecompositionType

Constructor & Destructor Documentation

◆ DenseMatrix() [1/3]

◆ DenseMatrix() [2/3]

◆ DenseMatrix() [3/3]

◆ ~DenseMatrix()

Member Function Documentation

◆ _cholesky_back_substitute()

◆ _cholesky_decompose()

◆ _evd_lapack()

◆ _lu_back_substitute()

◆ _lu_back_substitute_lapack()

◆ _lu_decompose()

◆ _lu_decompose_lapack()

◆ _matvec_blas()

◆ _multiply_blas()

◆ _svd_helper()

◆ _svd_lapack() [1/2]

◆ _svd_lapack() [2/2]

◆ _svd_solve_lapack()

◆ add() [1/2]

◆ add() [2/2]

◆ cholesky_solve()

◆ condense() [1/2]

◆ condense() [2/2]

◆ det()

◆ el() [1/2]

◆ el() [2/2]

◆ evd()

◆ evd_left()

◆ evd_left_and_right()

◆ evd_right()

◆ get_principal_submatrix() [1/2]

◆ get_principal_submatrix() [2/2]

◆ get_transpose()

◆ get_values() [1/2]

◆ get_values() [2/2]

◆ l1_norm()

◆ left_multiply() [1/2]

◆ left_multiply() [2/2]

◆ left_multiply_transpose() [1/2]

◆ left_multiply_transpose() [2/2]

◆ linfty_norm()

◆ lu_solve()

◆ m()

◆ max()

◆ min()

◆ multiply()

◆ n()

◆ operator!=()

◆ operator()() [1/2]

◆ operator()() [2/2]

◆ operator*=()

◆ operator+=()

◆ operator-=()

◆ operator=() [1/3]

◆ operator=() [2/3]

◆ operator=() [3/3]

◆ operator==()

◆ outer_product()

◆ print()

◆ print_scientific()

◆ resize()

◆ right_multiply() [1/2]

◆ right_multiply() [2/2]

template<typename T>
class libMesh::DenseMatrix< T >