#include <fe.h>
Public Types | |
| typedef FEGenericBase< typename FEOutputType< T >::type >::OutputShape | OutputShape |
| typedef TensorTools::IncrementRank< OutputShape >::type | OutputGradient |
| typedef TensorTools::IncrementRank< OutputGradient >::type | OutputTensor |
| typedef TensorTools::DecrementRank< OutputShape >::type | OutputDivergence |
| typedef TensorTools::MakeNumber< OutputShape >::type | OutputNumber |
| typedef TensorTools::IncrementRank< OutputNumber >::type | OutputNumberGradient |
| typedef TensorTools::IncrementRank< OutputNumberGradient >::type | OutputNumberTensor |
| typedef TensorTools::DecrementRank< OutputNumber >::type | OutputNumberDivergence |
Public Member Functions | |
| FESubdivision (const FEType &fet) | |
| virtual void | reinit (const Elem *elem, const std::vector< Point > *const pts=nullptr, const std::vector< Real > *const weights=nullptr) override |
| virtual void | reinit (const Elem *, const unsigned int, const Real=TOLERANCE, const std::vector< Point > *const =nullptr, const std::vector< Real > *const =nullptr) override |
| virtual void | attach_quadrature_rule (QBase *q) override |
| virtual void | init_shape_functions (const std::vector< Point > &qp, const Elem *elem) override |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *libmesh_dbg_var(elem), const Order, const unsigned int, const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const ElemType, const Order, const unsigned int, const Point &) |
| RealGradient | shape (const Elem *, const Order, const unsigned int, const Point &) |
| RealGradient | shape (const ElemType, const Order, const unsigned int, const Point &) |
| RealGradient | shape (const Elem *, const Order, const unsigned int, const Point &) |
| RealGradient | shape (const ElemType, const Order, const unsigned int, const Point &) |
| RealGradient | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| RealGradient | shape (const ElemType, const Order, const unsigned int, const Point &) |
| RealGradient | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int, const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int, const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int, const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int, const Point &) |
| Real | shape (const ElemType type, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const Point &p) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int, const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const Elem *, const Order, const unsigned int libmesh_dbg_var(i), const Point &) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const Point &point_in) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const Point &point_in) |
| Real | shape (const ElemType, const Order, const unsigned int, const Point &) |
| Real | shape (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const Point &point_in) |
| Real | shape (const Elem *elem, const Order order, const unsigned int i, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order order, const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *libmesh_dbg_var(elem), const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order order, const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order order, const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &) |
| RealGradient | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &point_in) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &point_in) |
| Real | shape_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &point_in) |
| Real | shape_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *libmesh_dbg_var(elem), const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order order, const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order order, const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| RealGradient | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_second_deriv (const Elem *elem, const Order order, const unsigned int libmesh_dbg_var(i), const unsigned int libmesh_dbg_var(j), const Point &) |
| RealGradient | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| RealGradient | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &libmesh_dbg_var(p)) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType type, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int libmesh_dbg_var(j), const Point &point_in) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &point_in) |
| Real | shape_second_deriv (const ElemType, const Order, const unsigned int, const unsigned int, const Point &) |
| Real | shape_second_deriv (const Elem *elem, const Order libmesh_dbg_var(order), const unsigned int i, const unsigned int j, const Point &point_in) |
| Real | shape_second_deriv (const Elem *elem, const Order order, const unsigned int i, const unsigned int j, const Point &p) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *, const Order, const std::vector< Number > &, std::vector< Number > &) |
| void | nodal_soln (const Elem *, const Order, const std::vector< Number > &, std::vector< Number > &) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| void | nodal_soln (const Elem *elem, const Order order, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| virtual unsigned int | n_shape_functions () const override |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType, const Order) |
| unsigned int | n_dofs (const ElemType, const Order) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType, const Order o) |
| unsigned int | n_dofs (const ElemType, const Order o) |
| unsigned int | n_dofs (const ElemType, const Order o) |
| unsigned int | n_dofs (const ElemType, const Order o) |
| unsigned int | n_dofs (const ElemType, const Order) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs (const ElemType t, const Order o) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_at_node (const ElemType, const Order, const unsigned int) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType, const Order) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| virtual FEContinuity | get_continuity () const override |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| FEContinuity | get_continuity () const |
| virtual bool | is_hierarchic () const override |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| bool | is_hierarchic () const |
| void | dofs_on_side (const Elem *const, const Order, unsigned int, std::vector< unsigned int > &di) |
| void | dofs_on_edge (const Elem *const, const Order, unsigned int, std::vector< unsigned int > &di) |
| Point | inverse_map (const Elem *, const Point &, const Real, const bool) |
| void | inverse_map (const Elem *, const std::vector< Point > &, std::vector< Point > &, Real, bool) |
| virtual void | edge_reinit (const Elem *elem, const unsigned int edge, const Real tolerance=TOLERANCE, const std::vector< Point > *const pts=nullptr, const std::vector< Real > *const weights=nullptr) override |
| void | edge_reinit (Elem const *, unsigned int, Real, const std::vector< Point > *const, const std::vector< Real > *const) |
| virtual void | side_map (const Elem *elem, const Elem *side, const unsigned int s, const std::vector< Point > &reference_side_points, std::vector< Point > &reference_points) override |
| void | side_map (const Elem *, const Elem *, const unsigned int, const std::vector< Point > &, std::vector< Point > &) |
| virtual unsigned int | n_quadrature_points () const override |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| void | compute_constraints (DofConstraints &, DofMap &, const unsigned int, const Elem *) |
| virtual bool | shapes_need_reinit () const override |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| bool | shapes_need_reinit () const |
| std::unique_ptr< FEGenericBase< Real > > | build (const unsigned int dim, const FEType &fet) |
| std::unique_ptr< FEGenericBase< RealGradient > > | build (const unsigned int dim, const FEType &fet) |
| std::unique_ptr< FEGenericBase< Real > > | build_InfFE (const unsigned int dim, const FEType &fet) |
| std::unique_ptr< FEGenericBase< RealGradient > > | build_InfFE (const unsigned int, const FEType &) |
| const std::vector< std::vector< OutputShape > > & | get_phi () const |
| const std::vector< std::vector< OutputGradient > > & | get_dphi () const |
| const std::vector< std::vector< OutputShape > > & | get_curl_phi () const |
| const std::vector< std::vector< OutputDivergence > > & | get_div_phi () const |
| const std::vector< std::vector< OutputShape > > & | get_dphidx () const |
| const std::vector< std::vector< OutputShape > > & | get_dphidy () const |
| const std::vector< std::vector< OutputShape > > & | get_dphidz () const |
| const std::vector< std::vector< OutputShape > > & | get_dphidxi () const |
| const std::vector< std::vector< OutputShape > > & | get_dphideta () const |
| const std::vector< std::vector< OutputShape > > & | get_dphidzeta () const |
| const std::vector< std::vector< OutputTensor > > & | get_d2phi () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidx2 () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidxdy () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidxdz () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidy2 () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidydz () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidz2 () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidxi2 () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidxideta () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidxidzeta () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phideta2 () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidetadzeta () const |
| const std::vector< std::vector< OutputShape > > & | get_d2phidzeta2 () const |
| const std::vector< OutputGradient > & | get_dphase () const |
| const std::vector< Real > & | get_Sobolev_weight () const |
| const std::vector< RealGradient > & | get_Sobolev_dweight () const |
| void | print_phi (std::ostream &os) const |
| void | print_dphi (std::ostream &os) const |
| void | print_d2phi (std::ostream &os) const |
| unsigned int | get_dim () const |
| const std::vector< Point > & | get_xyz () const |
| const std::vector< Real > & | get_JxW () const |
| const std::vector< RealGradient > & | get_dxyzdxi () const |
| const std::vector< RealGradient > & | get_dxyzdeta () const |
| const std::vector< RealGradient > & | get_dxyzdzeta () const |
| const std::vector< RealGradient > & | get_d2xyzdxi2 () const |
| const std::vector< RealGradient > & | get_d2xyzdeta2 () const |
| const std::vector< RealGradient > & | get_d2xyzdzeta2 () const |
| const std::vector< RealGradient > & | get_d2xyzdxideta () const |
| const std::vector< RealGradient > & | get_d2xyzdxidzeta () const |
| const std::vector< RealGradient > & | get_d2xyzdetadzeta () const |
| const std::vector< Real > & | get_dxidx () const |
| const std::vector< Real > & | get_dxidy () const |
| const std::vector< Real > & | get_dxidz () const |
| const std::vector< Real > & | get_detadx () const |
| const std::vector< Real > & | get_detady () const |
| const std::vector< Real > & | get_detadz () const |
| const std::vector< Real > & | get_dzetadx () const |
| const std::vector< Real > & | get_dzetady () const |
| const std::vector< Real > & | get_dzetadz () const |
| const std::vector< std::vector< Point > > & | get_tangents () const |
| const std::vector< Point > & | get_normals () const |
| const std::vector< Real > & | get_curvatures () const |
| ElemType | get_type () const |
| unsigned int | get_p_level () const |
| FEType | get_fe_type () const |
| Order | get_order () const |
| void | set_fe_order (int new_order) |
| FEFamily | get_family () const |
| const FEMap & | get_fe_map () const |
| void | print_JxW (std::ostream &os) const |
| void | print_xyz (std::ostream &os) const |
| void | print_info (std::ostream &os) const |
Static Public Member Functions | |
| static Real | regular_shape (const unsigned int i, const Real v, const Real w) |
| static Real | regular_shape_deriv (const unsigned int i, const unsigned int j, const Real v, const Real w) |
| static Real | regular_shape_second_deriv (const unsigned int i, const unsigned int j, const Real v, const Real w) |
| static void | loop_subdivision_mask (std::vector< Real > &weights, const unsigned int valence) |
| static void | init_subdivision_matrix (DenseMatrix< Real > &A, unsigned int valence) |
| static OutputShape | shape (const ElemType t, const Order o, const unsigned int i, const Point &p) |
| static OutputShape | shape (const Elem *elem, const Order o, const unsigned int i, const Point &p) |
| static OutputShape | shape_deriv (const ElemType t, const Order o, const unsigned int i, const unsigned int j, const Point &p) |
| static OutputShape | shape_deriv (const Elem *elem, const Order o, const unsigned int i, const unsigned int j, const Point &p) |
| static OutputShape | shape_second_deriv (const ElemType t, const Order o, const unsigned int i, const unsigned int j, const Point &p) |
| static OutputShape | shape_second_deriv (const Elem *elem, const Order o, const unsigned int i, const unsigned int j, const Point &p) |
| static void | nodal_soln (const Elem *elem, const Order o, const std::vector< Number > &elem_soln, std::vector< Number > &nodal_soln) |
| static unsigned int | n_shape_functions (const ElemType t, const Order o) |
| static unsigned int | n_dofs (const ElemType t, const Order o) |
| static unsigned int | n_dofs_at_node (const ElemType t, const Order o, const unsigned int n) |
| static unsigned int | n_dofs_per_elem (const ElemType t, const Order o) |
| static void | dofs_on_side (const Elem *const elem, const Order o, unsigned int s, std::vector< unsigned int > &di) |
| static void | dofs_on_edge (const Elem *const elem, const Order o, unsigned int e, std::vector< unsigned int > &di) |
| static Point | inverse_map (const Elem *elem, const Point &p, const Real tolerance=TOLERANCE, const bool secure=true) |
| static void | inverse_map (const Elem *elem, const std::vector< Point > &physical_points, std::vector< Point > &reference_points, const Real tolerance=TOLERANCE, const bool secure=true) |
| static void | compute_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| static Point | map (const Elem *elem, const Point &reference_point) |
| static Point | map_xi (const Elem *elem, const Point &reference_point) |
| static Point | map_eta (const Elem *elem, const Point &reference_point) |
| static Point | map_zeta (const Elem *elem, const Point &reference_point) |
| static std::unique_ptr< FEGenericBase > | build (const unsigned int dim, const FEType &type) |
| static std::unique_ptr< FEGenericBase > | build_InfFE (const unsigned int dim, const FEType &type) |
| static void | compute_proj_constraints (DofConstraints &constraints, DofMap &dof_map, const unsigned int variable_number, const Elem *elem) |
| static void | coarsened_dof_values (const NumericVector< Number > &global_vector, const DofMap &dof_map, const Elem *coarse_elem, DenseVector< Number > &coarse_dofs, const unsigned int var, const bool use_old_dof_indices=false) |
| static void | coarsened_dof_values (const NumericVector< Number > &global_vector, const DofMap &dof_map, const Elem *coarse_elem, DenseVector< Number > &coarse_dofs, const bool use_old_dof_indices=false) |
| static void | compute_periodic_constraints (DofConstraints &constraints, DofMap &dof_map, const PeriodicBoundaries &boundaries, const MeshBase &mesh, const PointLocatorBase *point_locator, const unsigned int variable_number, const Elem *elem) |
| static bool | on_reference_element (const Point &p, const ElemType t, const Real eps=TOLERANCE) |
| static void | get_refspace_nodes (const ElemType t, std::vector< Point > &nodes) |
| static void | compute_node_constraints (NodeConstraints &constraints, const Elem *elem) |
| static void | compute_periodic_node_constraints (NodeConstraints &constraints, const PeriodicBoundaries &boundaries, const MeshBase &mesh, const PointLocatorBase *point_locator, const Elem *elem) |
| static void | print_info (std::ostream &out=libMesh::out) |
| static std::string | get_info () |
| static unsigned int | n_objects () |
| static void | enable_print_counter_info () |
| static void | disable_print_counter_info () |
Protected Types | |
| typedef std::map< std::string, std::pair< unsigned int, unsigned int > > | Counts |
Protected Member Functions | |
| virtual void | init_base_shape_functions (const std::vector< Point > &qp, const Elem *e) override |
| void | determine_calculations () |
| virtual void | compute_shape_functions (const Elem *elem, const std::vector< Point > &qp) |
| void | increment_constructor_count (const std::string &name) |
| void | increment_destructor_count (const std::string &name) |
Protected Attributes | |
| std::vector< Point > | cached_nodes |
| ElemType | last_side |
| unsigned int | last_edge |
| std::unique_ptr< FETransformationBase< FEOutputType< T >::type > > | _fe_trans |
| std::vector< std::vector< OutputShape > > | phi |
| std::vector< std::vector< OutputGradient > > | dphi |
| std::vector< std::vector< OutputShape > > | curl_phi |
| std::vector< std::vector< OutputDivergence > > | div_phi |
| std::vector< std::vector< OutputShape > > | dphidxi |
| std::vector< std::vector< OutputShape > > | dphideta |
| std::vector< std::vector< OutputShape > > | dphidzeta |
| std::vector< std::vector< OutputShape > > | dphidx |
| std::vector< std::vector< OutputShape > > | dphidy |
| std::vector< std::vector< OutputShape > > | dphidz |
| std::vector< std::vector< OutputTensor > > | d2phi |
| std::vector< std::vector< OutputShape > > | d2phidxi2 |
| std::vector< std::vector< OutputShape > > | d2phidxideta |
| std::vector< std::vector< OutputShape > > | d2phidxidzeta |
| std::vector< std::vector< OutputShape > > | d2phideta2 |
| std::vector< std::vector< OutputShape > > | d2phidetadzeta |
| std::vector< std::vector< OutputShape > > | d2phidzeta2 |
| std::vector< std::vector< OutputShape > > | d2phidx2 |
| std::vector< std::vector< OutputShape > > | d2phidxdy |
| std::vector< std::vector< OutputShape > > | d2phidxdz |
| std::vector< std::vector< OutputShape > > | d2phidy2 |
| std::vector< std::vector< OutputShape > > | d2phidydz |
| std::vector< std::vector< OutputShape > > | d2phidz2 |
| std::vector< OutputGradient > | dphase |
| std::vector< RealGradient > | dweight |
| std::vector< Real > | weight |
| std::unique_ptr< FEMap > | _fe_map |
| const unsigned int | dim |
| bool | calculations_started |
| bool | calculate_phi |
| bool | calculate_dphi |
| bool | calculate_d2phi |
| bool | calculate_curl_phi |
| bool | calculate_div_phi |
| bool | calculate_dphiref |
| FEType | fe_type |
| ElemType | elem_type |
| unsigned int | _p_level |
| QBase * | qrule |
| bool | shapes_on_quadrature |
Static Protected Attributes | |
| static Counts | _counts |
| static Threads::atomic< unsigned int > | _n_objects |
| static Threads::spin_mutex | _mutex |
| static bool | _enable_print_counter = true |
Detailed Description
Member Typedef Documentation
◆ Counts
|
protectedinherited |
Data structure to log the information. The log is identified by the class name.
Definition at line 117 of file reference_counter.h.
◆ OutputDivergence
|
inherited |
◆ OutputGradient
|
inherited |
◆ OutputNumber
|
inherited |
◆ OutputNumberDivergence
|
inherited |
◆ OutputNumberGradient
|
inherited |
◆ OutputNumberTensor
|
inherited |
◆ OutputShape
|
inherited |
◆ OutputTensor
|
inherited |
Constructor & Destructor Documentation
◆ FESubdivision()
| libMesh::FESubdivision::FESubdivision | ( | const FEType & | fet | ) |
Constructor. Creates a subdivision surface finite element. Currently only supported for two-dimensional meshes in three-dimensional space.
Definition at line 33 of file fe_subdivision_2D.C.
Member Function Documentation
◆ attach_quadrature_rule()
|
overridevirtual |
Provides the class with the quadrature rule, which provides the locations (on a reference element) where the shape functions are to be calculated.
Reimplemented from libMesh::FE< 2, SUBDIVISION >.
Definition at line 648 of file fe_subdivision_2D.C.
References libMesh::FEAbstract::elem_type, libMesh::INVALID_ELEM, and libMesh::FEAbstract::qrule.
◆ build() [1/3]
|
staticinherited |
Builds a specific finite element type. A std::unique_ptr<FEGenericBase> is returned to prevent a memory leak. This way the user need not remember to delete the object.
The build call will fail if the OutputType of this class is not compatible with the output required for the requested type
◆ build() [2/3]
|
inherited |
Definition at line 182 of file fe_base.C.
References libMesh::BERNSTEIN, libMesh::CLOUGH, libMesh::FEType::family, libMesh::HERMITE, libMesh::HIERARCHIC, libMesh::L2_HIERARCHIC, libMesh::L2_LAGRANGE, libMesh::LAGRANGE, libMesh::MONOMIAL, libMesh::SCALAR, libMesh::SUBDIVISION, libMesh::SZABAB, and libMesh::XYZ.
◆ build() [3/3]
|
inherited |
Definition at line 380 of file fe_base.C.
References libMesh::FEType::family, libMesh::LAGRANGE_VEC, and libMesh::NEDELEC_ONE.
◆ build_InfFE() [1/3]
|
staticinherited |
Builds a specific infinite element type. A std::unique_ptr<FEGenericBase> is returned to prevent a memory leak. This way the user need not remember to delete the object.
The build call will fail if the OutputShape of this class is not compatible with the output required for the requested type
◆ build_InfFE() [2/3]
|
inherited |
Definition at line 453 of file fe_base.C.
References libMesh::CARTESIAN, libMesh::FEType::inf_map, libMesh::INFINITE_MAP, libMesh::JACOBI_20_00, libMesh::JACOBI_30_00, libMesh::LAGRANGE, libMesh::LEGENDRE, and libMesh::FEType::radial_family.
◆ build_InfFE() [3/3]
|
inherited |
◆ coarsened_dof_values() [1/2]
|
staticinherited |
Creates a local projection on coarse_elem, based on the DoF values in global_vector for it's children. Computes a vector of coefficients corresponding to dof_indices for only the single given var
Definition at line 791 of file fe_base.C.
References std::abs(), libMesh::C_ONE, libMesh::Elem::child_ptr(), libMesh::Elem::child_ref_range(), libMesh::DenseMatrix< T >::cholesky_solve(), libMesh::FEType::default_quadrature_rule(), libMesh::Elem::dim(), libMesh::DISCONTINUOUS, libMesh::DofMap::dof_indices(), libMesh::FEInterface::dofs_on_edge(), libMesh::FEInterface::dofs_on_side(), libMesh::Elem::edge_index_range(), libMesh::TensorTools::inner_product(), libMesh::FEInterface::inverse_map(), libMesh::Elem::is_child_on_edge(), libMesh::Elem::is_child_on_side(), libMesh::Elem::is_vertex(), libMesh::Elem::max_descendant_p_level(), libMesh::Elem::n_children(), libMesh::FEInterface::n_dofs(), libMesh::FEInterface::n_dofs_at_node(), n_nodes, libMesh::Elem::n_nodes(), libMesh::DofMap::old_dof_indices(), libMesh::FEType::order, libMesh::Elem::p_level(), libMesh::DenseVector< T >::resize(), libMesh::DenseMatrix< T >::resize(), libMesh::Elem::side_index_range(), libMesh::TOLERANCE, libMesh::Elem::type(), libMesh::DofMap::variable_type(), libMesh::DenseMatrix< T >::zero(), libMesh::DenseVector< T >::zero(), and libMesh::zero.
◆ coarsened_dof_values() [2/2]
|
staticinherited |
Creates a local projection on coarse_elem, based on the DoF values in global_vector for it's children. Computes a vector of coefficients corresponding to all dof_indices.
Definition at line 1343 of file fe_base.C.
References libMesh::DenseVector< T >::append(), libMesh::DofMap::n_variables(), and libMesh::DenseVector< T >::resize().
◆ compute_constraints() [1/29]
|
inherited |
Definition at line 122 of file fe_scalar.C.
◆ compute_constraints() [2/29]
|
inherited |
Definition at line 129 of file fe_scalar.C.
◆ compute_constraints() [3/29]
|
inherited |
Definition at line 207 of file fe_l2_hierarchic.C.
◆ compute_constraints() [4/29]
|
inherited |
Definition at line 214 of file fe_l2_hierarchic.C.
◆ compute_constraints() [5/29]
|
inherited |
Definition at line 304 of file fe_clough.C.
◆ compute_constraints() [6/29]
|
inherited |
Definition at line 311 of file fe_clough.C.
◆ compute_constraints() [7/29]
|
inherited |
Definition at line 355 of file fe_hermite.C.
◆ compute_constraints() [8/29]
|
inherited |
Definition at line 362 of file fe_hermite.C.
◆ compute_constraints() [9/29]
|
inherited |
Definition at line 383 of file fe_hierarchic.C.
◆ compute_constraints() [10/29]
|
inherited |
Definition at line 390 of file fe_hierarchic.C.
◆ compute_constraints() [11/29]
|
staticinherited |
Computes the constraint matrix contributions (for non-conforming adapted meshes) corresponding to variable number var_number, using element-specific optimizations if possible.
◆ compute_constraints() [12/29]
|
inherited |
Definition at line 419 of file fe_monomial.C.
◆ compute_constraints() [13/29]
|
inherited |
Definition at line 420 of file fe_monomial.C.
◆ compute_constraints() [14/29]
|
inherited |
Definition at line 450 of file fe_bernstein.C.
◆ compute_constraints() [15/29]
|
inherited |
Definition at line 457 of file fe_bernstein.C.
◆ compute_constraints() [16/29]
|
inherited |
Definition at line 495 of file fe_l2_lagrange.C.
◆ compute_constraints() [17/29]
|
inherited |
Definition at line 502 of file fe_l2_lagrange.C.
◆ compute_constraints() [18/29]
|
inherited |
Definition at line 563 of file fe_nedelec_one.C.
◆ compute_constraints() [19/29]
|
inherited |
Definition at line 570 of file fe_nedelec_one.C.
◆ compute_constraints() [20/29]
|
inherited |
Definition at line 577 of file fe_nedelec_one.C.
◆ compute_constraints() [21/29]
|
inherited |
Definition at line 584 of file fe_nedelec_one.C.
◆ compute_constraints() [22/29]
|
inherited |
Definition at line 900 of file fe_lagrange.C.
◆ compute_constraints() [23/29]
|
inherited |
Definition at line 907 of file fe_lagrange.C.
◆ compute_constraints() [24/29]
|
inherited |
◆ compute_constraints() [25/29]
|
inherited |
◆ compute_constraints() [26/29]
|
inherited |
Definition at line 950 of file fe_lagrange_vec.C.
◆ compute_constraints() [27/29]
|
inherited |
Definition at line 959 of file fe_lagrange_vec.C.
◆ compute_constraints() [28/29]
|
inherited |
Definition at line 1287 of file fe_szabab.C.
◆ compute_constraints() [29/29]
|
inherited |
Definition at line 1294 of file fe_szabab.C.
◆ compute_node_constraints()
|
staticinherited |
Computes the nodal constraint contributions (for non-conforming adapted meshes), using Lagrange geometry
Definition at line 820 of file fe_abstract.C.
References std::abs(), libMesh::Elem::build_side_ptr(), libMesh::Elem::default_order(), libMesh::Elem::dim(), libMesh::FEAbstract::fe_type, libMesh::FEInterface::inverse_map(), libMesh::LAGRANGE, libMesh::Elem::level(), libMesh::FEInterface::n_dofs(), libMesh::Elem::neighbor_ptr(), libMesh::Elem::parent(), libMesh::Real, libMesh::remote_elem, libMesh::FEInterface::shape(), libMesh::Elem::side_index_range(), libMesh::Threads::spin_mtx, and libMesh::Elem::subactive().
◆ compute_periodic_constraints()
|
staticinherited |
Computes the constraint matrix contributions (for meshes with periodic boundary conditions) corresponding to variable number var_number, using generic projections.
Definition at line 1650 of file fe_base.C.
References std::abs(), libMesh::TypeVector< T >::absolute_fuzzy_equals(), libMesh::Elem::active(), libMesh::PeriodicBoundaries::boundary(), libMesh::BoundaryInfo::boundary_ids(), libMesh::C_ONE, libMesh::C_ZERO, libMesh::DenseMatrix< T >::cholesky_solve(), libMesh::DofMap::constrain_p_dofs(), libMesh::FEType::default_quadrature_order(), libMesh::Elem::dim(), libMesh::DISCONTINUOUS, libMesh::DofMap::dof_indices(), libMesh::DofObject::dof_number(), libMesh::FEInterface::dofs_on_side(), libMesh::MeshBase::get_boundary_info(), libMesh::PeriodicBoundaryBase::get_corresponding_pos(), libMesh::PeriodicBoundaryBase::get_transformation_matrix(), libMesh::PeriodicBoundaryBase::get_variables(), libMesh::PeriodicBoundaryBase::has_transformation_matrix(), libMesh::Elem::hmin(), libMesh::DofObject::id(), libMesh::index_range(), libMesh::TensorTools::inner_product(), libMesh::DofObject::invalid_id, libMesh::invalid_uint, libMesh::FEInterface::inverse_map(), libMesh::DofMap::is_constrained_dof(), libMesh::Elem::is_edge(), libMesh::Elem::is_face(), libMesh::PeriodicBoundaryBase::is_my_variable(), libMesh::Elem::is_node_on_edge(), libMesh::Elem::is_node_on_side(), libMesh::Elem::is_vertex(), libMesh::Elem::level(), mesh, std::min(), libMesh::Elem::min_p_level_by_neighbor(), libMesh::DofObject::n_comp(), libMesh::Elem::n_edges(), libMesh::Elem::n_nodes(), libMesh::Elem::n_sides(), libMesh::PeriodicBoundaries::neighbor(), libMesh::Elem::neighbor_ptr(), libMesh::Elem::node_ptr(), libMesh::Elem::node_ref(), libMesh::Elem::p_level(), libMesh::PeriodicBoundaryBase::pairedboundary, libMesh::Real, libMesh::DenseVector< T >::resize(), libMesh::DenseMatrix< T >::resize(), libMesh::BoundaryInfo::side_with_boundary_id(), libMesh::Threads::spin_mtx, swap(), libMesh::DofMap::sys_number(), libMesh::TOLERANCE, and libMesh::DofMap::variable_type().
◆ compute_periodic_node_constraints()
|
staticinherited |
Computes the node position constraint equation contributions (for meshes with periodic boundary conditions)
Definition at line 965 of file fe_abstract.C.
References libMesh::Elem::active(), libMesh::PeriodicBoundaries::boundary(), libMesh::Elem::build_side_ptr(), libMesh::Elem::default_order(), libMesh::Elem::dim(), libMesh::FEAbstract::fe_type, libMesh::PeriodicBoundaryBase::get_corresponding_pos(), libMesh::invalid_uint, libMesh::FEInterface::inverse_map(), libMesh::LAGRANGE, libMesh::Elem::level(), mesh, libMesh::FEInterface::n_dofs(), libMesh::PeriodicBoundaries::neighbor(), libMesh::Elem::neighbor_ptr(), libMesh::PeriodicBoundaryBase::pairedboundary, libMesh::Real, libMesh::FEInterface::shape(), libMesh::Elem::side_index_range(), and libMesh::Threads::spin_mtx.
◆ compute_proj_constraints()
|
staticinherited |
Computes the constraint matrix contributions (for non-conforming adapted meshes) corresponding to variable number var_number, using generic projections.
Definition at line 1366 of file fe_base.C.
References std::abs(), libMesh::Elem::active(), libMesh::C_ONE, libMesh::C_ZERO, libMesh::DenseMatrix< T >::cholesky_solve(), libMesh::DofMap::constrain_p_dofs(), libMesh::FEType::default_quadrature_order(), libMesh::Elem::dim(), libMesh::DISCONTINUOUS, libMesh::DofMap::dof_indices(), libMesh::FEInterface::dofs_on_side(), libMesh::OrderWrapper::get_order(), libMesh::TensorTools::inner_product(), libMesh::DofObject::invalid_id, libMesh::FEInterface::inverse_map(), libMesh::DofMap::is_constrained_dof(), libMesh::Elem::level(), std::min(), libMesh::Elem::min_p_level_by_neighbor(), libMesh::Elem::n_neighbors(), libMesh::Elem::n_nodes(), libMesh::Elem::neighbor_ptr(), libMesh::FEType::order, libMesh::Elem::p_level(), libMesh::Real, libMesh::DenseVector< T >::resize(), libMesh::DenseMatrix< T >::resize(), libMesh::Elem::side_index_range(), libMesh::Threads::spin_mtx, libMesh::TOLERANCE, libMesh::DofMap::variable_type(), and libMesh::Elem::which_neighbor_am_i().
◆ compute_shape_functions()
|
protectedvirtualinherited |
After having updated the jacobian and the transformation from local to global coordinates in FEAbstract::compute_map(), the first derivatives of the shape functions are transformed to global coordinates, giving dphi, dphidx, dphidy, and dphidz. This method should rarely be re-defined in derived classes, but still should be usable for children. Therefore, keep it protected.
Implements libMesh::FEAbstract.
Reimplemented in libMesh::FEXYZ< Dim >.
Definition at line 669 of file fe_base.C.
◆ determine_calculations()
|
protectedinherited |
Determine which values are to be calculated, for both the FE itself and for the FEMap.
Definition at line 728 of file fe_base.C.
References libMesh::FEInterface::field_type(), and libMesh::TYPE_VECTOR.
◆ disable_print_counter_info()
|
staticinherited |
Definition at line 106 of file reference_counter.C.
References libMesh::ReferenceCounter::_enable_print_counter.
Referenced by libMesh::LibMeshInit::LibMeshInit().
◆ dofs_on_edge() [1/2]
|
staticinherited |
Fills the vector di with the local degree of freedom indices associated with edge e of element elem
On a p-refined element, o should be the base order of the element.
Definition at line 103 of file fe.C.
◆ dofs_on_edge() [2/2]
|
inherited |
Definition at line 907 of file fe_subdivision_2D.C.
◆ dofs_on_side() [1/2]
|
staticinherited |
Fills the vector di with the local degree of freedom indices associated with side s of element elem
On a p-refined element, o should be the base order of the element.
Definition at line 77 of file fe.C.
◆ dofs_on_side() [2/2]
|
inherited |
Definition at line 906 of file fe_subdivision_2D.C.
◆ edge_reinit() [1/2]
|
overridevirtualinherited |
Reinitializes all the physical element-dependent data based on the edge. The tolerance parameter is passed to the involved call to inverse_map(). By default the shape functions and associated data are computed at the quadrature points specified by the quadrature rule qrule, but may be any points specified on the reference side element specified in the optional argument pts.
Implements libMesh::FEAbstract.
Definition at line 260 of file fe_boundary.C.
◆ edge_reinit() [2/2]
|
virtualinherited |
Reinitializes all the physical element-dependent data based on the edge of the element elem. The tolerance parameter is passed to the involved call to inverse_map(). By default the element data are computed at the quadrature points specified by the quadrature rule qrule, but any set of points on the reference edge element may be specified in the optional argument pts.
Implements libMesh::FEAbstract.
Definition at line 866 of file fe_subdivision_2D.C.
◆ enable_print_counter_info()
|
staticinherited |
Methods to enable/disable the reference counter output from print_info()
Definition at line 100 of file reference_counter.C.
References libMesh::ReferenceCounter::_enable_print_counter.
◆ get_continuity() [1/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 107 of file fe_scalar.C.
◆ get_continuity() [2/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 108 of file fe_scalar.C.
◆ get_continuity() [3/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 109 of file fe_scalar.C.
◆ get_continuity() [4/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 110 of file fe_scalar.C.
◆ get_continuity() [5/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 193 of file fe_l2_hierarchic.C.
◆ get_continuity() [6/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 194 of file fe_l2_hierarchic.C.
◆ get_continuity() [7/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 195 of file fe_l2_hierarchic.C.
◆ get_continuity() [8/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 196 of file fe_l2_hierarchic.C.
◆ get_continuity() [9/54]
|
overridevirtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
◆ get_continuity() [10/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 290 of file fe_clough.C.
◆ get_continuity() [11/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 291 of file fe_clough.C.
◆ get_continuity() [12/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 292 of file fe_clough.C.
◆ get_continuity() [13/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 293 of file fe_clough.C.
◆ get_continuity() [14/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 340 of file fe_hermite.C.
◆ get_continuity() [15/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 341 of file fe_hermite.C.
◆ get_continuity() [16/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 342 of file fe_hermite.C.
◆ get_continuity() [17/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 343 of file fe_hermite.C.
◆ get_continuity() [18/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 369 of file fe_hierarchic.C.
◆ get_continuity() [19/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 370 of file fe_hierarchic.C.
◆ get_continuity() [20/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 371 of file fe_hierarchic.C.
◆ get_continuity() [21/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 372 of file fe_hierarchic.C.
◆ get_continuity() [22/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 402 of file fe_monomial.C.
◆ get_continuity() [23/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 403 of file fe_monomial.C.
◆ get_continuity() [24/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 404 of file fe_monomial.C.
◆ get_continuity() [25/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 405 of file fe_monomial.C.
◆ get_continuity() [26/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 436 of file fe_bernstein.C.
◆ get_continuity() [27/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 437 of file fe_bernstein.C.
◆ get_continuity() [28/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 438 of file fe_bernstein.C.
◆ get_continuity() [29/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 439 of file fe_bernstein.C.
◆ get_continuity() [30/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 474 of file fe_l2_lagrange.C.
◆ get_continuity() [31/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 475 of file fe_l2_lagrange.C.
◆ get_continuity() [32/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 476 of file fe_l2_lagrange.C.
◆ get_continuity() [33/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 477 of file fe_l2_lagrange.C.
◆ get_continuity() [34/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 544 of file fe_nedelec_one.C.
◆ get_continuity() [35/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 545 of file fe_nedelec_one.C.
◆ get_continuity() [36/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 546 of file fe_nedelec_one.C.
◆ get_continuity() [37/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 547 of file fe_nedelec_one.C.
◆ get_continuity() [38/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 877 of file fe_lagrange.C.
◆ get_continuity() [39/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 878 of file fe_lagrange.C.
◆ get_continuity() [40/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 879 of file fe_lagrange.C.
◆ get_continuity() [41/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 880 of file fe_lagrange.C.
◆ get_continuity() [42/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 910 of file fe_subdivision_2D.C.
◆ get_continuity() [43/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 925 of file fe_xyz.C.
◆ get_continuity() [44/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 926 of file fe_xyz.C.
◆ get_continuity() [45/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 927 of file fe_lagrange_vec.C.
◆ get_continuity() [46/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 927 of file fe_xyz.C.
◆ get_continuity() [47/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 928 of file fe_lagrange_vec.C.
◆ get_continuity() [48/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 928 of file fe_xyz.C.
◆ get_continuity() [49/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 929 of file fe_lagrange_vec.C.
◆ get_continuity() [50/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 930 of file fe_lagrange_vec.C.
◆ get_continuity() [51/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 1273 of file fe_szabab.C.
◆ get_continuity() [52/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 1274 of file fe_szabab.C.
◆ get_continuity() [53/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 1275 of file fe_szabab.C.
◆ get_continuity() [54/54]
|
virtualinherited |
- Returns
- The continuity level of the finite element.
Implements libMesh::FEAbstract.
Definition at line 1276 of file fe_szabab.C.
◆ get_curl_phi()
|
inlineinherited |
- Returns
- The curl of the shape function at the quadrature points.
Definition at line 223 of file fe_base.h.
References libMesh::FEAbstract::calculate_curl_phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::curl_phi.
◆ get_curvatures()
|
inlineinherited |
- Returns
- The curvatures for use in face integration.
Definition at line 391 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_d2phi()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 289 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phi.
◆ get_d2phideta2()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points, in reference coordinates
Definition at line 369 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phideta2.
◆ get_d2phidetadzeta()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points, in reference coordinates
Definition at line 377 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidetadzeta.
◆ get_d2phidx2()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 297 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidx2.
◆ get_d2phidxdy()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 305 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidxdy.
◆ get_d2phidxdz()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 313 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidxdz.
◆ get_d2phidxi2()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points, in reference coordinates
Definition at line 345 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidxi2.
◆ get_d2phidxideta()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points, in reference coordinates
Definition at line 353 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidxideta.
◆ get_d2phidxidzeta()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points, in reference coordinates
Definition at line 361 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidxidzeta.
◆ get_d2phidy2()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 321 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidy2.
◆ get_d2phidydz()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 329 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidydz.
◆ get_d2phidz2()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points.
Definition at line 337 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidz2.
◆ get_d2phidzeta2()
|
inlineinherited |
- Returns
- The shape function second derivatives at the quadrature points, in reference coordinates
Definition at line 385 of file fe_base.h.
References libMesh::FEAbstract::calculate_d2phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::d2phidzeta2.
◆ get_d2xyzdeta2()
|
inlineinherited |
- Returns
- The second partial derivatives in eta.
Definition at line 278 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_d2xyzdetadzeta()
|
inlineinherited |
- Returns
- The second partial derivatives in eta-zeta.
Definition at line 308 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_d2xyzdxi2()
|
inlineinherited |
- Returns
- The second partial derivatives in xi.
Definition at line 272 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_d2xyzdxideta()
|
inlineinherited |
- Returns
- The second partial derivatives in xi-eta.
Definition at line 294 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_d2xyzdxidzeta()
|
inlineinherited |
- Returns
- The second partial derivatives in xi-zeta.
Definition at line 302 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_d2xyzdzeta2()
|
inlineinherited |
- Returns
- The second partial derivatives in zeta.
Definition at line 286 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_detadx()
|
inlineinherited |
- Returns
- The deta/dx entry in the transformation matrix from physical to local coordinates.
Definition at line 338 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_detady()
|
inlineinherited |
- Returns
- The deta/dy entry in the transformation matrix from physical to local coordinates.
Definition at line 345 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_detadz()
|
inlineinherited |
- Returns
- The deta/dz entry in the transformation matrix from physical to local coordinates.
Definition at line 352 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dim()
|
inlineinherited |
- Returns
- the dimension of this FE
Definition at line 231 of file fe_abstract.h.
References libMesh::FEAbstract::dim.
◆ get_div_phi()
|
inlineinherited |
- Returns
- The divergence of the shape function at the quadrature points.
Definition at line 231 of file fe_base.h.
References libMesh::FEAbstract::calculate_div_phi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::div_phi.
◆ get_dphase()
|
inlineinherited |
- Returns
- The global first derivative of the phase term which is used in infinite elements, evaluated at the quadrature points.
In case of the general finite element class FE this field is initialized to all zero, so that the variational formulation for an infinite element produces correct element matrices for a mesh using both finite and infinite elements.
Definition at line 403 of file fe_base.h.
References libMesh::FEGenericBase< OutputType >::dphase.
◆ get_dphi()
|
inlineinherited |
- Returns
- The shape function derivatives at the quadrature points.
Definition at line 215 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphi.
◆ get_dphideta()
|
inlineinherited |
- Returns
- The shape function eta-derivative at the quadrature points.
Definition at line 271 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphideta.
◆ get_dphidx()
|
inlineinherited |
- Returns
- The shape function x-derivative at the quadrature points.
Definition at line 239 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphidx.
◆ get_dphidxi()
|
inlineinherited |
- Returns
- The shape function xi-derivative at the quadrature points.
Definition at line 263 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphidxi.
◆ get_dphidy()
|
inlineinherited |
- Returns
- The shape function y-derivative at the quadrature points.
Definition at line 247 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphidy.
◆ get_dphidz()
|
inlineinherited |
- Returns
- The shape function z-derivative at the quadrature points.
Definition at line 255 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphi, libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphidz.
◆ get_dphidzeta()
|
inlineinherited |
- Returns
- The shape function zeta-derivative at the quadrature points.
Definition at line 279 of file fe_base.h.
References libMesh::FEAbstract::calculate_dphiref, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::dphidzeta.
◆ get_dxidx()
|
inlineinherited |
- Returns
- The dxi/dx entry in the transformation matrix from physical to local coordinates.
Definition at line 317 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dxidy()
|
inlineinherited |
- Returns
- The dxi/dy entry in the transformation matrix from physical to local coordinates.
Definition at line 324 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dxidz()
|
inlineinherited |
- Returns
- The dxi/dz entry in the transformation matrix from physical to local coordinates.
Definition at line 331 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dxyzdeta()
|
inlineinherited |
- Returns
- The element tangents in eta-direction at the quadrature points.
Definition at line 259 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dxyzdxi()
|
inlineinherited |
- Returns
- The element tangents in xi-direction at the quadrature points.
Definition at line 252 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dxyzdzeta()
|
inlineinherited |
- Returns
- The element tangents in zeta-direction at the quadrature points.
Definition at line 266 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dzetadx()
|
inlineinherited |
- Returns
- The dzeta/dx entry in the transformation matrix from physical to local coordinates.
Definition at line 359 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dzetady()
|
inlineinherited |
- Returns
- The dzeta/dy entry in the transformation matrix from physical to local coordinates.
Definition at line 366 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_dzetadz()
|
inlineinherited |
- Returns
- The dzeta/dz entry in the transformation matrix from physical to local coordinates.
Definition at line 373 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_family()
|
inlineinherited |
- Returns
- The finite element family of this element.
Definition at line 455 of file fe_abstract.h.
References libMesh::FEType::family, and libMesh::FEAbstract::fe_type.
◆ get_fe_map()
|
inlineinherited |
- Returns
- The mapping object
Definition at line 460 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
Referenced by libMesh::HCurlFETransformation< OutputShape >::init_map_d2phi(), libMesh::H1FETransformation< OutputShape >::init_map_d2phi(), libMesh::HCurlFETransformation< OutputShape >::init_map_dphi(), libMesh::H1FETransformation< OutputShape >::init_map_dphi(), libMesh::HCurlFETransformation< OutputShape >::init_map_phi(), libMesh::HCurlFETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_curl(), libMesh::H1FETransformation< OutputShape >::map_d2phi(), libMesh::H1FETransformation< OutputShape >::map_div(), libMesh::H1FETransformation< OutputShape >::map_dphi(), and libMesh::HCurlFETransformation< OutputShape >::map_phi().
◆ get_fe_type()
|
inlineinherited |
- Returns
- The FE Type (approximation order and family) of the finite element.
Definition at line 429 of file fe_abstract.h.
References libMesh::FEAbstract::fe_type.
Referenced by libMesh::FEMContext::build_new_fe(), libMesh::HCurlFETransformation< OutputShape >::map_phi(), libMesh::H1FETransformation< OutputShape >::map_phi(), libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()(), and libMesh::JumpErrorEstimator::reinit_sides().
◆ get_info()
|
staticinherited |
Gets a string containing the reference information.
Definition at line 47 of file reference_counter.C.
References libMesh::ReferenceCounter::_counts, and libMesh::Quality::name().
Referenced by libMesh::ReferenceCounter::print_info().
◆ get_JxW()
|
inlineinherited |
- Returns
- The element Jacobian times the quadrature weight for each quadrature point.
Definition at line 245 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
Referenced by libMesh::ExactSolution::_compute_error(), libMesh::DiscontinuityMeasure::boundary_side_integration(), libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::System::calculate_norm(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::FEMSystem::init_context(), libMesh::LaplacianErrorEstimator::internal_side_integration(), libMesh::DiscontinuityMeasure::internal_side_integration(), libMesh::KellyErrorEstimator::internal_side_integration(), and libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()().
◆ get_normals()
|
inlineinherited |
- Returns
- The outward pointing normal vectors for face integration.
Definition at line 385 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
Referenced by libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::ParsedFEMFunction< T >::eval_args(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::KellyErrorEstimator::init_context(), and libMesh::KellyErrorEstimator::internal_side_integration().
◆ get_order()
|
inlineinherited |
- Returns
- The approximation order of the finite element.
Definition at line 434 of file fe_abstract.h.
References libMesh::FEAbstract::_p_level, libMesh::FEAbstract::fe_type, and libMesh::FEType::order.
◆ get_p_level()
|
inlineinherited |
- Returns
- The p refinement level that the current shape functions have been calculated for.
Definition at line 424 of file fe_abstract.h.
References libMesh::FEAbstract::_p_level.
◆ get_phi()
|
inlineinherited |
- Returns
- The shape function values at the quadrature points on the element.
Definition at line 207 of file fe_base.h.
References libMesh::FEAbstract::calculate_phi, libMesh::FEAbstract::calculations_started, and libMesh::FEGenericBase< OutputType >::phi.
◆ get_refspace_nodes()
|
staticinherited |
- Returns
- The reference space coordinates of
nodesbased on the element type.
Definition at line 283 of file fe_abstract.C.
References libMesh::EDGE2, libMesh::EDGE3, libMesh::HEX20, libMesh::HEX27, libMesh::HEX8, libMesh::PRISM15, libMesh::PRISM18, libMesh::PRISM6, libMesh::PYRAMID13, libMesh::PYRAMID14, libMesh::PYRAMID5, libMesh::QUAD4, libMesh::QUAD8, libMesh::QUAD9, libMesh::QUADSHELL4, libMesh::QUADSHELL8, libMesh::TET10, libMesh::TET4, libMesh::TRI3, libMesh::TRI6, and libMesh::TRISHELL3.
◆ get_Sobolev_dweight()
|
inlineinherited |
- Returns
- The first global derivative of the multiplicative weight at each quadrature point. See
get_Sobolev_weight()for details. In case ofFEinitialized to all zero.
Definition at line 427 of file fe_base.h.
References libMesh::FEGenericBase< OutputType >::dweight.
◆ get_Sobolev_weight()
|
inlineinherited |
- Returns
- The multiplicative weight at each quadrature point. This weight is used for certain infinite element weak formulations, so that weighted Sobolev spaces are used for the trial function space. This renders the variational form easily computable.
In case of the general finite element class FE this field is initialized to all ones, so that the variational formulation for an infinite element produces correct element matrices for a mesh using both finite and infinite elements.
Definition at line 419 of file fe_base.h.
References libMesh::FEGenericBase< OutputType >::weight.
◆ get_tangents()
|
inlineinherited |
- Returns
- The tangent vectors for face integration.
Definition at line 379 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
◆ get_type()
|
inlineinherited |
- Returns
- The element type that the current shape functions have been calculated for. Useful in determining when shape functions must be recomputed.
Definition at line 418 of file fe_abstract.h.
References libMesh::FEAbstract::elem_type.
◆ get_xyz()
|
inlineinherited |
- Returns
- The
xyzspatial locations of the quadrature points on the element.
Definition at line 238 of file fe_abstract.h.
References libMesh::FEAbstract::_fe_map.
Referenced by libMesh::ExactSolution::_compute_error(), libMesh::DiscontinuityMeasure::boundary_side_integration(), libMesh::KellyErrorEstimator::boundary_side_integration(), libMesh::JumpErrorEstimator::estimate_error(), libMesh::ParsedFEMFunction< T >::eval_args(), libMesh::ExactErrorEstimator::find_squared_element_error(), libMesh::ParsedFEMFunction< T >::init_context(), libMesh::DGFEMContext::neighbor_side_fe_reinit(), and libMesh::GenericProjector< FFunctor, GFunctor, FValue, ProjectionAction >::operator()().
◆ increment_constructor_count()
|
inlineprotectedinherited |
Increments the construction counter. Should be called in the constructor of any derived class that will be reference counted.
Definition at line 181 of file reference_counter.h.
References libMesh::ReferenceCounter::_counts, libMesh::Quality::name(), and libMesh::Threads::spin_mtx.
Referenced by libMesh::ReferenceCountedObject< RBParametrized >::ReferenceCountedObject().
◆ increment_destructor_count()
|
inlineprotectedinherited |
Increments the destruction counter. Should be called in the destructor of any derived class that will be reference counted.
Definition at line 194 of file reference_counter.h.
References libMesh::ReferenceCounter::_counts, libMesh::Quality::name(), and libMesh::Threads::spin_mtx.
Referenced by libMesh::ReferenceCountedObject< RBParametrized >::~ReferenceCountedObject().
◆ init_base_shape_functions()
|
overrideprotectedvirtualinherited |
Initialize the data fields for the base of an an infinite element.
Implements libMesh::FEGenericBase< FEOutputType< T >::type >.
Definition at line 550 of file fe.C.
◆ init_shape_functions()
|
overridevirtual |
Update the various member data fields phi, dphidxi, dphideta, dphidzeta, etc. for the current element. These data will be computed at the points qp, which are generally (but need not be) the quadrature points.
Reimplemented from libMesh::FE< 2, SUBDIVISION >.
Definition at line 404 of file fe_subdivision_2D.C.
References libMesh::FEAbstract::_fe_map, A, libMesh::FEAbstract::calculations_started, libMesh::FEGenericBase< FEOutputType< T >::type >::d2phi, libMesh::FEGenericBase< FEOutputType< T >::type >::d2phideta2, libMesh::FEGenericBase< FEOutputType< T >::type >::d2phidxi2, libMesh::FEGenericBase< FEOutputType< T >::type >::d2phidxideta, libMesh::FEGenericBase< FEOutputType< T >::type >::dphi, libMesh::FEGenericBase< FEOutputType< T >::type >::dphideta, libMesh::FEGenericBase< FEOutputType< T >::type >::dphidxi, libMesh::FEAbstract::fe_type, init_subdivision_matrix(), std::max(), std::min(), libMesh::FEType::order, libMesh::FEGenericBase< FEOutputType< T >::type >::phi, std::pow(), libMesh::Real, libMesh::DenseMatrix< T >::right_multiply(), libMesh::FE< Dim, T >::shape(), libMesh::FE< Dim, T >::shape_deriv(), libMesh::FE< Dim, T >::shape_second_deriv(), libMesh::TRI3SUBDIVISION, and libMesh::Elem::type().
◆ init_subdivision_matrix()
|
static |
Builds the subdivision matrix A for the Loop scheme. The size depends on the element's valence.
Definition at line 42 of file fe_subdivision_2D.C.
References A, and loop_subdivision_mask().
Referenced by init_shape_functions().
◆ inverse_map() [1/4]
|
staticinherited |
- Returns
- The location (on the reference element) of the point
plocated in physical space. This function requires inverting the (possibly nonlinear) transformation map, so it is not trivial. The optional parametertolerancedefines how close is "good enough." The map inversion iteration computes the sequence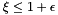 , and the iteration is terminated when
, and the iteration is terminated when 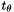
Definition at line 1576 of file fe_map.C.
◆ inverse_map() [2/4]
|
staticinherited |
Takes a number points in physical space (in the physical_points vector) and finds their location on the reference element for the input element elem. The values on the reference element are returned in the vector reference_points. The optional parameter tolerance defines how close is "good enough." The map inversion iteration computes the sequence 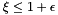 , and the iteration is terminated when
, and the iteration is terminated when 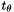
Definition at line 1960 of file fe_map.C.
◆ inverse_map() [3/4]
|
inherited |
Definition at line 876 of file fe_subdivision_2D.C.
◆ inverse_map() [4/4]
|
inherited |
Definition at line 885 of file fe_subdivision_2D.C.
◆ is_hierarchic() [1/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 113 of file fe_scalar.C.
◆ is_hierarchic() [2/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 114 of file fe_scalar.C.
◆ is_hierarchic() [3/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 115 of file fe_scalar.C.
◆ is_hierarchic() [4/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 116 of file fe_scalar.C.
◆ is_hierarchic() [5/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 199 of file fe_l2_hierarchic.C.
◆ is_hierarchic() [6/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 200 of file fe_l2_hierarchic.C.
◆ is_hierarchic() [7/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 201 of file fe_l2_hierarchic.C.
◆ is_hierarchic() [8/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 202 of file fe_l2_hierarchic.C.
◆ is_hierarchic() [9/54]
|
overridevirtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
◆ is_hierarchic() [10/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 296 of file fe_clough.C.
◆ is_hierarchic() [11/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 297 of file fe_clough.C.
◆ is_hierarchic() [12/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 298 of file fe_clough.C.
◆ is_hierarchic() [13/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 299 of file fe_clough.C.
◆ is_hierarchic() [14/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 346 of file fe_hermite.C.
◆ is_hierarchic() [15/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 347 of file fe_hermite.C.
◆ is_hierarchic() [16/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 348 of file fe_hermite.C.
◆ is_hierarchic() [17/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 349 of file fe_hermite.C.
◆ is_hierarchic() [18/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 375 of file fe_hierarchic.C.
◆ is_hierarchic() [19/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 376 of file fe_hierarchic.C.
◆ is_hierarchic() [20/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 377 of file fe_hierarchic.C.
◆ is_hierarchic() [21/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 378 of file fe_hierarchic.C.
◆ is_hierarchic() [22/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 409 of file fe_monomial.C.
◆ is_hierarchic() [23/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 410 of file fe_monomial.C.
◆ is_hierarchic() [24/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 411 of file fe_monomial.C.
◆ is_hierarchic() [25/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 412 of file fe_monomial.C.
◆ is_hierarchic() [26/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 442 of file fe_bernstein.C.
◆ is_hierarchic() [27/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 443 of file fe_bernstein.C.
◆ is_hierarchic() [28/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 444 of file fe_bernstein.C.
◆ is_hierarchic() [29/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 445 of file fe_bernstein.C.
◆ is_hierarchic() [30/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 480 of file fe_l2_lagrange.C.
◆ is_hierarchic() [31/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 481 of file fe_l2_lagrange.C.
◆ is_hierarchic() [32/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 482 of file fe_l2_lagrange.C.
◆ is_hierarchic() [33/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 483 of file fe_l2_lagrange.C.
◆ is_hierarchic() [34/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 550 of file fe_nedelec_one.C.
◆ is_hierarchic() [35/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 551 of file fe_nedelec_one.C.
◆ is_hierarchic() [36/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 552 of file fe_nedelec_one.C.
◆ is_hierarchic() [37/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 553 of file fe_nedelec_one.C.
◆ is_hierarchic() [38/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 883 of file fe_lagrange.C.
◆ is_hierarchic() [39/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 884 of file fe_lagrange.C.
◆ is_hierarchic() [40/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 885 of file fe_lagrange.C.
◆ is_hierarchic() [41/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 886 of file fe_lagrange.C.
◆ is_hierarchic() [42/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 913 of file fe_subdivision_2D.C.
◆ is_hierarchic() [43/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
◆ is_hierarchic() [44/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 933 of file fe_lagrange_vec.C.
◆ is_hierarchic() [45/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
◆ is_hierarchic() [46/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
◆ is_hierarchic() [47/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 934 of file fe_lagrange_vec.C.
◆ is_hierarchic() [48/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 935 of file fe_lagrange_vec.C.
◆ is_hierarchic() [49/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
◆ is_hierarchic() [50/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 936 of file fe_lagrange_vec.C.
◆ is_hierarchic() [51/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 1279 of file fe_szabab.C.
◆ is_hierarchic() [52/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 1280 of file fe_szabab.C.
◆ is_hierarchic() [53/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 1281 of file fe_szabab.C.
◆ is_hierarchic() [54/54]
|
virtualinherited |
- Returns
trueif the finite element's higher order shape functions are hierarchic
Implements libMesh::FEAbstract.
Definition at line 1282 of file fe_szabab.C.
◆ loop_subdivision_mask()
|
static |
Fills the vector weights with the weight coefficients of the Loop subdivision mask for evaluating the limit surface at a node explicitly. The size of weights will be 1 + valence, where valence is the number of neighbor nodes of the node where the limit surface is to be evaluated. The weight for the node itself is the first element of weights.
Definition at line 392 of file fe_subdivision_2D.C.
References libMesh::pi, and libMesh::Real.
Referenced by init_subdivision_matrix().
◆ map()
|
staticinherited |
- Returns
- The location (in physical space) of the point
plocated on the reference element.
Definition at line 1985 of file fe_map.C.
◆ map_eta()
|
staticinherited |
- Returns
- d(xyz)/deta (in physical space) of the point
plocated on the reference element.
Definition at line 2040 of file fe_map.C.
◆ map_xi()
|
staticinherited |
- Returns
- d(xyz)/dxi (in physical space) of the point
plocated on the reference element.
Definition at line 2012 of file fe_map.C.
◆ map_zeta()
|
staticinherited |
- Returns
- d(xyz)/dzeta (in physical space) of the point
plocated on the reference element.
Definition at line 2068 of file fe_map.C.
◆ n_dofs() [1/54]
|
inherited |
Definition at line 87 of file fe_scalar.C.
◆ n_dofs() [2/54]
|
inherited |
Definition at line 88 of file fe_scalar.C.
◆ n_dofs() [3/54]
|
inherited |
Definition at line 89 of file fe_scalar.C.
◆ n_dofs() [4/54]
|
inherited |
Definition at line 90 of file fe_scalar.C.
◆ n_dofs() [5/54]
|
inherited |
Definition at line 174 of file fe_l2_hierarchic.C.
◆ n_dofs() [6/54]
|
inherited |
Definition at line 175 of file fe_l2_hierarchic.C.
◆ n_dofs() [7/54]
|
inherited |
Definition at line 176 of file fe_l2_hierarchic.C.
◆ n_dofs() [8/54]
|
inherited |
Definition at line 177 of file fe_l2_hierarchic.C.
◆ n_dofs() [9/54]
|
staticinherited |
- Returns
- The number of shape functions associated with this finite element.
On a p-refined element, o should be the total order of the element.
◆ n_dofs() [10/54]
|
inherited |
Definition at line 271 of file fe_clough.C.
◆ n_dofs() [11/54]
|
inherited |
Definition at line 272 of file fe_clough.C.
◆ n_dofs() [12/54]
|
inherited |
Definition at line 273 of file fe_clough.C.
◆ n_dofs() [13/54]
|
inherited |
Definition at line 274 of file fe_clough.C.
◆ n_dofs() [14/54]
|
inherited |
Definition at line 321 of file fe_hermite.C.
◆ n_dofs() [15/54]
|
inherited |
Definition at line 322 of file fe_hermite.C.
◆ n_dofs() [16/54]
|
inherited |
Definition at line 323 of file fe_hermite.C.
◆ n_dofs() [17/54]
|
inherited |
Definition at line 324 of file fe_hermite.C.
◆ n_dofs() [18/54]
|
inherited |
Definition at line 351 of file fe_hierarchic.C.
◆ n_dofs() [19/54]
|
inherited |
Definition at line 352 of file fe_hierarchic.C.
◆ n_dofs() [20/54]
|
inherited |
Definition at line 353 of file fe_hierarchic.C.
◆ n_dofs() [21/54]
|
inherited |
Definition at line 354 of file fe_hierarchic.C.
◆ n_dofs() [22/54]
|
inherited |
Definition at line 382 of file fe_monomial.C.
◆ n_dofs() [23/54]
|
inherited |
Definition at line 383 of file fe_monomial.C.
◆ n_dofs() [24/54]
|
inherited |
Definition at line 384 of file fe_monomial.C.
◆ n_dofs() [25/54]
|
inherited |
Definition at line 385 of file fe_monomial.C.
◆ n_dofs() [26/54]
|
inherited |
Definition at line 418 of file fe_bernstein.C.
◆ n_dofs() [27/54]
|
inherited |
Definition at line 419 of file fe_bernstein.C.
◆ n_dofs() [28/54]
|
inherited |
Definition at line 420 of file fe_bernstein.C.
◆ n_dofs() [29/54]
|
inherited |
Definition at line 421 of file fe_bernstein.C.
◆ n_dofs() [30/54]
|
inherited |
Definition at line 454 of file fe_l2_lagrange.C.
◆ n_dofs() [31/54]
|
inherited |
Definition at line 455 of file fe_l2_lagrange.C.
◆ n_dofs() [32/54]
|
inherited |
Definition at line 456 of file fe_l2_lagrange.C.
◆ n_dofs() [33/54]
|
inherited |
Definition at line 457 of file fe_l2_lagrange.C.
◆ n_dofs() [34/54]
|
inherited |
Definition at line 522 of file fe_nedelec_one.C.
◆ n_dofs() [35/54]
|
inherited |
Definition at line 523 of file fe_nedelec_one.C.
◆ n_dofs() [36/54]
|
inherited |
Definition at line 524 of file fe_nedelec_one.C.
◆ n_dofs() [37/54]
|
inherited |
Definition at line 525 of file fe_nedelec_one.C.
◆ n_dofs() [38/54]
|
inherited |
Definition at line 855 of file fe_lagrange.C.
◆ n_dofs() [39/54]
|
inherited |
Definition at line 856 of file fe_lagrange.C.
◆ n_dofs() [40/54]
|
inherited |
Definition at line 857 of file fe_lagrange.C.
◆ n_dofs() [41/54]
|
inherited |
Definition at line 858 of file fe_lagrange.C.
◆ n_dofs() [42/54]
|
inherited |
Definition at line 897 of file fe_subdivision_2D.C.
◆ n_dofs() [43/54]
|
inherited |
Definition at line 905 of file fe_lagrange_vec.C.
◆ n_dofs() [44/54]
|
inherited |
Definition at line 906 of file fe_lagrange_vec.C.
◆ n_dofs() [45/54]
|
inherited |
◆ n_dofs() [46/54]
|
inherited |
Definition at line 907 of file fe_lagrange_vec.C.
◆ n_dofs() [47/54]
|
inherited |
◆ n_dofs() [48/54]
|
inherited |
Definition at line 908 of file fe_lagrange_vec.C.
◆ n_dofs() [49/54]
|
inherited |
◆ n_dofs() [50/54]
|
inherited |
◆ n_dofs() [51/54]
|
inherited |
Definition at line 1255 of file fe_szabab.C.
◆ n_dofs() [52/54]
|
inherited |
Definition at line 1256 of file fe_szabab.C.
◆ n_dofs() [53/54]
|
inherited |
Definition at line 1257 of file fe_szabab.C.
◆ n_dofs() [54/54]
|
inherited |
Definition at line 1258 of file fe_szabab.C.
◆ n_dofs_at_node() [1/54]
|
inherited |
Definition at line 94 of file fe_scalar.C.
◆ n_dofs_at_node() [2/54]
|
inherited |
Definition at line 95 of file fe_scalar.C.
◆ n_dofs_at_node() [3/54]
|
inherited |
Definition at line 96 of file fe_scalar.C.
◆ n_dofs_at_node() [4/54]
|
inherited |
Definition at line 97 of file fe_scalar.C.
◆ n_dofs_at_node() [5/54]
|
inherited |
Definition at line 181 of file fe_l2_hierarchic.C.
◆ n_dofs_at_node() [6/54]
|
inherited |
Definition at line 182 of file fe_l2_hierarchic.C.
◆ n_dofs_at_node() [7/54]
|
inherited |
Definition at line 183 of file fe_l2_hierarchic.C.
◆ n_dofs_at_node() [8/54]
|
inherited |
Definition at line 184 of file fe_l2_hierarchic.C.
◆ n_dofs_at_node() [9/54]
|
staticinherited |
- Returns
- The number of dofs at node
nfor a finite element of typetand ordero.
On a p-refined element, o should be the total order of the element.
◆ n_dofs_at_node() [10/54]
|
inherited |
Definition at line 278 of file fe_clough.C.
◆ n_dofs_at_node() [11/54]
|
inherited |
Definition at line 279 of file fe_clough.C.
◆ n_dofs_at_node() [12/54]
|
inherited |
Definition at line 280 of file fe_clough.C.
◆ n_dofs_at_node() [13/54]
|
inherited |
Definition at line 281 of file fe_clough.C.
◆ n_dofs_at_node() [14/54]
|
inherited |
Definition at line 328 of file fe_hermite.C.
◆ n_dofs_at_node() [15/54]
|
inherited |
Definition at line 329 of file fe_hermite.C.
◆ n_dofs_at_node() [16/54]
|
inherited |
Definition at line 330 of file fe_hermite.C.
◆ n_dofs_at_node() [17/54]
|
inherited |
Definition at line 331 of file fe_hermite.C.
◆ n_dofs_at_node() [18/54]
|
inherited |
Definition at line 357 of file fe_hierarchic.C.
◆ n_dofs_at_node() [19/54]
|
inherited |
Definition at line 358 of file fe_hierarchic.C.
◆ n_dofs_at_node() [20/54]
|
inherited |
Definition at line 359 of file fe_hierarchic.C.
◆ n_dofs_at_node() [21/54]
|
inherited |
Definition at line 360 of file fe_hierarchic.C.
◆ n_dofs_at_node() [22/54]
|
inherited |
Definition at line 389 of file fe_monomial.C.
◆ n_dofs_at_node() [23/54]
|
inherited |
Definition at line 390 of file fe_monomial.C.
◆ n_dofs_at_node() [24/54]
|
inherited |
Definition at line 391 of file fe_monomial.C.
◆ n_dofs_at_node() [25/54]
|
inherited |
Definition at line 392 of file fe_monomial.C.
◆ n_dofs_at_node() [26/54]
|
inherited |
Definition at line 424 of file fe_bernstein.C.
◆ n_dofs_at_node() [27/54]
|
inherited |
Definition at line 425 of file fe_bernstein.C.
◆ n_dofs_at_node() [28/54]
|
inherited |
Definition at line 426 of file fe_bernstein.C.
◆ n_dofs_at_node() [29/54]
|
inherited |
Definition at line 427 of file fe_bernstein.C.
◆ n_dofs_at_node() [30/54]
|
inherited |
Definition at line 461 of file fe_l2_lagrange.C.
◆ n_dofs_at_node() [31/54]
|
inherited |
Definition at line 462 of file fe_l2_lagrange.C.
◆ n_dofs_at_node() [32/54]
|
inherited |
Definition at line 463 of file fe_l2_lagrange.C.
◆ n_dofs_at_node() [33/54]
|
inherited |
Definition at line 464 of file fe_l2_lagrange.C.
◆ n_dofs_at_node() [34/54]
|
inherited |
Definition at line 530 of file fe_nedelec_one.C.
◆ n_dofs_at_node() [35/54]
|
inherited |
Definition at line 531 of file fe_nedelec_one.C.
◆ n_dofs_at_node() [36/54]
|
inherited |
Definition at line 532 of file fe_nedelec_one.C.
◆ n_dofs_at_node() [37/54]
|
inherited |
Definition at line 533 of file fe_nedelec_one.C.
◆ n_dofs_at_node() [38/54]
|
inherited |
Definition at line 863 of file fe_lagrange.C.
◆ n_dofs_at_node() [39/54]
|
inherited |
Definition at line 864 of file fe_lagrange.C.
◆ n_dofs_at_node() [40/54]
|
inherited |
Definition at line 865 of file fe_lagrange.C.
◆ n_dofs_at_node() [41/54]
|
inherited |
Definition at line 866 of file fe_lagrange.C.
◆ n_dofs_at_node() [42/54]
|
inherited |
Definition at line 900 of file fe_subdivision_2D.C.
◆ n_dofs_at_node() [43/54]
|
inherited |
Definition at line 913 of file fe_lagrange_vec.C.
◆ n_dofs_at_node() [44/54]
|
inherited |
◆ n_dofs_at_node() [45/54]
|
inherited |
Definition at line 914 of file fe_lagrange_vec.C.
◆ n_dofs_at_node() [46/54]
|
inherited |
◆ n_dofs_at_node() [47/54]
|
inherited |
Definition at line 915 of file fe_lagrange_vec.C.
◆ n_dofs_at_node() [48/54]
|
inherited |
◆ n_dofs_at_node() [49/54]
|
inherited |
Definition at line 916 of file fe_lagrange_vec.C.
◆ n_dofs_at_node() [50/54]
|
inherited |
◆ n_dofs_at_node() [51/54]
|
inherited |
Definition at line 1261 of file fe_szabab.C.
◆ n_dofs_at_node() [52/54]
|
inherited |
Definition at line 1262 of file fe_szabab.C.
◆ n_dofs_at_node() [53/54]
|
inherited |
Definition at line 1263 of file fe_szabab.C.
◆ n_dofs_at_node() [54/54]
|
inherited |
Definition at line 1264 of file fe_szabab.C.
◆ n_dofs_per_elem() [1/54]
|
inherited |
Definition at line 101 of file fe_scalar.C.
◆ n_dofs_per_elem() [2/54]
|
inherited |
Definition at line 102 of file fe_scalar.C.
◆ n_dofs_per_elem() [3/54]
|
inherited |
Definition at line 103 of file fe_scalar.C.
◆ n_dofs_per_elem() [4/54]
|
inherited |
Definition at line 104 of file fe_scalar.C.
◆ n_dofs_per_elem() [5/54]
|
inherited |
Definition at line 187 of file fe_l2_hierarchic.C.
◆ n_dofs_per_elem() [6/54]
|
inherited |
Definition at line 188 of file fe_l2_hierarchic.C.
◆ n_dofs_per_elem() [7/54]
|
inherited |
Definition at line 189 of file fe_l2_hierarchic.C.
◆ n_dofs_per_elem() [8/54]
|
inherited |
Definition at line 190 of file fe_l2_hierarchic.C.
◆ n_dofs_per_elem() [9/54]
|
staticinherited |
- Returns
- The number of dofs interior to the element, not associated with any interior nodes.
On a p-refined element, o should be the total order of the element.
◆ n_dofs_per_elem() [10/54]
|
inherited |
Definition at line 284 of file fe_clough.C.
◆ n_dofs_per_elem() [11/54]
|
inherited |
Definition at line 285 of file fe_clough.C.
◆ n_dofs_per_elem() [12/54]
|
inherited |
Definition at line 286 of file fe_clough.C.
◆ n_dofs_per_elem() [13/54]
|
inherited |
Definition at line 287 of file fe_clough.C.
◆ n_dofs_per_elem() [14/54]
|
inherited |
Definition at line 334 of file fe_hermite.C.
◆ n_dofs_per_elem() [15/54]
|
inherited |
Definition at line 335 of file fe_hermite.C.
◆ n_dofs_per_elem() [16/54]
|
inherited |
Definition at line 336 of file fe_hermite.C.
◆ n_dofs_per_elem() [17/54]
|
inherited |
Definition at line 337 of file fe_hermite.C.
◆ n_dofs_per_elem() [18/54]
|
inherited |
Definition at line 363 of file fe_hierarchic.C.
◆ n_dofs_per_elem() [19/54]
|
inherited |
Definition at line 364 of file fe_hierarchic.C.
◆ n_dofs_per_elem() [20/54]
|
inherited |
Definition at line 365 of file fe_hierarchic.C.
◆ n_dofs_per_elem() [21/54]
|
inherited |
Definition at line 366 of file fe_hierarchic.C.
◆ n_dofs_per_elem() [22/54]
|
inherited |
Definition at line 395 of file fe_monomial.C.
◆ n_dofs_per_elem() [23/54]
|
inherited |
Definition at line 396 of file fe_monomial.C.
◆ n_dofs_per_elem() [24/54]
|
inherited |
Definition at line 397 of file fe_monomial.C.
◆ n_dofs_per_elem() [25/54]
|
inherited |
Definition at line 398 of file fe_monomial.C.
◆ n_dofs_per_elem() [26/54]
|
inherited |
Definition at line 430 of file fe_bernstein.C.
◆ n_dofs_per_elem() [27/54]
|
inherited |
Definition at line 431 of file fe_bernstein.C.
◆ n_dofs_per_elem() [28/54]
|
inherited |
Definition at line 432 of file fe_bernstein.C.
◆ n_dofs_per_elem() [29/54]
|
inherited |
Definition at line 433 of file fe_bernstein.C.
◆ n_dofs_per_elem() [30/54]
|
inherited |
Definition at line 468 of file fe_l2_lagrange.C.
◆ n_dofs_per_elem() [31/54]
|
inherited |
Definition at line 469 of file fe_l2_lagrange.C.
◆ n_dofs_per_elem() [32/54]
|
inherited |
Definition at line 470 of file fe_l2_lagrange.C.
◆ n_dofs_per_elem() [33/54]
|
inherited |
Definition at line 471 of file fe_l2_lagrange.C.
◆ n_dofs_per_elem() [34/54]
|
inherited |
Definition at line 538 of file fe_nedelec_one.C.
◆ n_dofs_per_elem() [35/54]
|
inherited |
Definition at line 539 of file fe_nedelec_one.C.
◆ n_dofs_per_elem() [36/54]
|
inherited |
Definition at line 540 of file fe_nedelec_one.C.
◆ n_dofs_per_elem() [37/54]
|
inherited |
Definition at line 541 of file fe_nedelec_one.C.
◆ n_dofs_per_elem() [38/54]
|
inherited |
Definition at line 871 of file fe_lagrange.C.
◆ n_dofs_per_elem() [39/54]
|
inherited |
Definition at line 872 of file fe_lagrange.C.
◆ n_dofs_per_elem() [40/54]
|
inherited |
Definition at line 873 of file fe_lagrange.C.
◆ n_dofs_per_elem() [41/54]
|
inherited |
Definition at line 874 of file fe_lagrange.C.
◆ n_dofs_per_elem() [42/54]
|
inherited |
Definition at line 903 of file fe_subdivision_2D.C.
◆ n_dofs_per_elem() [43/54]
|
inherited |
◆ n_dofs_per_elem() [44/54]
|
inherited |
◆ n_dofs_per_elem() [45/54]
|
inherited |
Definition at line 921 of file fe_lagrange_vec.C.
◆ n_dofs_per_elem() [46/54]
|
inherited |
◆ n_dofs_per_elem() [47/54]
|
inherited |
Definition at line 922 of file fe_lagrange_vec.C.
◆ n_dofs_per_elem() [48/54]
|
inherited |
◆ n_dofs_per_elem() [49/54]
|
inherited |
Definition at line 923 of file fe_lagrange_vec.C.
◆ n_dofs_per_elem() [50/54]
|
inherited |
Definition at line 924 of file fe_lagrange_vec.C.
◆ n_dofs_per_elem() [51/54]
|
inherited |
Definition at line 1267 of file fe_szabab.C.
◆ n_dofs_per_elem() [52/54]
|
inherited |
Definition at line 1268 of file fe_szabab.C.
◆ n_dofs_per_elem() [53/54]
|
inherited |
Definition at line 1269 of file fe_szabab.C.
◆ n_dofs_per_elem() [54/54]
|
inherited |
Definition at line 1270 of file fe_szabab.C.
◆ n_objects()
|
inlinestaticinherited |
Prints the number of outstanding (created, but not yet destroyed) objects.
Definition at line 83 of file reference_counter.h.
References libMesh::ReferenceCounter::_n_objects.
◆ n_quadrature_points()
|
overridevirtualinherited |
- Returns
- The total number of quadrature points. Call this to get an upper bound for the
forloop in your simulation for matrix assembly of the current element.
Implements libMesh::FEAbstract.
Definition at line 69 of file fe.C.
◆ n_shape_functions() [1/2]
|
overridevirtualinherited |
- Returns
- The number of shape functions associated with this finite element.
Implements libMesh::FEAbstract.
Definition at line 50 of file fe.C.
◆ n_shape_functions() [2/2]
|
inlinestaticinherited |
◆ nodal_soln() [1/54]
|
inherited |
Definition at line 58 of file fe_scalar.C.
◆ nodal_soln() [2/54]
|
inherited |
Definition at line 65 of file fe_scalar.C.
◆ nodal_soln() [3/54]
|
inherited |
Definition at line 72 of file fe_scalar.C.
◆ nodal_soln() [4/54]
|
inherited |
Definition at line 79 of file fe_scalar.C.
◆ nodal_soln() [5/54]
|
inherited |
Definition at line 146 of file fe_l2_hierarchic.C.
◆ nodal_soln() [6/54]
|
inherited |
Definition at line 153 of file fe_l2_hierarchic.C.
◆ nodal_soln() [7/54]
|
inherited |
Definition at line 160 of file fe_l2_hierarchic.C.
◆ nodal_soln() [8/54]
|
inherited |
Definition at line 167 of file fe_l2_hierarchic.C.
◆ nodal_soln() [9/54]
|
staticinherited |
Build the nodal soln from the element soln. This is the solution that will be plotted.
On a p-refined element, o should be the base order of the element.
◆ nodal_soln() [10/54]
|
inherited |
Definition at line 242 of file fe_clough.C.
◆ nodal_soln() [11/54]
|
inherited |
Definition at line 249 of file fe_clough.C.
◆ nodal_soln() [12/54]
|
inherited |
Definition at line 256 of file fe_clough.C.
◆ nodal_soln() [13/54]
|
inherited |
Definition at line 263 of file fe_clough.C.
◆ nodal_soln() [14/54]
|
inherited |
Definition at line 288 of file fe_hermite.C.
◆ nodal_soln() [15/54]
|
inherited |
Definition at line 295 of file fe_hermite.C.
◆ nodal_soln() [16/54]
|
inherited |
Definition at line 302 of file fe_hermite.C.
◆ nodal_soln() [17/54]
|
inherited |
Definition at line 309 of file fe_hermite.C.
◆ nodal_soln() [18/54]
|
inherited |
Definition at line 322 of file fe_hierarchic.C.
◆ nodal_soln() [19/54]
|
inherited |
Definition at line 329 of file fe_hierarchic.C.
◆ nodal_soln() [20/54]
|
inherited |
Definition at line 336 of file fe_hierarchic.C.
◆ nodal_soln() [21/54]
|
inherited |
Definition at line 343 of file fe_hierarchic.C.
◆ nodal_soln() [22/54]
|
inherited |
Definition at line 353 of file fe_monomial.C.
◆ nodal_soln() [23/54]
|
inherited |
Definition at line 360 of file fe_monomial.C.
◆ nodal_soln() [24/54]
|
inherited |
Definition at line 367 of file fe_monomial.C.
◆ nodal_soln() [25/54]
|
inherited |
Definition at line 374 of file fe_monomial.C.
◆ nodal_soln() [26/54]
|
inherited |
Definition at line 389 of file fe_bernstein.C.
◆ nodal_soln() [27/54]
|
inherited |
Definition at line 396 of file fe_bernstein.C.
◆ nodal_soln() [28/54]
|
inherited |
Definition at line 403 of file fe_bernstein.C.
◆ nodal_soln() [29/54]
|
inherited |
Definition at line 410 of file fe_bernstein.C.
◆ nodal_soln() [30/54]
|
inherited |
Definition at line 423 of file fe_l2_lagrange.C.
◆ nodal_soln() [31/54]
|
inherited |
Definition at line 430 of file fe_l2_lagrange.C.
◆ nodal_soln() [32/54]
|
inherited |
Definition at line 437 of file fe_l2_lagrange.C.
◆ nodal_soln() [33/54]
|
inherited |
Definition at line 444 of file fe_l2_lagrange.C.
◆ nodal_soln() [34/54]
|
inherited |
Definition at line 491 of file fe_nedelec_one.C.
◆ nodal_soln() [35/54]
|
inherited |
Definition at line 498 of file fe_nedelec_one.C.
◆ nodal_soln() [36/54]
|
inherited |
Definition at line 505 of file fe_nedelec_one.C.
◆ nodal_soln() [37/54]
|
inherited |
Definition at line 507 of file fe_lagrange_vec.C.
◆ nodal_soln() [38/54]
|
inherited |
Definition at line 512 of file fe_nedelec_one.C.
◆ nodal_soln() [39/54]
|
inherited |
Definition at line 514 of file fe_lagrange_vec.C.
◆ nodal_soln() [40/54]
|
inherited |
Definition at line 521 of file fe_lagrange_vec.C.
◆ nodal_soln() [41/54]
|
inherited |
Definition at line 528 of file fe_lagrange_vec.C.
◆ nodal_soln() [42/54]
|
inherited |
Definition at line 818 of file fe_subdivision_2D.C.
◆ nodal_soln() [43/54]
|
inherited |
Definition at line 824 of file fe_lagrange.C.
◆ nodal_soln() [44/54]
|
inherited |
Definition at line 831 of file fe_lagrange.C.
◆ nodal_soln() [45/54]
|
inherited |
Definition at line 838 of file fe_lagrange.C.
◆ nodal_soln() [46/54]
|
inherited |
Definition at line 845 of file fe_lagrange.C.
◆ nodal_soln() [47/54]
|
inherited |
◆ nodal_soln() [48/54]
|
inherited |
◆ nodal_soln() [49/54]
|
inherited |
◆ nodal_soln() [50/54]
|
inherited |
◆ nodal_soln() [51/54]
|
inherited |
Definition at line 1226 of file fe_szabab.C.
◆ nodal_soln() [52/54]
|
inherited |
Definition at line 1233 of file fe_szabab.C.
◆ nodal_soln() [53/54]
|
inherited |
Definition at line 1240 of file fe_szabab.C.
◆ nodal_soln() [54/54]
|
inherited |
Definition at line 1247 of file fe_szabab.C.
◆ on_reference_element()
|
staticinherited |
- Returns
trueif the point p is located on the reference element for element type t, false otherwise. Since we are doing floating point comparisons here the parameterepscan be specified to indicate a tolerance. For example,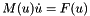 becomes
becomes 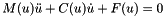 .
.
Definition at line 581 of file fe_abstract.C.
References libMesh::EDGE2, libMesh::EDGE3, libMesh::EDGE4, libMesh::HEX20, libMesh::HEX27, libMesh::HEX8, libMesh::INFHEX16, libMesh::INFHEX18, libMesh::INFHEX8, libMesh::INFPRISM12, libMesh::INFPRISM6, libMesh::NODEELEM, libMesh::PRISM15, libMesh::PRISM18, libMesh::PRISM6, libMesh::PYRAMID13, libMesh::PYRAMID14, libMesh::PYRAMID5, libMesh::QUAD4, libMesh::QUAD8, libMesh::QUAD9, libMesh::QUADSHELL4, libMesh::QUADSHELL8, libMesh::Real, libMesh::TET10, libMesh::TET4, libMesh::TRI3, libMesh::TRI6, and libMesh::TRISHELL3.
Referenced by libMesh::FEInterface::ifem_on_reference_element(), libMesh::FE< Dim, LAGRANGE_VEC >::inverse_map(), and libMesh::FEInterface::on_reference_element().
◆ print_d2phi()
|
virtualinherited |
Prints the value of each shape function's second derivatives at each quadrature point.
Implements libMesh::FEAbstract.
Definition at line 776 of file fe_base.C.
References libMesh::index_range().
◆ print_dphi()
|
virtualinherited |
Prints the value of each shape function's derivative at each quadrature point.
Implements libMesh::FEAbstract.
Definition at line 718 of file fe_base.C.
References libMesh::index_range().
◆ print_info() [1/2]
|
staticinherited |
Prints the reference information, by default to libMesh::out.
Definition at line 87 of file reference_counter.C.
References libMesh::ReferenceCounter::_enable_print_counter, and libMesh::ReferenceCounter::get_info().
◆ print_info() [2/2]
|
inherited |
Prints all the relevant information about the current element.
Definition at line 793 of file fe_abstract.C.
References libMesh::FEAbstract::print_dphi(), libMesh::FEAbstract::print_JxW(), libMesh::FEAbstract::print_phi(), and libMesh::FEAbstract::print_xyz().
Referenced by libMesh::operator<<().
◆ print_JxW()
|
inherited |
Prints the Jacobian times the weight for each quadrature point.
Definition at line 780 of file fe_abstract.C.
References libMesh::FEAbstract::_fe_map.
Referenced by libMesh::FEAbstract::print_info().
◆ print_phi()
|
virtualinherited |
Prints the value of each shape function at each quadrature point.
Implements libMesh::FEAbstract.
Definition at line 707 of file fe_base.C.
References libMesh::index_range().
◆ print_xyz()
|
inherited |
Prints the spatial location of each quadrature point (on the physical element).
Definition at line 787 of file fe_abstract.C.
References libMesh::FEAbstract::_fe_map.
Referenced by libMesh::FEAbstract::print_info().
◆ regular_shape()
|
static |
- Returns
- The value of the
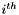 of the 12 quartic box splines interpolating a regular Loop subdivision element, evaluated at the barycentric coordinates
of the 12 quartic box splines interpolating a regular Loop subdivision element, evaluated at the barycentric coordinates v,w.
Definition at line 134 of file fe_subdivision_2D.C.
References libMesh::Utility::pow(), and libMesh::Real.
◆ regular_shape_deriv()
|
static |
- Returns
- The
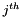 derivative of the
derivative of the 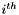 of the 12 quartic box splines interpolating a regular Loop subdivision element, evaluated at the barycentric coordinates
of the 12 quartic box splines interpolating a regular Loop subdivision element, evaluated at the barycentric coordinates v,w.
Definition at line 190 of file fe_subdivision_2D.C.
References libMesh::Real.
◆ regular_shape_second_deriv()
|
static |
- Returns
- The second
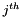 derivative of the
derivative of the 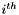 of the 12 quartic box splines interpolating a regular Loop subdivision element, evaluated at the barycentric coordinates
of the 12 quartic box splines interpolating a regular Loop subdivision element, evaluated at the barycentric coordinates v,w.
Definition at line 279 of file fe_subdivision_2D.C.
References libMesh::Real.
◆ reinit() [1/2]
|
overridevirtual |
This is at the core of this class. Use this for each new non-ghosted element in the mesh. Reinitializes all the physical element-dependent data based on the current element elem. By default the shape functions and associated data are computed at the quadrature points specified by the quadrature rule qrule, but may be any points specified on the reference element specified in the optional argument pts.
Reimplemented from libMesh::FE< 2, SUBDIVISION >.
◆ reinit() [2/2]
|
inlineoverridevirtual |
This prevents some compilers being confused by partially overriding this virtual function.
Reimplemented from libMesh::FE< 2, SUBDIVISION >.
◆ set_fe_order()
|
inlineinherited |
Sets the base FE order of the finite element.
Definition at line 439 of file fe_abstract.h.
References libMesh::FEAbstract::fe_type, and libMesh::FEType::order.
◆ shape() [1/109]
|
inherited |
Definition at line 29 of file fe_scalar_shape_3D.C.
◆ shape() [2/109]
|
inherited |
Definition at line 29 of file fe_scalar_shape_2D.C.
◆ shape() [3/109]
|
inherited |
Definition at line 29 of file fe_nedelec_one_shape_2D.C.
◆ shape() [4/109]
|
inherited |
Definition at line 29 of file fe_nedelec_one_shape_3D.C.
◆ shape() [5/109]
|
inherited |
Definition at line 29 of file fe_scalar_shape_0D.C.
◆ shape() [6/109]
|
inherited |
Definition at line 29 of file fe_scalar_shape_1D.C.
◆ shape() [7/109]
|
inherited |
Definition at line 32 of file fe_lagrange_shape_2D.C.
◆ shape() [8/109]
|
inherited |
Definition at line 32 of file fe_lagrange_shape_1D.C.
◆ shape() [9/109]
|
inherited |
Definition at line 32 of file fe_l2_hierarchic_shape_2D.C.
◆ shape() [10/109]
|
inherited |
Definition at line 32 of file fe_bernstein_shape_0D.C.
◆ shape() [11/109]
|
inherited |
Definition at line 32 of file fe_l2_lagrange_shape_0D.C.
◆ shape() [12/109]
|
inherited |
Definition at line 32 of file fe_hierarchic_shape_0D.C.
◆ shape() [13/109]
|
inherited |
Definition at line 32 of file fe_hierarchic_shape_2D.C.
◆ shape() [14/109]
|
inherited |
Definition at line 32 of file fe_monomial_shape_0D.C.
◆ shape() [15/109]
|
inherited |
Definition at line 32 of file fe_monomial_shape_1D.C.
◆ shape() [16/109]
|
inherited |
Definition at line 32 of file fe_monomial_shape_2D.C.
◆ shape() [17/109]
|
inherited |
Definition at line 32 of file fe_clough_shape_0D.C.
◆ shape() [18/109]
|
inherited |
Definition at line 32 of file fe_monomial_shape_3D.C.
◆ shape() [19/109]
|
inherited |
Definition at line 32 of file fe_l2_hierarchic_shape_0D.C.
◆ shape() [20/109]
|
inherited |
Definition at line 32 of file fe_szabab_shape_0D.C.
◆ shape() [21/109]
|
inherited |
Definition at line 32 of file fe_lagrange_shape_3D.C.
◆ shape() [22/109]
|
inherited |
Definition at line 32 of file fe_szabab_shape_3D.C.
◆ shape() [23/109]
|
inherited |
Definition at line 32 of file fe_l2_lagrange_shape_1D.C.
◆ shape() [24/109]
|
inherited |
Definition at line 32 of file fe_xyz_shape_0D.C.
◆ shape() [25/109]
|
inherited |
Definition at line 32 of file fe_xyz_shape_1D.C.
◆ shape() [26/109]
|
inherited |
Definition at line 32 of file fe_hermite_shape_0D.C.
◆ shape() [27/109]
|
inherited |
Definition at line 32 of file fe_l2_lagrange_shape_2D.C.
◆ shape() [28/109]
|
inherited |
Definition at line 32 of file fe_xyz_shape_2D.C.
◆ shape() [29/109]
|
inherited |
Definition at line 32 of file fe_xyz_shape_3D.C.
◆ shape() [30/109]
|
inherited |
Definition at line 32 of file fe_l2_lagrange_shape_3D.C.
◆ shape() [31/109]
|
inherited |
Definition at line 32 of file fe_lagrange_shape_0D.C.
◆ shape() [32/109]
|
inherited |
Definition at line 33 of file fe_clough_shape_3D.C.
◆ shape() [33/109]
|
inherited |
Definition at line 33 of file fe_hierarchic_shape_1D.C.
◆ shape() [34/109]
|
inherited |
Definition at line 33 of file fe_l2_hierarchic_shape_1D.C.
◆ shape() [35/109]
|
inherited |
Definition at line 34 of file fe_bernstein_shape_2D.C.
◆ shape() [36/109]
|
inherited |
Definition at line 35 of file fe_szabab_shape_1D.C.
◆ shape() [37/109]
|
inherited |
Definition at line 36 of file fe_bernstein_shape_3D.C.
◆ shape() [38/109]
|
inherited |
Definition at line 38 of file fe_scalar_shape_2D.C.
◆ shape() [39/109]
|
inherited |
Definition at line 38 of file fe_scalar_shape_3D.C.
◆ shape() [40/109]
|
inherited |
Definition at line 38 of file fe_scalar_shape_0D.C.
◆ shape() [41/109]
|
inherited |
Definition at line 38 of file fe_scalar_shape_1D.C.
◆ shape() [42/109]
|
inherited |
Definition at line 38 of file fe_bernstein_shape_1D.C.
◆ shape() [43/109]
|
inherited |
Definition at line 41 of file fe_nedelec_one_shape_3D.C.
◆ shape() [44/109]
|
inherited |
Definition at line 42 of file fe_nedelec_one_shape_2D.C.
◆ shape() [45/109]
|
inherited |
Definition at line 44 of file fe_l2_hierarchic_shape_2D.C.
◆ shape() [46/109]
|
inherited |
Definition at line 44 of file fe_clough_shape_0D.C.
◆ shape() [47/109]
|
inherited |
Definition at line 44 of file fe_hierarchic_shape_0D.C.
◆ shape() [48/109]
|
inherited |
Definition at line 44 of file fe_monomial_shape_0D.C.
◆ shape() [49/109]
|
inherited |
Definition at line 44 of file fe_hierarchic_shape_2D.C.
◆ shape() [50/109]
|
inherited |
Definition at line 44 of file fe_szabab_shape_0D.C.
◆ shape() [51/109]
|
inherited |
Definition at line 44 of file fe_bernstein_shape_0D.C.
◆ shape() [52/109]
|
inherited |
Definition at line 44 of file fe_l2_hierarchic_shape_0D.C.
◆ shape() [53/109]
|
inherited |
Definition at line 44 of file fe_l2_lagrange_shape_0D.C.
◆ shape() [54/109]
|
inherited |
Definition at line 44 of file fe_szabab_shape_3D.C.
◆ shape() [55/109]
|
inherited |
Definition at line 44 of file fe_xyz_shape_0D.C.
◆ shape() [56/109]
|
inherited |
Definition at line 44 of file fe_xyz_shape_1D.C.
◆ shape() [57/109]
|
inherited |
Definition at line 44 of file fe_xyz_shape_2D.C.
◆ shape() [58/109]
|
inherited |
Definition at line 44 of file fe_hermite_shape_0D.C.
◆ shape() [59/109]
|
inherited |
Definition at line 44 of file fe_xyz_shape_3D.C.
◆ shape() [60/109]
|
inherited |
Definition at line 44 of file fe_lagrange_shape_0D.C.
◆ shape() [61/109]
|
inherited |
Definition at line 45 of file fe_clough_shape_3D.C.
◆ shape() [62/109]
|
inherited |
Definition at line 46 of file fe_bernstein_shape_2D.C.
◆ shape() [63/109]
|
inherited |
Definition at line 48 of file fe_bernstein_shape_3D.C.
◆ shape() [64/109]
|
inherited |
Definition at line 53 of file fe_szabab_shape_2D.C.
◆ shape() [65/109]
|
inherited |
Definition at line 65 of file fe_szabab_shape_2D.C.
◆ shape() [66/109]
|
inherited |
Definition at line 70 of file fe_monomial_shape_1D.C.
◆ shape() [67/109]
|
inherited |
Definition at line 79 of file fe_szabab_shape_1D.C.
◆ shape() [68/109]
|
inherited |
Definition at line 101 of file fe_l2_hierarchic_shape_1D.C.
◆ shape() [69/109]
|
inherited |
Definition at line 101 of file fe_hierarchic_shape_1D.C.
◆ shape() [70/109]
|
staticinherited |
- Returns
- The value of the
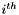 shape function at point
shape function at point p. This method allows you to specify the dimension, element type, and order directly. This allows the method to be static.
On a p-refined element, o should be the total order of the element.
◆ shape() [71/109]
|
inherited |
Definition at line 117 of file fe_l2_lagrange_shape_1D.C.
◆ shape() [72/109]
|
inherited |
Definition at line 117 of file fe_lagrange_shape_1D.C.
◆ shape() [73/109]
|
inherited |
Definition at line 118 of file fe_monomial_shape_2D.C.
◆ shape() [74/109]
|
staticinherited |
- Returns
- The value of the
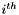 shape function at point
shape function at point p. This method allows you to specify the dimension, element type, and order directly. This allows the method to be static.
On a p-refined element, o should be the base order of the element.
◆ shape() [75/109]
|
inherited |
Definition at line 175 of file fe_hermite_shape_1D.C.
◆ shape() [76/109]
|
inherited |
Definition at line 186 of file fe_monomial_shape_3D.C.
◆ shape() [77/109]
|
inherited |
Definition at line 187 of file fe_hermite_shape_1D.C.
◆ shape() [78/109]
|
inherited |
Definition at line 189 of file fe_hermite_shape_2D.C.
◆ shape() [79/109]
|
inherited |
Definition at line 190 of file fe_bernstein_shape_1D.C.
◆ shape() [80/109]
|
inherited |
Definition at line 201 of file fe_hermite_shape_2D.C.
◆ shape() [81/109]
|
inherited |
Definition at line 208 of file fe_l2_lagrange_shape_2D.C.
◆ shape() [82/109]
|
inherited |
Definition at line 210 of file fe_lagrange_shape_2D.C.
◆ shape() [83/109]
|
inherited |
Definition at line 211 of file fe_clough_shape_1D.C.
◆ shape() [84/109]
|
inherited |
Definition at line 223 of file fe_clough_shape_1D.C.
◆ shape() [85/109]
|
inherited |
Definition at line 356 of file fe_l2_lagrange_shape_3D.C.
◆ shape() [86/109]
|
inherited |
Definition at line 376 of file fe_hermite_shape_3D.C.
◆ shape() [87/109]
|
inherited |
Definition at line 388 of file fe_hermite_shape_3D.C.
◆ shape() [88/109]
|
inherited |
Definition at line 538 of file fe_lagrange_vec.C.
◆ shape() [89/109]
|
inherited |
Subdivision finite elements.
Template specialization prototypes are needed for calling from inside FESubdivision::init_shape_functions
◆ shape() [90/109]
|
inherited |
Definition at line 558 of file fe_lagrange_shape_3D.C.
◆ shape() [91/109]
|
inherited |
Definition at line 560 of file fe_lagrange_vec.C.
◆ shape() [92/109]
|
inherited |
Definition at line 582 of file fe_lagrange_vec.C.
◆ shape() [93/109]
|
inherited |
Definition at line 593 of file fe_nedelec_one.C.
◆ shape() [94/109]
|
inherited |
Definition at line 596 of file fe_nedelec_one.C.
◆ shape() [95/109]
|
inherited |
Definition at line 616 of file fe_nedelec_one.C.
◆ shape() [96/109]
|
inherited |
Definition at line 619 of file fe_nedelec_one.C.
◆ shape() [97/109]
|
inherited |
Definition at line 645 of file fe_l2_hierarchic_shape_3D.C.
◆ shape() [98/109]
|
inherited |
Definition at line 645 of file fe_hierarchic_shape_3D.C.
◆ shape() [99/109]
|
inherited |
Definition at line 647 of file fe_lagrange_vec.C.
◆ shape() [100/109]
|
inherited |
Definition at line 657 of file fe_hierarchic_shape_3D.C.
◆ shape() [101/109]
|
inherited |
Definition at line 657 of file fe_l2_hierarchic_shape_3D.C.
◆ shape() [102/109]
|
inherited |
Definition at line 700 of file fe_subdivision_2D.C.
◆ shape() [103/109]
|
inherited |
Definition at line 722 of file fe_lagrange_vec.C.
◆ shape() [104/109]
|
inherited |
Definition at line 726 of file fe_subdivision_2D.C.
◆ shape() [105/109]
|
inherited |
Definition at line 744 of file fe_lagrange_vec.C.
◆ shape() [106/109]
|
inherited |
Definition at line 766 of file fe_lagrange_vec.C.
◆ shape() [107/109]
|
inherited |
Definition at line 830 of file fe_lagrange_vec.C.
◆ shape() [108/109]
|
inherited |
Definition at line 1802 of file fe_clough_shape_2D.C.
◆ shape() [109/109]
|
inherited |
Definition at line 1814 of file fe_clough_shape_2D.C.
◆ shape_deriv() [1/109]
|
inherited |
Definition at line 47 of file fe_scalar_shape_3D.C.
◆ shape_deriv() [2/109]
|
inherited |
Definition at line 47 of file fe_scalar_shape_0D.C.
◆ shape_deriv() [3/109]
|
inherited |
Definition at line 47 of file fe_scalar_shape_1D.C.
◆ shape_deriv() [4/109]
|
inherited |
Definition at line 48 of file fe_scalar_shape_2D.C.
◆ shape_deriv() [5/109]
|
inherited |
Definition at line 55 of file fe_szabab_shape_3D.C.
◆ shape_deriv() [6/109]
|
inherited |
Definition at line 56 of file fe_hermite_shape_0D.C.
◆ shape_deriv() [7/109]
|
inherited |
Definition at line 56 of file fe_hierarchic_shape_0D.C.
◆ shape_deriv() [8/109]
|
inherited |
Definition at line 56 of file fe_l2_hierarchic_shape_0D.C.
◆ shape_deriv() [9/109]
|
inherited |
Definition at line 56 of file fe_l2_lagrange_shape_0D.C.
◆ shape_deriv() [10/109]
|
inherited |
Definition at line 56 of file fe_lagrange_shape_0D.C.
◆ shape_deriv() [11/109]
|
inherited |
Definition at line 56 of file fe_monomial_shape_0D.C.
◆ shape_deriv() [12/109]
|
inherited |
Definition at line 56 of file fe_szabab_shape_0D.C.
◆ shape_deriv() [13/109]
|
inherited |
Definition at line 56 of file fe_xyz_shape_0D.C.
◆ shape_deriv() [14/109]
|
inherited |
Definition at line 56 of file fe_bernstein_shape_0D.C.
◆ shape_deriv() [15/109]
|
inherited |
Definition at line 56 of file fe_clough_shape_0D.C.
◆ shape_deriv() [16/109]
|
inherited |
Definition at line 57 of file fe_scalar_shape_0D.C.
◆ shape_deriv() [17/109]
|
inherited |
Definition at line 57 of file fe_scalar_shape_3D.C.
◆ shape_deriv() [18/109]
|
inherited |
Definition at line 57 of file fe_scalar_shape_1D.C.
◆ shape_deriv() [19/109]
|
inherited |
Definition at line 58 of file fe_scalar_shape_2D.C.
◆ shape_deriv() [20/109]
|
inherited |
Definition at line 59 of file fe_clough_shape_3D.C.
◆ shape_deriv() [21/109]
|
inherited |
Definition at line 68 of file fe_szabab_shape_3D.C.
◆ shape_deriv() [22/109]
|
inherited |
Definition at line 69 of file fe_hierarchic_shape_0D.C.
◆ shape_deriv() [23/109]
|
inherited |
Definition at line 69 of file fe_l2_lagrange_shape_0D.C.
◆ shape_deriv() [24/109]
|
inherited |
Definition at line 69 of file fe_l2_hierarchic_shape_0D.C.
◆ shape_deriv() [25/109]
|
inherited |
Definition at line 69 of file fe_monomial_shape_0D.C.
◆ shape_deriv() [26/109]
|
inherited |
Definition at line 69 of file fe_szabab_shape_0D.C.
◆ shape_deriv() [27/109]
|
inherited |
Definition at line 69 of file fe_lagrange_shape_0D.C.
◆ shape_deriv() [28/109]
|
inherited |
Definition at line 69 of file fe_xyz_shape_0D.C.
◆ shape_deriv() [29/109]
|
inherited |
Definition at line 69 of file fe_hermite_shape_0D.C.
◆ shape_deriv() [30/109]
|
inherited |
Definition at line 69 of file fe_clough_shape_0D.C.
◆ shape_deriv() [31/109]
|
inherited |
Definition at line 69 of file fe_bernstein_shape_0D.C.
◆ shape_deriv() [32/109]
|
inherited |
Definition at line 72 of file fe_clough_shape_3D.C.
◆ shape_deriv() [33/109]
|
inherited |
Definition at line 83 of file fe_monomial_shape_1D.C.
◆ shape_deriv() [34/109]
|
inherited |
Definition at line 92 of file fe_szabab_shape_1D.C.
◆ shape_deriv() [35/109]
|
inherited |
Definition at line 93 of file fe_xyz_shape_1D.C.
◆ shape_deriv() [36/109]
|
inherited |
Definition at line 106 of file fe_xyz_shape_1D.C.
◆ shape_deriv() [37/109]
|
inherited |
Definition at line 114 of file fe_hierarchic_shape_1D.C.
◆ shape_deriv() [38/109]
|
inherited |
Definition at line 114 of file fe_l2_hierarchic_shape_1D.C.
◆ shape_deriv() [39/109]
|
inherited |
Definition at line 126 of file fe_monomial_shape_1D.C.
◆ shape_deriv() [40/109]
|
inherited |
Definition at line 130 of file fe_l2_lagrange_shape_1D.C.
◆ shape_deriv() [41/109]
|
inherited |
Definition at line 130 of file fe_lagrange_shape_1D.C.
◆ shape_deriv() [42/109]
|
inherited |
Definition at line 132 of file fe_monomial_shape_2D.C.
◆ shape_deriv() [43/109]
|
staticinherited |
- Returns
- The
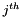 derivative of the
derivative of the 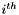 shape function at point
shape function at point p. This method allows you to specify the dimension, element type, and order directly.
On a p-refined element, o should be the total order of the element.
◆ shape_deriv() [44/109]
|
inherited |
Definition at line 138 of file fe_szabab_shape_1D.C.
◆ shape_deriv() [45/109]
|
staticinherited |
- Returns
- The
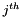 derivative of the
derivative of the 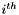 shape function. You must specify element type, and order directly.
shape function. You must specify element type, and order directly.
On a p-refined element, o should be the base order of the element.
◆ shape_deriv() [46/109]
|
inherited |
Definition at line 152 of file fe_xyz_shape_2D.C.
◆ shape_deriv() [47/109]
|
inherited |
Definition at line 165 of file fe_nedelec_one_shape_2D.C.
◆ shape_deriv() [48/109]
|
inherited |
Definition at line 165 of file fe_xyz_shape_2D.C.
◆ shape_deriv() [49/109]
|
inherited |
Definition at line 178 of file fe_nedelec_one_shape_2D.C.
◆ shape_deriv() [50/109]
|
inherited |
Definition at line 185 of file fe_hierarchic_shape_1D.C.
◆ shape_deriv() [51/109]
|
inherited |
Definition at line 185 of file fe_l2_hierarchic_shape_1D.C.
◆ shape_deriv() [52/109]
|
inherited |
Definition at line 194 of file fe_nedelec_one_shape_3D.C.
◆ shape_deriv() [53/109]
|
inherited |
Definition at line 200 of file fe_monomial_shape_3D.C.
◆ shape_deriv() [54/109]
|
inherited |
Definition at line 203 of file fe_bernstein_shape_1D.C.
◆ shape_deriv() [55/109]
|
inherited |
Definition at line 205 of file fe_nedelec_one_shape_3D.C.
◆ shape_deriv() [56/109]
|
inherited |
Definition at line 219 of file fe_l2_lagrange_shape_1D.C.
◆ shape_deriv() [57/109]
|
inherited |
Definition at line 219 of file fe_lagrange_shape_1D.C.
◆ shape_deriv() [58/109]
|
inherited |
Definition at line 222 of file fe_l2_lagrange_shape_2D.C.
◆ shape_deriv() [59/109]
|
inherited |
Definition at line 222 of file fe_xyz_shape_3D.C.
◆ shape_deriv() [60/109]
|
inherited |
Definition at line 224 of file fe_lagrange_shape_2D.C.
◆ shape_deriv() [61/109]
|
inherited |
Definition at line 231 of file fe_hierarchic_shape_2D.C.
◆ shape_deriv() [62/109]
|
inherited |
Definition at line 231 of file fe_l2_hierarchic_shape_2D.C.
◆ shape_deriv() [63/109]
|
inherited |
Definition at line 235 of file fe_xyz_shape_3D.C.
◆ shape_deriv() [64/109]
|
inherited |
Definition at line 237 of file fe_hermite_shape_1D.C.
◆ shape_deriv() [65/109]
|
inherited |
Definition at line 244 of file fe_l2_hierarchic_shape_2D.C.
◆ shape_deriv() [66/109]
|
inherited |
Definition at line 244 of file fe_hierarchic_shape_2D.C.
◆ shape_deriv() [67/109]
|
inherited |
Definition at line 250 of file fe_hermite_shape_1D.C.
◆ shape_deriv() [68/109]
|
inherited |
Definition at line 251 of file fe_hermite_shape_2D.C.
◆ shape_deriv() [69/109]
|
inherited |
Definition at line 264 of file fe_hermite_shape_2D.C.
◆ shape_deriv() [70/109]
|
inherited |
Definition at line 276 of file fe_clough_shape_1D.C.
◆ shape_deriv() [71/109]
|
inherited |
Definition at line 289 of file fe_clough_shape_1D.C.
◆ shape_deriv() [72/109]
|
inherited |
Definition at line 304 of file fe_monomial_shape_2D.C.
◆ shape_deriv() [73/109]
|
inherited |
Definition at line 361 of file fe_bernstein_shape_1D.C.
◆ shape_deriv() [74/109]
|
inherited |
Definition at line 371 of file fe_l2_lagrange_shape_3D.C.
◆ shape_deriv() [75/109]
|
inherited |
Definition at line 386 of file fe_bernstein_shape_2D.C.
◆ shape_deriv() [76/109]
|
inherited |
Definition at line 399 of file fe_bernstein_shape_2D.C.
◆ shape_deriv() [77/109]
|
inherited |
Definition at line 447 of file fe_hermite_shape_3D.C.
◆ shape_deriv() [78/109]
|
inherited |
Definition at line 460 of file fe_hermite_shape_3D.C.
◆ shape_deriv() [79/109]
|
inherited |
Definition at line 544 of file fe_lagrange_vec.C.
◆ shape_deriv() [80/109]
|
inherited |
Definition at line 550 of file fe_l2_lagrange_shape_2D.C.
◆ shape_deriv() [81/109]
|
inherited |
Definition at line 552 of file fe_lagrange_shape_2D.C.
◆ shape_deriv() [82/109]
|
inherited |
◆ shape_deriv() [83/109]
|
inherited |
Definition at line 566 of file fe_lagrange_vec.C.
◆ shape_deriv() [84/109]
|
inherited |
Definition at line 573 of file fe_lagrange_shape_3D.C.
◆ shape_deriv() [85/109]
|
inherited |
Definition at line 599 of file fe_nedelec_one.C.
◆ shape_deriv() [86/109]
|
inherited |
Definition at line 602 of file fe_lagrange_vec.C.
◆ shape_deriv() [87/109]
|
inherited |
Definition at line 603 of file fe_nedelec_one.C.
◆ shape_deriv() [88/109]
|
inherited |
Definition at line 622 of file fe_nedelec_one.C.
◆ shape_deriv() [89/109]
|
inherited |
Definition at line 626 of file fe_nedelec_one.C.
◆ shape_deriv() [90/109]
|
inherited |
Definition at line 638 of file fe_monomial_shape_3D.C.
◆ shape_deriv() [91/109]
|
inherited |
Definition at line 670 of file fe_lagrange_vec.C.
◆ shape_deriv() [92/109]
|
inherited |
Definition at line 704 of file fe_l2_hierarchic_shape_3D.C.
◆ shape_deriv() [93/109]
|
inherited |
Definition at line 704 of file fe_hierarchic_shape_3D.C.
◆ shape_deriv() [94/109]
|
inherited |
Definition at line 717 of file fe_l2_hierarchic_shape_3D.C.
◆ shape_deriv() [95/109]
|
inherited |
Definition at line 717 of file fe_hierarchic_shape_3D.C.
◆ shape_deriv() [96/109]
|
inherited |
Definition at line 728 of file fe_lagrange_vec.C.
◆ shape_deriv() [97/109]
|
inherited |
Definition at line 737 of file fe_szabab_shape_2D.C.
◆ shape_deriv() [98/109]
|
inherited |
Definition at line 738 of file fe_subdivision_2D.C.
◆ shape_deriv() [99/109]
|
inherited |
Definition at line 750 of file fe_szabab_shape_2D.C.
◆ shape_deriv() [100/109]
|
inherited |
Definition at line 750 of file fe_lagrange_vec.C.
◆ shape_deriv() [101/109]
|
inherited |
Definition at line 765 of file fe_subdivision_2D.C.
◆ shape_deriv() [102/109]
|
inherited |
Definition at line 786 of file fe_lagrange_vec.C.
◆ shape_deriv() [103/109]
|
inherited |
Definition at line 853 of file fe_lagrange_vec.C.
◆ shape_deriv() [104/109]
|
inherited |
Definition at line 1195 of file fe_l2_lagrange_shape_3D.C.
◆ shape_deriv() [105/109]
|
inherited |
Definition at line 1382 of file fe_bernstein_shape_3D.C.
◆ shape_deriv() [106/109]
|
inherited |
Definition at line 1395 of file fe_bernstein_shape_3D.C.
◆ shape_deriv() [107/109]
|
inherited |
Definition at line 1914 of file fe_lagrange_shape_3D.C.
◆ shape_deriv() [108/109]
|
inherited |
Definition at line 1994 of file fe_clough_shape_2D.C.
◆ shape_deriv() [109/109]
|
inherited |
Definition at line 2007 of file fe_clough_shape_2D.C.
◆ shape_second_deriv() [1/103]
|
inherited |
Definition at line 67 of file fe_scalar_shape_3D.C.
◆ shape_second_deriv() [2/103]
|
inherited |
Definition at line 67 of file fe_scalar_shape_1D.C.
◆ shape_second_deriv() [3/103]
|
inherited |
Definition at line 67 of file fe_scalar_shape_0D.C.
◆ shape_second_deriv() [4/103]
|
inherited |
Definition at line 69 of file fe_scalar_shape_2D.C.
◆ shape_second_deriv() [5/103]
|
inherited |
Definition at line 77 of file fe_scalar_shape_1D.C.
◆ shape_second_deriv() [6/103]
|
inherited |
Definition at line 77 of file fe_scalar_shape_0D.C.
◆ shape_second_deriv() [7/103]
|
inherited |
Definition at line 77 of file fe_scalar_shape_3D.C.
◆ shape_second_deriv() [8/103]
|
inherited |
Definition at line 79 of file fe_scalar_shape_2D.C.
◆ shape_second_deriv() [9/103]
|
inherited |
Definition at line 81 of file fe_szabab_shape_3D.C.
◆ shape_second_deriv() [10/103]
|
inherited |
Definition at line 83 of file fe_bernstein_shape_0D.C.
◆ shape_second_deriv() [11/103]
|
inherited |
Definition at line 83 of file fe_lagrange_shape_0D.C.
◆ shape_second_deriv() [12/103]
|
inherited |
Definition at line 83 of file fe_szabab_shape_0D.C.
◆ shape_second_deriv() [13/103]
|
inherited |
Definition at line 83 of file fe_xyz_shape_0D.C.
◆ shape_second_deriv() [14/103]
|
inherited |
Definition at line 83 of file fe_monomial_shape_0D.C.
◆ shape_second_deriv() [15/103]
|
inherited |
Definition at line 83 of file fe_l2_hierarchic_shape_0D.C.
◆ shape_second_deriv() [16/103]
|
inherited |
Definition at line 83 of file fe_clough_shape_0D.C.
◆ shape_second_deriv() [17/103]
|
inherited |
Definition at line 83 of file fe_l2_lagrange_shape_0D.C.
◆ shape_second_deriv() [18/103]
|
inherited |
Definition at line 83 of file fe_hermite_shape_0D.C.
◆ shape_second_deriv() [19/103]
|
inherited |
Definition at line 83 of file fe_hierarchic_shape_0D.C.
◆ shape_second_deriv() [20/103]
|
inherited |
Definition at line 86 of file fe_clough_shape_3D.C.
◆ shape_second_deriv() [21/103]
|
inherited |
Definition at line 94 of file fe_szabab_shape_3D.C.
◆ shape_second_deriv() [22/103]
|
inherited |
Definition at line 96 of file fe_l2_lagrange_shape_0D.C.
◆ shape_second_deriv() [23/103]
|
inherited |
Definition at line 96 of file fe_hierarchic_shape_0D.C.
◆ shape_second_deriv() [24/103]
|
inherited |
Definition at line 96 of file fe_monomial_shape_0D.C.
◆ shape_second_deriv() [25/103]
|
inherited |
Definition at line 96 of file fe_xyz_shape_0D.C.
◆ shape_second_deriv() [26/103]
|
inherited |
Definition at line 96 of file fe_szabab_shape_0D.C.
◆ shape_second_deriv() [27/103]
|
inherited |
Definition at line 96 of file fe_lagrange_shape_0D.C.
◆ shape_second_deriv() [28/103]
|
inherited |
Definition at line 96 of file fe_bernstein_shape_0D.C.
◆ shape_second_deriv() [29/103]
|
inherited |
Definition at line 96 of file fe_l2_hierarchic_shape_0D.C.
◆ shape_second_deriv() [30/103]
|
inherited |
Definition at line 96 of file fe_clough_shape_0D.C.
◆ shape_second_deriv() [31/103]
|
inherited |
Definition at line 96 of file fe_hermite_shape_0D.C.
◆ shape_second_deriv() [32/103]
|
inherited |
Definition at line 141 of file fe_monomial_shape_1D.C.
◆ shape_second_deriv() [33/103]
|
inherited |
Definition at line 153 of file fe_szabab_shape_1D.C.
◆ shape_second_deriv() [34/103]
|
inherited |
Definition at line 160 of file fe_xyz_shape_1D.C.
◆ shape_second_deriv() [35/103]
|
inherited |
Definition at line 173 of file fe_xyz_shape_1D.C.
◆ shape_second_deriv() [36/103]
|
inherited |
Definition at line 173 of file fe_szabab_shape_1D.C.
◆ shape_second_deriv() [37/103]
|
staticinherited |
- Returns
- The second
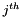 derivative of the
derivative of the 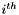 shape function at the point
shape function at the point p.
- Note
- Cross-derivatives are indexed according to: j = 0 ==> d^2 phi / dxi^2 j = 1 ==> d^2 phi / dxi deta j = 2 ==> d^2 phi / deta^2 j = 3 ==> d^2 phi / dxi dzeta j = 4 ==> d^2 phi / deta dzeta j = 5 ==> d^2 phi / dzeta^2
-
Computing second derivatives is not currently supported for all element types:
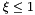 (Clough, Hermite and Subdivision), Lagrange, Hierarchic, L2_Hierarchic, and Monomial are supported. All other element types return an error when asked for second derivatives.
(Clough, Hermite and Subdivision), Lagrange, Hierarchic, L2_Hierarchic, and Monomial are supported. All other element types return an error when asked for second derivatives.
On a p-refined element, o should be the total order of the element.
◆ shape_second_deriv() [38/103]
|
inherited |
Definition at line 181 of file fe_monomial_shape_1D.C.
◆ shape_second_deriv() [39/103]
|
staticinherited |
- Returns
- The second
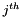 derivative of the
derivative of the 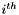 shape function at the point
shape function at the point p.
- Note
- Cross-derivatives are indexed according to: j = 0 ==> d^2 phi / dxi^2 j = 1 ==> d^2 phi / dxi deta j = 2 ==> d^2 phi / deta^2 j = 3 ==> d^2 phi / dxi dzeta j = 4 ==> d^2 phi / deta dzeta j = 5 ==> d^2 phi / dzeta^2
-
Computing second derivatives is not currently supported for all element types:
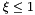 (Clough, Hermite and Subdivision), Lagrange, Hierarchic, L2_Hierarchic, and Monomial are supported. All other element types return an error when asked for second derivatives.
(Clough, Hermite and Subdivision), Lagrange, Hierarchic, L2_Hierarchic, and Monomial are supported. All other element types return an error when asked for second derivatives.
On a p-refined element, o should be the base order of the element.
◆ shape_second_deriv() [40/103]
|
inherited |
Definition at line 200 of file fe_l2_hierarchic_shape_1D.C.
◆ shape_second_deriv() [41/103]
|
inherited |
Definition at line 200 of file fe_hierarchic_shape_1D.C.
◆ shape_second_deriv() [42/103]
|
inherited |
Definition at line 235 of file fe_l2_lagrange_shape_1D.C.
◆ shape_second_deriv() [43/103]
|
inherited |
Definition at line 235 of file fe_lagrange_shape_1D.C.
◆ shape_second_deriv() [44/103]
|
inherited |
Definition at line 268 of file fe_hierarchic_shape_1D.C.
◆ shape_second_deriv() [45/103]
|
inherited |
Definition at line 268 of file fe_l2_hierarchic_shape_1D.C.
◆ shape_second_deriv() [46/103]
|
inherited |
Definition at line 301 of file fe_hermite_shape_1D.C.
◆ shape_second_deriv() [47/103]
|
inherited |
Definition at line 305 of file fe_lagrange_shape_1D.C.
◆ shape_second_deriv() [48/103]
|
inherited |
Definition at line 305 of file fe_l2_lagrange_shape_1D.C.
◆ shape_second_deriv() [49/103]
|
inherited |
Definition at line 319 of file fe_monomial_shape_2D.C.
◆ shape_second_deriv() [50/103]
|
inherited |
Definition at line 327 of file fe_hermite_shape_2D.C.
◆ shape_second_deriv() [51/103]
|
inherited |
Definition at line 330 of file fe_nedelec_one_shape_2D.C.
◆ shape_second_deriv() [52/103]
|
inherited |
Definition at line 341 of file fe_clough_shape_1D.C.
◆ shape_second_deriv() [53/103]
|
inherited |
Definition at line 343 of file fe_nedelec_one_shape_2D.C.
◆ shape_second_deriv() [54/103]
|
inherited |
Definition at line 356 of file fe_xyz_shape_2D.C.
◆ shape_second_deriv() [55/103]
|
inherited |
Definition at line 369 of file fe_xyz_shape_2D.C.
◆ shape_second_deriv() [56/103]
|
inherited |
Definition at line 376 of file fe_bernstein_shape_1D.C.
◆ shape_second_deriv() [57/103]
|
inherited |
Definition at line 383 of file fe_hierarchic_shape_2D.C.
◆ shape_second_deriv() [58/103]
|
inherited |
Definition at line 384 of file fe_l2_hierarchic_shape_2D.C.
◆ shape_second_deriv() [59/103]
|
inherited |
Definition at line 396 of file fe_hierarchic_shape_2D.C.
◆ shape_second_deriv() [60/103]
|
inherited |
Definition at line 397 of file fe_bernstein_shape_1D.C.
◆ shape_second_deriv() [61/103]
|
inherited |
Definition at line 397 of file fe_l2_hierarchic_shape_2D.C.
◆ shape_second_deriv() [62/103]
|
inherited |
Definition at line 491 of file fe_nedelec_one_shape_3D.C.
◆ shape_second_deriv() [63/103]
|
inherited |
Definition at line 504 of file fe_nedelec_one_shape_3D.C.
◆ shape_second_deriv() [64/103]
|
inherited |
Definition at line 538 of file fe_monomial_shape_2D.C.
◆ shape_second_deriv() [65/103]
|
inherited |
Definition at line 541 of file fe_hermite_shape_3D.C.
◆ shape_second_deriv() [66/103]
|
inherited |
Definition at line 551 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [67/103]
|
inherited |
Definition at line 563 of file fe_bernstein_shape_2D.C.
◆ shape_second_deriv() [68/103]
|
inherited |
◆ shape_second_deriv() [69/103]
|
inherited |
Definition at line 567 of file fe_l2_lagrange_shape_2D.C.
◆ shape_second_deriv() [70/103]
|
inherited |
Definition at line 569 of file fe_lagrange_shape_2D.C.
◆ shape_second_deriv() [71/103]
|
inherited |
Definition at line 573 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [72/103]
|
inherited |
Definition at line 583 of file fe_bernstein_shape_2D.C.
◆ shape_second_deriv() [73/103]
|
inherited |
Definition at line 607 of file fe_nedelec_one.C.
◆ shape_second_deriv() [74/103]
|
inherited |
Definition at line 611 of file fe_nedelec_one.C.
◆ shape_second_deriv() [75/103]
|
inherited |
Definition at line 623 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [76/103]
|
inherited |
Definition at line 630 of file fe_nedelec_one.C.
◆ shape_second_deriv() [77/103]
|
inherited |
Definition at line 634 of file fe_nedelec_one.C.
◆ shape_second_deriv() [78/103]
|
inherited |
Definition at line 653 of file fe_monomial_shape_3D.C.
◆ shape_second_deriv() [79/103]
|
inherited |
Definition at line 694 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [80/103]
|
inherited |
Definition at line 696 of file fe_xyz_shape_3D.C.
◆ shape_second_deriv() [81/103]
|
inherited |
Definition at line 709 of file fe_xyz_shape_3D.C.
◆ shape_second_deriv() [82/103]
|
inherited |
Definition at line 735 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [83/103]
|
inherited |
Definition at line 757 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [84/103]
|
inherited |
Definition at line 770 of file fe_l2_hierarchic_shape_3D.C.
◆ shape_second_deriv() [85/103]
|
inherited |
Definition at line 770 of file fe_hierarchic_shape_3D.C.
◆ shape_second_deriv() [86/103]
|
inherited |
Definition at line 778 of file fe_subdivision_2D.C.
◆ shape_second_deriv() [87/103]
|
inherited |
Definition at line 783 of file fe_hierarchic_shape_3D.C.
◆ shape_second_deriv() [88/103]
|
inherited |
Definition at line 783 of file fe_l2_hierarchic_shape_3D.C.
◆ shape_second_deriv() [89/103]
|
inherited |
Definition at line 805 of file fe_subdivision_2D.C.
◆ shape_second_deriv() [90/103]
|
inherited |
Definition at line 807 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [91/103]
|
inherited |
Definition at line 877 of file fe_lagrange_vec.C.
◆ shape_second_deriv() [92/103]
|
inherited |
Definition at line 904 of file fe_l2_lagrange_shape_2D.C.
◆ shape_second_deriv() [93/103]
|
inherited |
Definition at line 908 of file fe_lagrange_shape_2D.C.
◆ shape_second_deriv() [94/103]
|
inherited |
Definition at line 1210 of file fe_l2_lagrange_shape_3D.C.
◆ shape_second_deriv() [95/103]
|
inherited |
Definition at line 1301 of file fe_monomial_shape_3D.C.
◆ shape_second_deriv() [96/103]
|
inherited |
Definition at line 1400 of file fe_szabab_shape_2D.C.
◆ shape_second_deriv() [97/103]
|
inherited |
Definition at line 1420 of file fe_szabab_shape_2D.C.
◆ shape_second_deriv() [98/103]
|
inherited |
Definition at line 1448 of file fe_l2_lagrange_shape_3D.C.
◆ shape_second_deriv() [99/103]
|
inherited |
Definition at line 1929 of file fe_lagrange_shape_3D.C.
◆ shape_second_deriv() [100/103]
|
inherited |
Definition at line 2188 of file fe_clough_shape_2D.C.
◆ shape_second_deriv() [101/103]
|
inherited |
Definition at line 2965 of file fe_bernstein_shape_3D.C.
◆ shape_second_deriv() [102/103]
|
inherited |
Definition at line 2985 of file fe_bernstein_shape_3D.C.
◆ shape_second_deriv() [103/103]
|
inherited |
Definition at line 3645 of file fe_lagrange_shape_3D.C.
◆ shapes_need_reinit() [1/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 137 of file fe_scalar.C.
◆ shapes_need_reinit() [2/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 138 of file fe_scalar.C.
◆ shapes_need_reinit() [3/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 139 of file fe_scalar.C.
◆ shapes_need_reinit() [4/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 140 of file fe_scalar.C.
◆ shapes_need_reinit() [5/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 222 of file fe_l2_hierarchic.C.
◆ shapes_need_reinit() [6/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 223 of file fe_l2_hierarchic.C.
◆ shapes_need_reinit() [7/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 224 of file fe_l2_hierarchic.C.
◆ shapes_need_reinit() [8/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 225 of file fe_l2_hierarchic.C.
◆ shapes_need_reinit() [9/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 319 of file fe_clough.C.
◆ shapes_need_reinit() [10/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 320 of file fe_clough.C.
◆ shapes_need_reinit() [11/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 321 of file fe_clough.C.
◆ shapes_need_reinit() [12/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 322 of file fe_clough.C.
◆ shapes_need_reinit() [13/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 370 of file fe_hermite.C.
◆ shapes_need_reinit() [14/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 371 of file fe_hermite.C.
◆ shapes_need_reinit() [15/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 372 of file fe_hermite.C.
◆ shapes_need_reinit() [16/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 373 of file fe_hermite.C.
◆ shapes_need_reinit() [17/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 398 of file fe_hierarchic.C.
◆ shapes_need_reinit() [18/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 399 of file fe_hierarchic.C.
◆ shapes_need_reinit() [19/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 400 of file fe_hierarchic.C.
◆ shapes_need_reinit() [20/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 401 of file fe_hierarchic.C.
◆ shapes_need_reinit() [21/54]
|
overridevirtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
◆ shapes_need_reinit() [22/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 425 of file fe_monomial.C.
◆ shapes_need_reinit() [23/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 426 of file fe_monomial.C.
◆ shapes_need_reinit() [24/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 427 of file fe_monomial.C.
◆ shapes_need_reinit() [25/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 428 of file fe_monomial.C.
◆ shapes_need_reinit() [26/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 466 of file fe_bernstein.C.
◆ shapes_need_reinit() [27/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 467 of file fe_bernstein.C.
◆ shapes_need_reinit() [28/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 468 of file fe_bernstein.C.
◆ shapes_need_reinit() [29/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 469 of file fe_bernstein.C.
◆ shapes_need_reinit() [30/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 486 of file fe_l2_lagrange.C.
◆ shapes_need_reinit() [31/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 487 of file fe_l2_lagrange.C.
◆ shapes_need_reinit() [32/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 488 of file fe_l2_lagrange.C.
◆ shapes_need_reinit() [33/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 489 of file fe_l2_lagrange.C.
◆ shapes_need_reinit() [34/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 556 of file fe_nedelec_one.C.
◆ shapes_need_reinit() [35/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 557 of file fe_nedelec_one.C.
◆ shapes_need_reinit() [36/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 558 of file fe_nedelec_one.C.
◆ shapes_need_reinit() [37/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 559 of file fe_nedelec_one.C.
◆ shapes_need_reinit() [38/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 889 of file fe_lagrange.C.
◆ shapes_need_reinit() [39/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 890 of file fe_lagrange.C.
◆ shapes_need_reinit() [40/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 891 of file fe_lagrange.C.
◆ shapes_need_reinit() [41/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 892 of file fe_lagrange.C.
◆ shapes_need_reinit() [42/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 916 of file fe_subdivision_2D.C.
◆ shapes_need_reinit() [43/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 939 of file fe_lagrange_vec.C.
◆ shapes_need_reinit() [44/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 940 of file fe_lagrange_vec.C.
◆ shapes_need_reinit() [45/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 941 of file fe_lagrange_vec.C.
◆ shapes_need_reinit() [46/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 942 of file fe_lagrange_vec.C.
◆ shapes_need_reinit() [47/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
◆ shapes_need_reinit() [48/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
◆ shapes_need_reinit() [49/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
◆ shapes_need_reinit() [50/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
◆ shapes_need_reinit() [51/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 1303 of file fe_szabab.C.
◆ shapes_need_reinit() [52/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 1304 of file fe_szabab.C.
◆ shapes_need_reinit() [53/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 1305 of file fe_szabab.C.
◆ shapes_need_reinit() [54/54]
|
virtualinherited |
- Returns
truewhen the shape functions (for thisFEFamily) depend on the particular element, and therefore needs to be re-initialized for each new element.falseotherwise.
Implements libMesh::FEAbstract.
Definition at line 1306 of file fe_szabab.C.
◆ side_map() [1/2]
|
overridevirtualinherited |
Computes the reference space quadrature points on the side of an element based on the side quadrature points.
Implements libMesh::FEAbstract.
Definition at line 353 of file fe_boundary.C.
◆ side_map() [2/2]
|
virtualinherited |
Computes the reference space quadrature points on the side of an element based on the side quadrature points.
Implements libMesh::FEAbstract.
Definition at line 856 of file fe_subdivision_2D.C.
Member Data Documentation
◆ _counts
|
staticprotectedinherited |
Actually holds the data.
Definition at line 122 of file reference_counter.h.
Referenced by libMesh::ReferenceCounter::get_info(), libMesh::ReferenceCounter::increment_constructor_count(), and libMesh::ReferenceCounter::increment_destructor_count().
◆ _enable_print_counter
|
staticprotectedinherited |
Flag to control whether reference count information is printed when print_info is called.
Definition at line 141 of file reference_counter.h.
Referenced by libMesh::ReferenceCounter::disable_print_counter_info(), libMesh::ReferenceCounter::enable_print_counter_info(), and libMesh::ReferenceCounter::print_info().
◆ _fe_map
|
protectedinherited |
Definition at line 525 of file fe_abstract.h.
Referenced by libMesh::FEAbstract::get_curvatures(), libMesh::FEAbstract::get_d2xyzdeta2(), libMesh::FEAbstract::get_d2xyzdetadzeta(), libMesh::FEAbstract::get_d2xyzdxi2(), libMesh::FEAbstract::get_d2xyzdxideta(), libMesh::FEAbstract::get_d2xyzdxidzeta(), libMesh::FEAbstract::get_d2xyzdzeta2(), libMesh::FEAbstract::get_detadx(), libMesh::FEAbstract::get_detady(), libMesh::FEAbstract::get_detadz(), libMesh::FEAbstract::get_dxidx(), libMesh::FEAbstract::get_dxidy(), libMesh::FEAbstract::get_dxidz(), libMesh::FEAbstract::get_dxyzdeta(), libMesh::FEAbstract::get_dxyzdxi(), libMesh::FEAbstract::get_dxyzdzeta(), libMesh::FEAbstract::get_dzetadx(), libMesh::FEAbstract::get_dzetady(), libMesh::FEAbstract::get_dzetadz(), libMesh::FEAbstract::get_fe_map(), libMesh::FEAbstract::get_JxW(), libMesh::FEAbstract::get_normals(), libMesh::FEAbstract::get_tangents(), libMesh::FEAbstract::get_xyz(), init_shape_functions(), libMesh::FEAbstract::print_JxW(), and libMesh::FEAbstract::print_xyz().
◆ _fe_trans
|
protectedinherited |
◆ _mutex
|
staticprotectedinherited |
Mutual exclusion object to enable thread-safe reference counting.
Definition at line 135 of file reference_counter.h.
◆ _n_objects
|
staticprotectedinherited |
The number of objects. Print the reference count information when the number returns to 0.
Definition at line 130 of file reference_counter.h.
Referenced by libMesh::ReferenceCounter::n_objects(), libMesh::ReferenceCounter::ReferenceCounter(), and libMesh::ReferenceCounter::~ReferenceCounter().
◆ _p_level
|
protectedinherited |
The p refinement level the current data structures are set up for.
Definition at line 587 of file fe_abstract.h.
Referenced by libMesh::FEAbstract::get_order(), and libMesh::FEAbstract::get_p_level().
◆ cached_nodes
|
protectedinherited |
◆ calculate_curl_phi
|
mutableprotectedinherited |
Should we calculate shape function curls?
Definition at line 557 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi().
◆ calculate_d2phi
|
mutableprotectedinherited |
Should we calculate shape function hessians?
Definition at line 552 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2(), and libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2().
◆ calculate_div_phi
|
mutableprotectedinherited |
Should we calculate shape function divergences?
Definition at line 562 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi().
◆ calculate_dphi
|
mutableprotectedinherited |
Should we calculate shape function gradients?
Definition at line 547 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy(), and libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz().
◆ calculate_dphiref
|
mutableprotectedinherited |
Should we calculate reference shape function gradients?
Definition at line 567 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidxi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz(), and libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidzeta().
◆ calculate_phi
|
mutableprotectedinherited |
Should we calculate shape functions?
Definition at line 542 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_phi().
◆ calculations_started
|
mutableprotectedinherited |
Have calculations with this object already been started? Then all get_* functions should already have been called.
Definition at line 537 of file fe_abstract.h.
Referenced by libMesh::FEGenericBase< FEOutputType< T >::type >::get_curl_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phideta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidetadzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidx2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxdz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxi2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidxidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidy2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidydz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidz2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_d2phidzeta2(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_div_phi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphideta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidx(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidxi(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidy(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidz(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_dphidzeta(), libMesh::FEGenericBase< FEOutputType< T >::type >::get_phi(), and init_shape_functions().
◆ curl_phi
|
protectedinherited |
◆ d2phi
|
protectedinherited |
Shape function second derivative values.
Definition at line 551 of file fe_base.h.
Referenced by init_shape_functions().
◆ d2phideta2
|
protectedinherited |
Shape function second derivatives in the eta direction.
Definition at line 571 of file fe_base.h.
Referenced by init_shape_functions().
◆ d2phidetadzeta
|
protectedinherited |
◆ d2phidx2
|
protectedinherited |
◆ d2phidxdy
|
protectedinherited |
◆ d2phidxdz
|
protectedinherited |
◆ d2phidxi2
|
protectedinherited |
Shape function second derivatives in the xi direction.
Definition at line 556 of file fe_base.h.
Referenced by init_shape_functions().
◆ d2phidxideta
|
protectedinherited |
Shape function second derivatives in the xi-eta direction.
Definition at line 561 of file fe_base.h.
Referenced by init_shape_functions().
◆ d2phidxidzeta
|
protectedinherited |
◆ d2phidy2
|
protectedinherited |
◆ d2phidydz
|
protectedinherited |
◆ d2phidz2
|
protectedinherited |
◆ d2phidzeta2
|
protectedinherited |
◆ dim
|
protectedinherited |
The dimensionality of the object
Definition at line 531 of file fe_abstract.h.
Referenced by libMesh::FEAbstract::build(), and libMesh::FEAbstract::get_dim().
◆ div_phi
|
protectedinherited |
◆ dphase
|
protectedinherited |
◆ dphi
|
protectedinherited |
Shape function derivative values.
Definition at line 503 of file fe_base.h.
Referenced by init_shape_functions().
◆ dphideta
|
protectedinherited |
Shape function derivatives in the eta direction.
Definition at line 523 of file fe_base.h.
Referenced by init_shape_functions().
◆ dphidx
|
protectedinherited |
◆ dphidxi
|
protectedinherited |
Shape function derivatives in the xi direction.
Definition at line 518 of file fe_base.h.
Referenced by init_shape_functions().
◆ dphidy
|
protectedinherited |
◆ dphidz
|
protectedinherited |
◆ dphidzeta
|
protectedinherited |
◆ dweight
|
protectedinherited |
◆ elem_type
|
protectedinherited |
The element type the current data structures are set up for.
Definition at line 581 of file fe_abstract.h.
Referenced by attach_quadrature_rule(), and libMesh::FEAbstract::get_type().
◆ fe_type
|
protectedinherited |
The finite element type for this object.
- Note
- This should be constant for the object.
Definition at line 575 of file fe_abstract.h.
Referenced by libMesh::FEAbstract::compute_node_constraints(), libMesh::FEAbstract::compute_periodic_node_constraints(), libMesh::FEAbstract::get_family(), libMesh::FEAbstract::get_fe_type(), libMesh::FEAbstract::get_order(), libMesh::InfFE< Dim, T_radial, T_map >::InfFE(), init_shape_functions(), and libMesh::FEAbstract::set_fe_order().
◆ last_edge
|
protectedinherited |
◆ last_side
|
protectedinherited |
◆ phi
|
protectedinherited |
Shape function values.
Definition at line 498 of file fe_base.h.
Referenced by init_shape_functions().
◆ qrule
|
protectedinherited |
A pointer to the quadrature rule employed
Definition at line 592 of file fe_abstract.h.
Referenced by attach_quadrature_rule().
◆ shapes_on_quadrature
|
protectedinherited |
A flag indicating if current data structures correspond to quadrature rule points
Definition at line 598 of file fe_abstract.h.
◆ weight
|
protectedinherited |
The documentation for this class was generated from the following files:
generated by

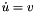 , over all quadrature points.
, over all quadrature points.