Public Member Functions | Static Public Member Functions | List of all members
libMesh::HCurlFETransformation< OutputShape > Class Template Reference

#include <fe_transformation_base.h>

Inheritance diagram for libMesh::HCurlFETransformation< OutputShape >:
Inheritance graph
[legend]

Public Member Functions

 HCurlFETransformation ()
 
virtual ~HCurlFETransformation ()
 
virtual void init_map_phi (const FEGenericBase< OutputShape > &fe) const override
 
virtual void init_map_dphi (const FEGenericBase< OutputShape > &fe) const override
 
virtual void init_map_d2phi (const FEGenericBase< OutputShape > &fe) const override
 
virtual void map_phi (const unsigned int dim, const Elem *const elem, const std::vector< Point > &qp, const FEGenericBase< OutputShape > &fe, std::vector< std::vector< OutputShape >> &phi) const override
 
virtual void map_dphi (const unsigned int, const Elem *const, const std::vector< Point > &, const FEGenericBase< OutputShape > &, std::vector< std::vector< typename FEGenericBase< OutputShape >::OutputGradient >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &) const override
 
virtual void map_d2phi (const unsigned int, const std::vector< Point > &, const FEGenericBase< OutputShape > &, std::vector< std::vector< typename FEGenericBase< OutputShape >::OutputTensor >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &, std::vector< std::vector< OutputShape >> &) const override
 
virtual void map_curl (const unsigned int dim, const Elem *const elem, const std::vector< Point > &qp, const FEGenericBase< OutputShape > &fe, std::vector< std::vector< OutputShape >> &curl_phi) const override
 
virtual void map_div (const unsigned int, const Elem *const, const std::vector< Point > &, const FEGenericBase< OutputShape > &, std::vector< std::vector< typename FEGenericBase< OutputShape >::OutputDivergence >> &) const override
 
template<>
void init_map_phi (const FEGenericBase< Real > &) const
 
template<>
void init_map_dphi (const FEGenericBase< Real > &) const
 
template<>
void init_map_d2phi (const FEGenericBase< Real > &) const
 
template<>
void map_phi (const unsigned int, const Elem *const, const std::vector< Point > &, const FEGenericBase< Real > &, std::vector< std::vector< Real >> &) const
 
template<>
void map_curl (const unsigned int, const Elem *const, const std::vector< Point > &, const FEGenericBase< Real > &, std::vector< std::vector< Real >> &) const
 

Static Public Member Functions

static std::unique_ptr< FETransformationBase< OutputShape > > build (const FEType &type)
 

Detailed Description

template<typename OutputShape>
class libMesh::HCurlFETransformation< OutputShape >

This class handles the computation of the shape functions in the physical domain for HCurl conforming elements. This class assumes the FEGenericBase object has been initialized in the reference domain (i.e. init_shape_functions has been called).

Author
Paul T. Bauman
Date
2012

Definition at line 29 of file fe_transformation_base.h.

Constructor & Destructor Documentation

◆ HCurlFETransformation()

template<typename OutputShape >
libMesh::HCurlFETransformation< OutputShape >::HCurlFETransformation ( )
inline

Definition at line 40 of file hcurl_fe_transformation.h.

41  : FETransformationBase<OutputShape>(){}

◆ ~HCurlFETransformation()

template<typename OutputShape >
virtual libMesh::HCurlFETransformation< OutputShape >::~HCurlFETransformation ( )
inlinevirtual

Definition at line 43 of file hcurl_fe_transformation.h.

43 {}

Member Function Documentation

◆ build()

template<typename OutputShape >
std::unique_ptr< FETransformationBase< OutputShape > > libMesh::FETransformationBase< OutputShape >::build ( const FEType &  type)
staticinherited

Builds an FETransformation object based on the finite element type

Definition at line 28 of file fe_transformation_base.C.

References libMesh::BERNSTEIN, libMesh::CLOUGH, libMesh::FEType::family, libMesh::HERMITE, libMesh::HIERARCHIC, libMesh::JACOBI_20_00, libMesh::JACOBI_30_00, libMesh::L2_HIERARCHIC, libMesh::L2_LAGRANGE, libMesh::LAGRANGE, libMesh::LAGRANGE_VEC, libMesh::MONOMIAL, libMesh::NEDELEC_ONE, libMesh::SCALAR, libMesh::SUBDIVISION, libMesh::SZABAB, and libMesh::XYZ.

29 {
30  switch (fe_type.family)
31  {
32  // H1 Conforming Elements
33  case LAGRANGE:
34  case HIERARCHIC:
35  case BERNSTEIN:
36  case SZABAB:
37  case CLOUGH: // PB: Really H2
38  case HERMITE: // PB: Really H2
39  case SUBDIVISION:
40  case LAGRANGE_VEC:
41  case MONOMIAL: // PB: Shouldn't this be L2 conforming?
42  case XYZ: // PB: Shouldn't this be L2 conforming?
43  case L2_HIERARCHIC: // PB: Shouldn't this be L2 conforming?
44  case L2_LAGRANGE: // PB: Shouldn't this be L2 conforming?
45  case JACOBI_20_00: // PB: For infinite elements...
46  case JACOBI_30_00: // PB: For infinite elements...
47  return libmesh_make_unique<H1FETransformation<OutputShape>>();
48 
49  // HCurl Conforming Elements
50  case NEDELEC_ONE:
51  return libmesh_make_unique<HCurlFETransformation<OutputShape>>();
52 
53  // HDiv Conforming Elements
54  // L2 Conforming Elements
55 
56  // Other...
57  case SCALAR:
58  // Should never need this for SCALARs
59  return libmesh_make_unique<H1FETransformation<OutputShape>>();
60 
61  default:
62  libmesh_error_msg("Unknown family = " << fe_type.family);
63  }
64 }

◆ init_map_d2phi() [1/2]

template<typename OutputShape >
void libMesh::HCurlFETransformation< OutputShape >::init_map_d2phi ( const FEGenericBase< OutputShape > &  fe) const
overridevirtual

Pre-requests any necessary data from FEMap

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 42 of file hcurl_fe_transformation.C.

References libMesh::FEMap::get_d2xidxyz2(), libMesh::FEMap::get_dxidx(), and libMesh::FEAbstract::get_fe_map().

43 {
44  fe.get_fe_map().get_dxidx();
45 #ifdef LIBMESH_ENABLE_SECOND_DERIVATIVES
46  fe.get_fe_map().get_d2xidxyz2();
47 #endif
48 }

◆ init_map_d2phi() [2/2]

template<>
void libMesh::HCurlFETransformation< Real >::init_map_d2phi ( const FEGenericBase< Real > &  ) const

Definition at line 267 of file hcurl_fe_transformation.C.

268 {
269  libmesh_error_msg("HCurl transformations only make sense for vector-valued elements.");
270 }

◆ init_map_dphi() [1/2]

template<typename OutputShape >
void libMesh::HCurlFETransformation< OutputShape >::init_map_dphi ( const FEGenericBase< OutputShape > &  fe) const
overridevirtual

Pre-requests any necessary data from FEMap

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 34 of file hcurl_fe_transformation.C.

References libMesh::FEMap::get_dxidx(), and libMesh::FEAbstract::get_fe_map().

35 {
36  fe.get_fe_map().get_dxidx();
37 }

◆ init_map_dphi() [2/2]

template<>
void libMesh::HCurlFETransformation< Real >::init_map_dphi ( const FEGenericBase< Real > &  ) const

Definition at line 261 of file hcurl_fe_transformation.C.

262 {
263  libmesh_error_msg("HCurl transformations only make sense for vector-valued elements.");
264 }

◆ init_map_phi() [1/2]

template<typename OutputShape >
void libMesh::HCurlFETransformation< OutputShape >::init_map_phi ( const FEGenericBase< OutputShape > &  fe) const
overridevirtual

Pre-requests any necessary data from FEMap

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 26 of file hcurl_fe_transformation.C.

References libMesh::FEMap::get_dxidx(), and libMesh::FEAbstract::get_fe_map().

27 {
28  fe.get_fe_map().get_dxidx();
29 }

◆ init_map_phi() [2/2]

template<>
void libMesh::HCurlFETransformation< Real >::init_map_phi ( const FEGenericBase< Real > &  ) const

Definition at line 255 of file hcurl_fe_transformation.C.

256 {
257  libmesh_error_msg("HCurl transformations only make sense for vector-valued elements.");
258 }

◆ map_curl() [1/2]

template<typename OutputShape >
void libMesh::HCurlFETransformation< OutputShape >::map_curl ( const unsigned int  dim,
const Elem *const  elem,
const std::vector< Point > &  qp,
const FEGenericBase< OutputShape > &  fe,
std::vector< std::vector< OutputShape >> &  curl_phi 
) const
overridevirtual

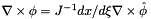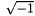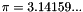Evaluates the shape function curl in physical coordinates based on $ H(curl) $ conforming finite element transformation. In 2-D, the transformation is $ \nabla \times \phi = J^{-1} * \nabla \times \hat{\phi} $ where $ J = \det( dx/d\xi ) $ In 3-D, the transformation is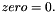 $ \nabla \times \phi = J^{-1} dx/d\xi \nabla \times \hat{\phi} $

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 152 of file hcurl_fe_transformation.C.

References libMesh::FEGenericBase< OutputType >::get_dphideta(), libMesh::FEGenericBase< OutputType >::get_dphidxi(), libMesh::FEGenericBase< OutputType >::get_dphidzeta(), libMesh::FEMap::get_dxyzdeta(), libMesh::FEMap::get_dxyzdxi(), libMesh::FEMap::get_dxyzdzeta(), libMesh::FEAbstract::get_fe_map(), libMesh::FEMap::get_jacobian(), libMesh::index_range(), and libMesh::Real.

157 {
158  switch (dim)
159  {
160  case 0:
161  case 1:
162  libmesh_error_msg("These element transformations only make sense in 2D and 3D.");
163 
164  case 2:
165  {
166  const std::vector<std::vector<OutputShape>> & dphi_dxi = fe.get_dphidxi();
167  const std::vector<std::vector<OutputShape>> & dphi_deta = fe.get_dphideta();
168 
169  const std::vector<Real> & J = fe.get_fe_map().get_jacobian();
170 
171  // FIXME: I don't think this is valid for 2D elements in 3D space
172  // In 2D: curl(phi) = J^{-1} * curl(\hat{phi})
173  for (auto i : index_range(curl_phi))
174  for (auto p : index_range(curl_phi[i]))
175  {
176  curl_phi[i][p].slice(0) = curl_phi[i][p].slice(1) = 0.0;
177  curl_phi[i][p].slice(2) = ( dphi_dxi[i][p].slice(1) - dphi_deta[i][p].slice(0) )/J[p];
178  }
179 
180  break;
181  }
182 
183  case 3:
184  {
185  const std::vector<std::vector<OutputShape>> & dphi_dxi = fe.get_dphidxi();
186  const std::vector<std::vector<OutputShape>> & dphi_deta = fe.get_dphideta();
187  const std::vector<std::vector<OutputShape>> & dphi_dzeta = fe.get_dphidzeta();
188 
189  const std::vector<RealGradient> & dxyz_dxi = fe.get_fe_map().get_dxyzdxi();
190  const std::vector<RealGradient> & dxyz_deta = fe.get_fe_map().get_dxyzdeta();
191  const std::vector<RealGradient> & dxyz_dzeta = fe.get_fe_map().get_dxyzdzeta();
192 
193  const std::vector<Real> & J = fe.get_fe_map().get_jacobian();
194 
195  for (auto i : index_range(curl_phi))
196  for (auto p : index_range(curl_phi[i]))
197  {
198  Real dx_dxi = dxyz_dxi[p](0);
199  Real dx_deta = dxyz_deta[p](0);
200  Real dx_dzeta = dxyz_dzeta[p](0);
201 
202  Real dy_dxi = dxyz_dxi[p](1);
203  Real dy_deta = dxyz_deta[p](1);
204  Real dy_dzeta = dxyz_dzeta[p](1);
205 
206  Real dz_dxi = dxyz_dxi[p](2);
207  Real dz_deta = dxyz_deta[p](2);
208  Real dz_dzeta = dxyz_dzeta[p](2);
209 
210  const Real inv_jac = 1.0/J[p];
211 
212  /* In 3D: curl(phi) = J^{-1} dx/dxi * curl(\hat{phi})
213 
214  dx/dxi = [ dx/dxi dx/deta dx/dzeta
215  dy/dxi dy/deta dy/dzeta
216  dz/dxi dz/deta dz/dzeta ]
217 
218  curl(u) = [ du_z/deta - du_y/dzeta
219  du_x/dzeta - du_z/dxi
220  du_y/dxi - du_x/deta ]
221  */
222  curl_phi[i][p].slice(0) = inv_jac*( dx_dxi*( dphi_deta[i][p].slice(2) -
223  dphi_dzeta[i][p].slice(1) ) +
224  dx_deta*( dphi_dzeta[i][p].slice(0) -
225  dphi_dxi[i][p].slice(2) ) +
226  dx_dzeta*( dphi_dxi[i][p].slice(1) -
227  dphi_deta[i][p].slice(0) ) );
228 
229  curl_phi[i][p].slice(1) = inv_jac*( dy_dxi*( dphi_deta[i][p].slice(2) -
230  dphi_dzeta[i][p].slice(1) ) +
231  dy_deta*( dphi_dzeta[i][p].slice(0)-
232  dphi_dxi[i][p].slice(2) ) +
233  dy_dzeta*( dphi_dxi[i][p].slice(1) -
234  dphi_deta[i][p].slice(0) ) );
235 
236  curl_phi[i][p].slice(2) = inv_jac*( dz_dxi*( dphi_deta[i][p].slice(2) -
237  dphi_dzeta[i][p].slice(1) ) +
238  dz_deta*( dphi_dzeta[i][p].slice(0) -
239  dphi_dxi[i][p].slice(2) ) +
240  dz_dzeta*( dphi_dxi[i][p].slice(1) -
241  dphi_deta[i][p].slice(0) ) );
242  }
243 
244  break;
245  }
246 
247  default:
248  libmesh_error_msg("Invalid dim = " << dim);
249  } // switch(dim)
250 }
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104
libMesh::Real
DIE A HORRIBLE DEATH HERE typedef LIBMESH_DEFAULT_SCALAR_TYPE Real
Definition: libmesh_common.h:131

◆ map_curl() [2/2]

template<>
void libMesh::HCurlFETransformation< Real >::map_curl ( const unsigned int  ,
const Elem *  const,
const std::vector< Point > &  ,
const FEGenericBase< Real > &  ,
std::vector< std::vector< Real >> &   
) const

Definition at line 283 of file hcurl_fe_transformation.C.

288 {
289  libmesh_error_msg("HCurl transformations only make sense for vector-valued elements.");
290 }

◆ map_d2phi()

template<typename OutputShape >
virtual void libMesh::HCurlFETransformation< OutputShape >::map_d2phi ( const unsigned int  ,
const std::vector< Point > &  ,
const FEGenericBase< OutputShape > &  ,
std::vector< std::vector< typename FEGenericBase< OutputShape >::OutputTensor >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &   
) const
inlineoverridevirtual

Evaluates shape function Hessians in physical coordinates based on 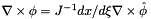$ H(curl) $ conforming finite element transformation.

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 95 of file hcurl_fe_transformation.h.

105  {
106  libmesh_warning("WARNING: Shape function Hessians for HCurl elements are not currently being computed!");
107  }

◆ map_div()

template<typename OutputShape >
virtual void libMesh::HCurlFETransformation< OutputShape >::map_div ( const unsigned int  ,
const Elem *  const,
const std::vector< Point > &  ,
const FEGenericBase< OutputShape > &  ,
std::vector< std::vector< typename FEGenericBase< OutputShape >::OutputDivergence >> &   
) const
inlineoverridevirtual

Evaluates the shape function divergence in physical coordinates based on 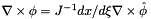$ H(curl) $ conforming finite element transformation.

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 127 of file hcurl_fe_transformation.h.

132  {
133  libmesh_warning("WARNING: Shape function divergences for HCurl elements are not currently being computed!");
134  }

◆ map_dphi()

template<typename OutputShape >
virtual void libMesh::HCurlFETransformation< OutputShape >::map_dphi ( const unsigned int  ,
const Elem *  const,
const std::vector< Point > &  ,
const FEGenericBase< OutputShape > &  ,
std::vector< std::vector< typename FEGenericBase< OutputShape >::OutputGradient >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &  ,
std::vector< std::vector< OutputShape >> &   
) const
inlineoverridevirtual

Evaluates shape function gradients in physical coordinates for 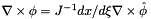$ H(curl) $ conforming elements.

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 78 of file hcurl_fe_transformation.h.

86  {
87  libmesh_warning("WARNING: Shape function gradients for HCurl elements are not currently being computed!");
88  }

◆ map_phi() [1/2]

template<typename OutputShape >
void libMesh::HCurlFETransformation< OutputShape >::map_phi ( const unsigned int  dim,
const Elem *const  elem,
const std::vector< Point > &  qp,
const FEGenericBase< OutputShape > &  fe,
std::vector< std::vector< OutputShape >> &  phi 
) const
overridevirtual

Evaluates shape functions in physical coordinates for 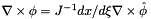$ H(curl) $ conforming elements. In this case 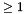$ \phi = (dx/d\xi)^{-T} \hat{\phi} $, where 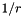$ (dx/d\xi)^{-T} $ is the inverse-transpose of the Jacobian matrix of the element map.

Note
Here 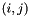$ x, \xi $ are vectors.

Implements libMesh::FETransformationBase< OutputShape >.

Definition at line 53 of file hcurl_fe_transformation.C.

References libMesh::FEMap::get_detadx(), libMesh::FEMap::get_detady(), libMesh::FEMap::get_detadz(), libMesh::FEMap::get_dxidx(), libMesh::FEMap::get_dxidy(), libMesh::FEMap::get_dxidz(), libMesh::FEMap::get_dzetadx(), libMesh::FEMap::get_dzetady(), libMesh::FEMap::get_dzetadz(), libMesh::FEAbstract::get_fe_map(), libMesh::FEAbstract::get_fe_type(), and libMesh::index_range().

58 {
59  switch (dim)
60  {
61  case 0:
62  case 1:
63  libmesh_error_msg("These element transformations only make sense in 2D and 3D.");
64 
65  case 2:
66  {
67  const std::vector<Real> & dxidx_map = fe.get_fe_map().get_dxidx();
68  const std::vector<Real> & dxidy_map = fe.get_fe_map().get_dxidy();
69 
70  const std::vector<Real> & detadx_map = fe.get_fe_map().get_detadx();
71  const std::vector<Real> & detady_map = fe.get_fe_map().get_detady();
72 
73  // FIXME: Need to update for 2D elements in 3D space
74  // phi = (dx/dxi)^-T * \hat{phi}
75  // In 2D:
76  // (dx/dxi)^{-1} = [ dxi/dx dxi/dy
77  // deta/dx deta/dy ]
78  //
79  // so: dxi/dx^{-T} * \hat{phi} = [ dxi/dx deta/dx [ \hat{phi}_xi
80  // dxi/dy deta/dy ] \hat{phi}_eta ]
81  //
82  // or in indicial notation: phi_j = xi_{i,j}*\hat{phi}_i
83  for (auto i : index_range(phi))
84  for (auto p : index_range(phi[i]))
85  {
86  // Need to temporarily cache reference shape functions
87  // TODO: PB: Might be worth trying to build phi_ref separately to see
88  // if we can get vectorization
89  OutputShape phi_ref;
90  FEInterface::shape<OutputShape>(2, fe.get_fe_type(), elem, i, qp[p], phi_ref);
91 
92  phi[i][p](0) = dxidx_map[p]*phi_ref.slice(0) + detadx_map[p]*phi_ref.slice(1);
93 
94  phi[i][p](1) = dxidy_map[p]*phi_ref.slice(0) + detady_map[p]*phi_ref.slice(1);
95  }
96 
97  break;
98  }
99 
100  case 3:
101  {
102  const std::vector<Real> & dxidx_map = fe.get_fe_map().get_dxidx();
103  const std::vector<Real> & dxidy_map = fe.get_fe_map().get_dxidy();
104  const std::vector<Real> & dxidz_map = fe.get_fe_map().get_dxidz();
105 
106  const std::vector<Real> & detadx_map = fe.get_fe_map().get_detadx();
107  const std::vector<Real> & detady_map = fe.get_fe_map().get_detady();
108  const std::vector<Real> & detadz_map = fe.get_fe_map().get_detadz();
109 
110  const std::vector<Real> & dzetadx_map = fe.get_fe_map().get_dzetadx();
111  const std::vector<Real> & dzetady_map = fe.get_fe_map().get_dzetady();
112  const std::vector<Real> & dzetadz_map = fe.get_fe_map().get_dzetadz();
113 
114  // phi = (dx/dxi)^-T * \hat{phi}
115  // In 3D:
116  // dx/dxi^-1 = [ dxi/dx dxi/dy dxi/dz
117  // deta/dx deta/dy deta/dz
118  // dzeta/dx dzeta/dy dzeta/dz]
119  //
120  // so: dxi/dx^-T * \hat{phi} = [ dxi/dx deta/dx dzeta/dx [ \hat{phi}_xi
121  // dxi/dy deta/dy dzeta/dy \hat{phi}_eta
122  // dxi/dz deta/dz dzeta/dz ] \hat{phi}_zeta ]
123  //
124  // or in indicial notation: phi_j = xi_{i,j}*\hat{phi}_i
125  for (auto i : index_range(phi))
126  for (auto p : index_range(phi[i]))
127  {
128  // Need to temporarily cache reference shape functions
129  // TODO: PB: Might be worth trying to build phi_ref separately to see
130  // if we can get vectorization
131  OutputShape phi_ref;
132  FEInterface::shape<OutputShape>(3, fe.get_fe_type(), elem, i, qp[p], phi_ref);
133 
134  phi[i][p].slice(0) = dxidx_map[p]*phi_ref.slice(0) + detadx_map[p]*phi_ref.slice(1)
135  + dzetadx_map[p]*phi_ref.slice(2);
136 
137  phi[i][p].slice(1) = dxidy_map[p]*phi_ref.slice(0) + detady_map[p]*phi_ref.slice(1)
138  + dzetady_map[p]*phi_ref.slice(2);
139 
140  phi[i][p].slice(2) = dxidz_map[p]*phi_ref.slice(0) + detadz_map[p]*phi_ref.slice(1)
141  + dzetadz_map[p]*phi_ref.slice(2);
142  }
143  break;
144  }
145 
146  default:
147  libmesh_error_msg("Invalid dim = " << dim);
148  } // switch(dim)
149 }
libMesh::index_range
IntRange< std::size_t > index_range(const std::vector< T > &vec)
Definition: int_range.h:104

◆ map_phi() [2/2]

template<>
void libMesh::HCurlFETransformation< Real >::map_phi ( const unsigned int  ,
const Elem *  const,
const std::vector< Point > &  ,
const FEGenericBase< Real > &  ,
std::vector< std::vector< Real >> &   
) const

Definition at line 273 of file hcurl_fe_transformation.C.

278 {
279  libmesh_error_msg("HCurl transformations only make sense for vector-valued elements.");
280 }
The documentation for this class was generated from the following files:
generated by doxygen